資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究已知\( \mathrm{ABC} \) 是一個直角三角形，\( \mathrm{C} \) 為直角頂點。過斜邊\( \mathrm{AB} \) 的中點\( \mathrm{M} \) 且平行於\( \mathrm{BC} \) 的直線交\( \mathrm{AC} \) 於\( \mathrm{D} \)。證明：
(i) \( \mathrm{D} \) 是\( \mathrm{AC} \) 的中點
(ii) \( \mathrm{MD} \perp \mathrm{AC} \)
(iii) \( \mathrm{CM}=\mathrm{MA}=\frac{1}{2} \mathrm{AB} \)
已知
\( \mathrm{ABC} \) 是一個直角三角形，\( \mathrm{C} \) 為直角頂點。過斜邊\( \mathrm{AB} \) 的中點\( \mathrm{M} \) 且平行於\( \mathrm{BC} \) 的直線交\( \mathrm{AC} \) 於\( \mathrm{D} \)。
求證：
我們需要證明：
(i) \( \mathrm{D} \) 是\( \mathrm{AC} \) 的中點
(ii) \( \mathrm{MD} \perp \mathrm{AC} \)
(iii) \( \mathrm{CM}=\mathrm{MA}=\frac{1}{2} \mathrm{AB} \)
解答
\( \mathrm{ABC} \) 是一個直角三角形，\( \mathrm{C} \) 為直角頂點。
這意味著：
$\angle C=90^o$
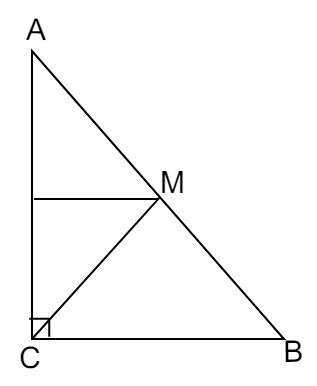
$M$ 是斜邊 $AB$ 的中點。
$DM \| BC$
(i) 在 $\triangle \mathrm{ABC}$ 中，
$\mathrm{BC} \| \mathrm{MD}$
$\mathrm{M}$ 是 $\mathrm{AB}$ 的中點。
因此，根據中點定理的逆定理，我們得到：
$D$ 是 $AC$ 的中點。
(ii) $MD \| B C$ 且 $C D$ 是橫截線。
這意味著：
$\angle A D M=\angle A C B=90^{\circ}$ (同位角相等)
$\Rightarrow \mathrm{MD} \perp \mathrm{AC}$
(iii) 在 $\triangle A D M$ 和 $\triangle C D M$ 中，
$\mathrm{DM}=\mathrm{DM}$ (公共邊)
$AD=C D$ ($D$ 是 $AC$ 的中點)
$\angle \mathrm{ADM}=\angle \mathrm{MDC} = 90^{\circ}$
因此，根據 SAS 全等定理，我們得到：
$\triangle \mathrm{ADM}=\triangle \mathrm{CDM}$
這意味著：
$\mathrm{CM}=\mathrm{AM}$ (全等三角形對應邊相等)......(i)
$M$ 是 $AB$ 的中點。
$\mathrm{AM}=\mathrm{BM}=\frac{1}{2} \mathrm{AB}$.......(ii)
由 (i) 和 (ii) 可得：
$\mathrm{CM}=\mathrm{AM}=\frac{1}{2} \mathrm{AB}$
證畢。
60 次瀏覽
