資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究從一座高 \( h \) 米的塔頂，觀察到與塔底在同一直線上的兩個物體的俯角分別為 \( \alpha \) 和 \( \beta(\beta>\alpha) \)。求這兩個物體之間的距離。
已知
從一座高 \( h \) 米的塔頂，觀察到與塔底在同一直線上的兩個物體的俯角分別為 \( \alpha \) 和 \( \beta(\beta>\alpha) \)。
求解
我們需要求出這兩個物體之間的距離。
解題步驟
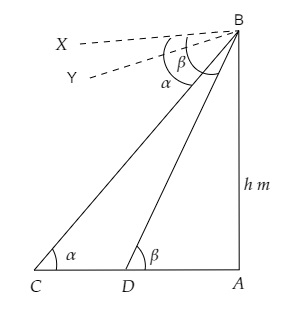
設這兩個物體之間的距離為 $x\ 米$，$DA= y\ 米$，塔高為 $AB = h\ 米$。
根據圖形，
$\angle XBC=\angle BCA = \alpha$ (內錯角相等)
$\angle XBD = \angle BDA = \beta$ (內錯角相等)
在 $\Delta \mathrm{ABD}$ 中，
$\tan \beta=\frac{\mathrm{AB}}{\mathrm{AD}}$
$=\frac{h}{y}$
$\Rightarrow y=\frac{h}{\tan \beta}$.............(i)
在 $\Delta \mathrm{BCA}$ 中，
$\tan \alpha=\frac{\mathrm{AB}}{\mathrm{AC}}$
$\Rightarrow \tan \alpha=\frac{\mathrm{AB}}{\mathrm{CD}+\mathrm{AD}}$
$\Rightarrow \tan \alpha=\frac{h}{x+y}$
$\Rightarrow x+y=\frac{h}{\tan \alpha}$
$\Rightarrow y=\frac{h}{\tan \alpha}-x$............(ii)
由公式 (i) 和 (ii)，
$\frac{h}{\tan \beta}=\frac{h}{\tan \alpha}-x$
$x=\frac{h}{\tan \alpha}-\frac{h}{\tan \beta}$
$x=h(\frac{1}{\tan \alpha}-\frac{1}{\tan \beta})$
$x=h(\cot \alpha-\cot \beta)$
因此，這兩個物體之間的距離為 $h(\cot \alpha-\cot \beta)$。
80 次瀏覽
