資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究從山頂上，觀察到正東方向的兩塊相鄰的千米路標的俯角分別為 \( 30^{\circ} \) 和 \( 45^{\circ} \)。求這兩塊路標到山腳的距離。
已知
從山頂上，觀察到兩個連續千米路標的俯角為
45°和 30°
求：
這兩塊路標到山腳的距離。
解
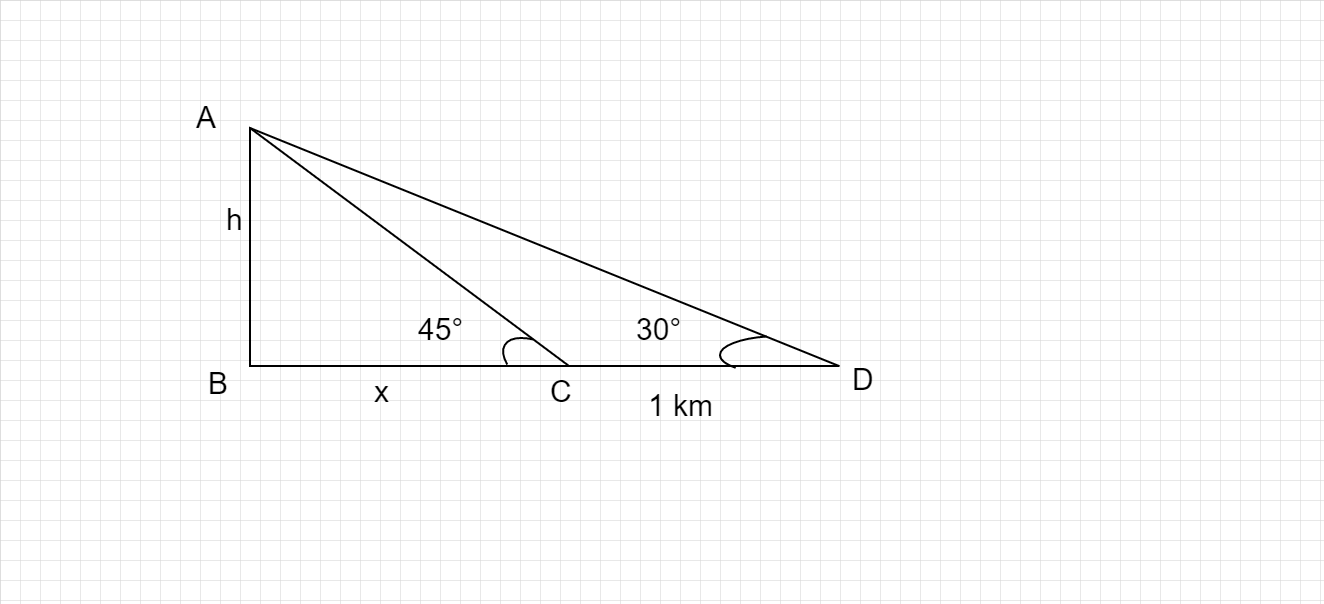
山高 AB = h
距離 BC = x km
距離 CD = 1 km
在 ABC 中 $$\displaystyle tan\ \theta \ =\ \frac{對邊}{鄰邊} \ $$
$$\displaystyle tan\ 45=\ \frac{h}{x} \ $$ (tan 45° = 1)
$$\displaystyle 1\ =\ \frac{h}{x}$$
h = x .....................................................(i)
在 ABD 中
$$\displaystyle tan\ 30\ =\ \frac{h}{x\ +\ 1} \ $$
$$\displaystyle \frac{1}{\sqrt{3}} \ =\ \frac{h}{x\ +\ 1} \ $$
交叉相乘，
$$\displaystyle x\ +\ 1\ =\ \sqrt{3} h$$
改寫，
$$\displaystyle \ \sqrt{3} h\ =\ x\ +\ 1\ ...........................................( ii)$$
將 (i) 代入 (ii)
$$\displaystyle \ \sqrt{3} \ x\ =\ x\ +\ 1\ $$
$$\displaystyle \ \sqrt{3} \ x\ -\ x\ =\ 1\ $$
提取 x 為公因數，
$$\displaystyle x\ \left(\sqrt{3} \ -\ 1\right) \ =\ 1$$
$$\displaystyle x\ =\ \frac{1}{\sqrt{3} \ -\ 1}$$
取共軛，
$$\displaystyle x\ =\ \frac{1}{\sqrt{3} \ -\ 1} \ \times \frac{\sqrt{3} \ +\ 1}{\sqrt{3} \ +\ 1}$$
$$\displaystyle x\ =\ \frac{\sqrt{3} \ +\ 1}{\left(\sqrt{3} \ \ \right)^{2} -\ ( 1)^{2}}$$
$$\displaystyle x\ =\ \frac{\sqrt{3} \ +\ 1}{3\ -\ 1}$$
$$\displaystyle x\ =\ \frac{\sqrt{3} \ +\ 1}{2}$$
√3 = 1.732
$$\displaystyle x\ =\ \frac{\ 1.732+\ 1}{2}$$
$$\displaystyle x\ =\ \frac{\ 2.732}{2}$$
x = 1.366
距離 BC = 1.366 km
第一個路標到山腳的距離 = 1.366 km
第二個路標到山腳的距離
$$\displaystyle BD\ =\ BC\ +\ CD$$
$$\displaystyle BD\ =\ 1.366\ +\ 1$$
距離 = 2.366 km
第二個路標到山腳的距離 = 2.366 km
99 次檢視
