資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法學從一棟高 AB = 60 米的建築物頂部，觀察到垂直燈柱 CD 的頂部和底部的俯角分別為 30° 和 60°。求 AB 和 CD 之間的水平距離。
已知
從一棟高 AB = 60 米的建築物頂部，觀察到垂直燈柱 CD 的頂部和底部的俯角分別為 30° 和 60°。
要求
我們必須求出 AB 和 CD 之間的水平距離。
解答：
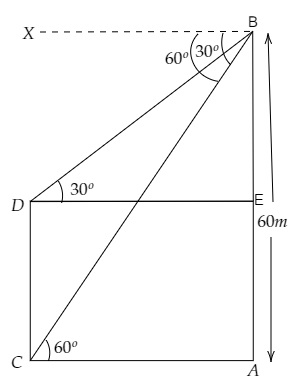
根據圖示：
AB=60 m, ∠BDE=30°, ∠BCA=60°
設 AB 和 CD 之間的水平距離為 AC=x m，燈柱的高度為 CD=h m。
這意味著：
AE=CD=h m
DE=CA=x m
BE=60-h m
我們知道：
tan θ = 對邊 / 鄰邊
= BE / DE
=> tan 30° = (60-h) / x
=> 1/√3 = (60-h) / x
=> x = (60-h)√3 m ............(i)
類似地：
tan θ = 對邊 / 鄰邊
= AB / CA
=> tan 60° = 60 / x
=> √3 = 60 / [(60-h)√3] [根據 (i)]
=> (60-h)√3 * √3 = 60 m
=> (60-h) * 3 = 60 m
=> 60-h = 20 m
=> h = 60-20 m
=> h = 40 m
=> x = (60-40) * 1.73 = 20 * 1.73 = 34.64 m
因此，AB 和 CD 之間的水平距離為34.64 m。
更新於：2022年10月10日
瀏覽量：128
廣告