資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究求頂點座標為$(-4, -2), (-3, -5), (3, -2), (2, 3)$的四邊形的面積。
已知
四邊形的頂點為$(-4, -2), (-3, -5), (3, -2), (2, 3)$。
要求
我們需要求出四邊形的面積。
解答
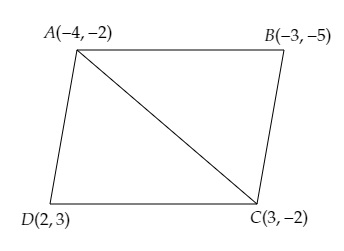
設四邊形$ABCD$的頂點分別為$A (-4, -2), B (-3, -5), C(3,-2)$ 和 $D (2, 3)$。
連線$A$和$C$，將四邊形分成兩個三角形$ABC$和$ADC$。
這意味著，
四邊形$ABCD$的面積 = 三角形$ABC$的面積 + 三角形$ADC$的面積。
我們知道，
頂點為$(x_1,y_1), (x_2,y_2), (x_3,y_3)$的三角形的面積由以下公式給出：
三角形面積$\Delta=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$
因此，
三角形\( ABC\)的面積\(=\frac{1}{2}[-4(-5+2)+(-3)(-2+2)+3(-2+5)] \)
\( =\frac{1}{2}[-4(-3)+(-3)0+3(3)] \)
\( =\frac{1}{2}[12+9] \)
\( =\frac{1}{2} \times 21 \)
\( =\frac{21}{2} \) 平方單位。
三角形\( ADC\)的面積\(=\frac{1}{2}[-4(-2-3)+2(-2+2)+3(3+2)] \)
\( =\frac{1}{2}[-4(-5)+2(0)+3(5)] \)
\( =\frac{1}{2}[20+0+15] \)
\( =\frac{1}{2} \times 35 \)
\( =\frac{35}{2} \) 平方單位。
因此，
四邊形$ABCD$的面積 = $\frac{21}{2}+\frac{35}{2}=\frac{21+35}{2}=\frac{56}{2}=28$ 平方單位。
給定四邊形的面積為$28$ 平方單位。
49 次瀏覽
