資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝學
法學一座垂直塔矗立在水平面上，塔頂上豎立著一根高度為 $h$ 的旗杆。在平面上的一個點，旗杆底部和頂部的仰角分別為 $\alpha$ 和 $\beta$。求塔的高度。
已知：一座垂直塔矗立在水平面上，塔頂上豎立著一根高度為 $h$ 的垂直旗杆。在平面上的一個點，旗杆底部和頂部的仰角分別為 $\alpha$ 和 $\beta$。
求解：求塔的高度。
解
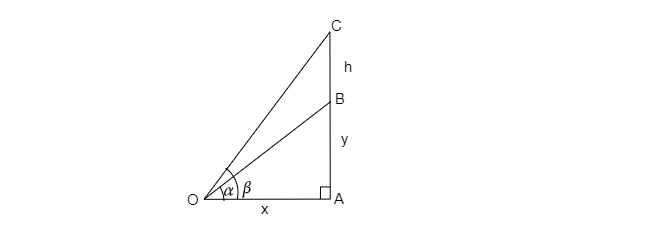
設塔高為 $y$，$\vartriangle OAC$
$tan\beta =\frac{CA}{OA}$
$tan\beta =\frac{y+h}{x}$ $(y+h)=CA=AB+BC,\ 設 OA=x$
$x=( \frac{y+h}{tan\beta})$
考慮 $\vartriangle OAB$
$tan\alpha =\frac{y}{x}$
$x=\frac{y}{tan\alpha }$
$\frac{y}{tan\alpha }=\frac{y+h}{tan\beta}$
$y.tan\beta =y.tan\alpha +h.tan\alpha $
$y.tan\beta −y.tan\alpha=h.tan\alpha $
$y(tan\beta −tan\alpha )=h.tan\alpha $
$y=\frac{h.tan\alpha}{tan\beta −tan\alpha }$
更新於： 2022年10月10日
82 次瀏覽
廣告