一列火車下午2點離開城市。第二列火車下午4點離開城市，並以比第一列火車快32公里/小時的速度追趕第一列火車。如果第二列火車在晚上8點追上第一列火車，求兩列火車的速度。

已知：一列火車下午$2:00$離開城市。第二列火車下午$4:00$離開城市，並以比第一列火車快$32\ km/h$的速度追趕第一列火車。如果第二列火車在晚上$8:00$追上第一列火車。

求解：求兩列火車的速度。

解答

設$A$和$B$分別為第一列和第二列火車。設第一列火車$A$的速度為$x\ km/hr$，則第二列火車$B$的速度為$( x+32)\ km/hr$。

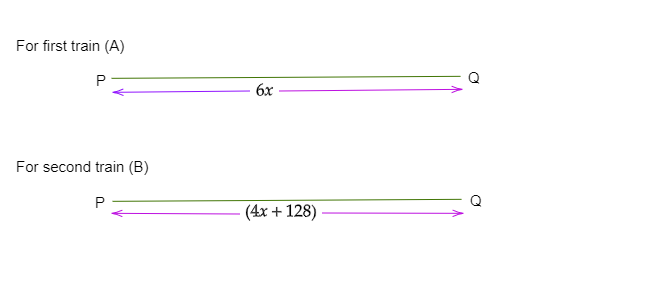
晚上$8:00$，第二列火車追上了第一列火車。

第一列火車行駛時間$=6\ hr$

第二列火車行駛時間$=4\ hr$

第一列火車$( A)$行駛距離$=PQ=速度\times 時間=x\times 6=6x$

第二列火車$( B)$行駛距離$=PQ=速度\times 時間=( x+32) \times 4=4(x+32)$

因為兩列火車行駛距離相同。

$\Rightarrow 6x=4(x+32)$

$\Rightarrow 6x=4x+128$

$\Rightarrow 6x-4x=128$

$\Rightarrow 2x=128$

$\Rightarrow x=\frac{128}{2}$

$\Rightarrow x=64$

因此，第一列火車的速度$=x=64\ km/hr$

第二列火車的速度$=x+32=64+32=96\ km/hr$

教程點

更新於：2022年10月10日

瀏覽量600次

開啟您的職業生涯

完成課程獲得認證

開始學習