資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究一個實心直圓錐體被一個平行於底面的平面在它高度的中點處切成兩部分。求小圓錐體積與整個圓錐體積的比值。
已知：一個實心直圓錐體被一個平行於底面的平面在它高度的中點處切成兩部分。
要求：求小圓錐體積與整個圓錐體積的比值。
解答
設給定圓錐體的半徑為 $r$，高為 $h$。
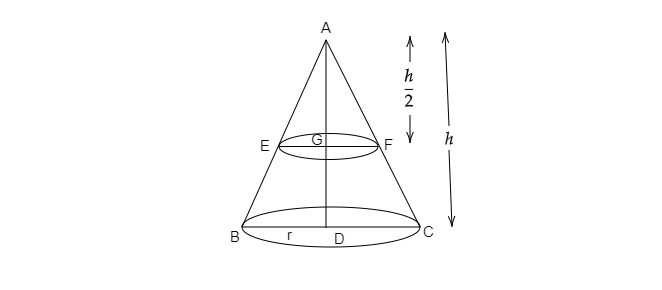
$AD=h$ 且 $DC=r$
$\therefore AG=\frac{h}{2}$
在 $\vartriangle AGF$ 和 $\vartriangle ADC$ 中
$\angle AFG=\angle ACD$
$\because EF||BC$
$\therefore \angle AGE=\angle ADC=90^o$
$\vartriangle AGF\sim \vartriangle ADC$
$\Rightarrow \frac{AG}{AD}=\frac{GF}{DC}$
$\Rightarrow \frac{\frac{h}{2}}{h}=\frac{GF}{DC}$
$\Rightarrow \frac{GF}{DC}=\frac{1}{2}$
$\Rightarrow \frac{GF}{r}=\frac{1}{2}$
$\Rightarrow GF=\frac{r}{2}$
$\Rightarrow \frac{小圓錐體積}{整個圓錐體積}=\frac{\frac{1}{3}\times \pi\ ( \frac{r}{2})^2\times( \frac{h}{2})}{\frac{1}{3}\times \pi r^2h}$
$=\frac{1}{8}$
$=1:8$
因此，小圓錐體積與整個圓錐體積的比值為 $1:8$。
更新於: 2022年10月10日
535 次瀏覽
廣告