資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學一個高20釐米，頂角為60°的金屬直圓錐，在其高度一半處被一個平行於底面的平面切成兩部分。如果由此得到的圓臺被拉成直徑為$\frac{1}{16}$釐米的金屬絲，求金屬絲的長度。
已知
一個高20釐米，頂角為$60^{o}$的金屬直圓錐，在其高度一半處被一個平行於底面的平面切成兩部分。
由此得到的圓臺被拉成直徑為$\frac{1}{16}$釐米的金屬絲。
要求
求金屬絲的長度。
解答
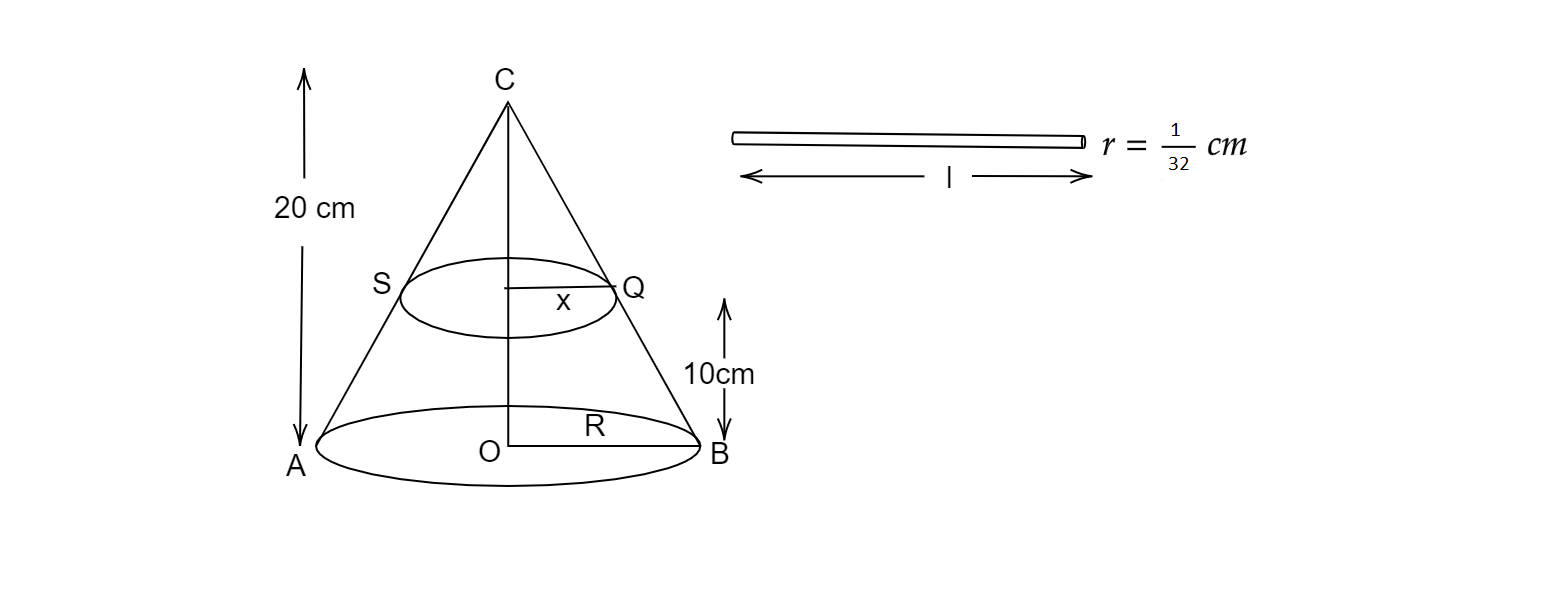
設ACB為圓錐，其頂角$\angle ACB = 60^{o} $。
設$R$和$x$分別為圓臺上下底的半徑。
圓錐高$OC = 20 cm=H$
高$CP = h = 10\ cm $
設P為OC的中點
透過P將圓錐切成兩部分。
OP =$\frac{20}{2}= 10\ cm$
且$\angle ACO$ 和 $\angle OCB =\frac{1}{2} \times 60^{o} =30^{o} $
從圓錐CBA切下圓錐CQS後，剩餘部分為圓臺。
在三角形CPQ中
$tan30^{o}=\frac{x}{10}$
$\frac{1}{\sqrt{3}} =\frac{x}{10}$
$\Rightarrow x=\frac{10}{\sqrt{3}}\ cm$
在三角形COB中
$tan30^{o}=\frac{R}{20}$
$\Rightarrow \frac{1}{\sqrt{3}} =\frac{R}{20}$
$\Rightarrow R=\frac{20}{\sqrt{3}}$
圓臺體積，$V=\frac{1}{3} \pi \left( R^{2} H-x^{2} h\right)$
$\Rightarrow V=\frac{1}{3} \pi \left(\left(\frac{20}{\sqrt{3}}\right)^{2} .20-\left(\frac{10}{\sqrt{3}}\right)^{2} .10\right)$
$\Rightarrow V=\frac{1}{3} \pi \left(\frac{400\times 20}{3} -\frac{100\times 10}{3}\right)$
$\Rightarrow V=\frac{1}{3} \pi \left(\frac{8000-1000}{3}\right)$
$\Rightarrow V=\frac{7000}{9} \pi \ cm^{3}$
設金屬絲長度為$l$。
已知金屬絲直徑為$\frac{1}{16}\ cm$
金屬絲半徑，$r=\frac{1}{2} \times \frac{1}{16} =\frac{1}{32}\ cm$
金屬絲體積$=\pi r^{2} l$
$=\pi \left(\frac{1}{32}\right)^{2} l$
$=\frac{\pi l}{1024} cm^{3}$
圓臺和金屬絲的體積相等，
$\frac{7000}{9} \pi =\frac{\pi l}{1024}$
$\Rightarrow \frac{7000}{9} =\frac{l}{1024}$
$\Rightarrow l=\frac{7000\times 1024}{9}$
$\Rightarrow l=796444.44\ cm$
$\Rightarrow l=7964.44\ m$
因此，金屬絲的長度為7964.4米。
65次瀏覽
