資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究一個底面半徑為 \( 10 \mathrm{~cm} \) 的實心圓錐，被一個平行於底面的平面沿其高度中點截成兩部分。求圓錐兩部分體積的比值。
已知
一個底面半徑為 \( 10 \mathrm{~cm} \) 的實心圓錐，被一個平行於底面的平面沿其高度中點截成兩部分。
要求
我們需要求圓錐兩部分體積的比值。
解答
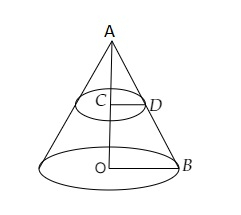
實心圓錐底面半徑 $r = 10\ cm$
設圓錐的總高為 $h$。
在 $\triangle AOB$ 中，
$C$ 是 $AO$ 的中點，且 $CD\ \parallel\ OB$
因此，
$\frac{\mathrm{OB}}{\mathrm{CD}}=\frac{\mathrm{AO}}{\mathrm{AC}}$
$\Rightarrow \frac{10}{\mathrm{CD}}=\frac{h}{\frac{h}{2}}$
$\Rightarrow \frac{10}{\mathrm{CD}}=\frac{2}{1}$
$\Rightarrow \mathrm{CD}=\frac{10}{2}=5 \mathrm{~cm}$
這意味著，
$r_{2}=5 \mathrm{~cm}$
小圓錐的體積 $=\frac{1}{3} \pi r_{2}^{2} \frac{h}{2}$
$=\frac{1}{3} \pi \times 5^2 \times \frac{h}{2}$
$=\frac{25}{6} \pi h$
臺體的體積 $=\frac{1}{3} \pi \frac{h}{2}(r_{1}^{2}+r_{1} r_{2}+r_{2}^{2})$
$=\frac{h \pi}{6}(10^{2}+10 \times 5+5^{2})$
$=\frac{\pi h}{6}(100+50+25)$
$=\frac{175}{6} \pi h$
上部分和下部分體積的比值 $=\frac{25}{6} \pi h: \frac{175}{6} \pi h$
$= 1: 7$
圓錐兩部分體積的比值為 $1:7$。
62 次瀏覽
