資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律一艘船的甲板上有一人，距離水面 \( 10 \mathrm{~m} \)。他觀察到一座懸崖頂部的仰角為 \( 45^{\circ} \)，底部的俯角為 \( 30^{\circ} \)。計算懸崖到船的距離和懸崖的高度。
已知
一艘船的甲板上有一人，距離水面 \( 10 \mathrm{~m} \)。他觀察到一座懸崖頂部的仰角為 \( 45^{\circ} \)，底部的俯角為 \( 30^{\circ} \)。
要求
我們需要找到懸崖到船的距離和懸崖的高度。
解答
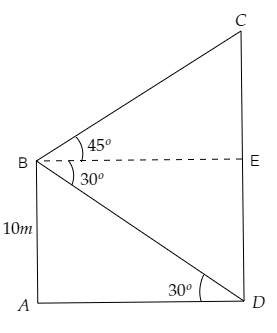
設 $CD$ 為懸崖，且人在船 $AB$ 的甲板上 $B$ 點。
從 $B$ 點觀察到懸崖 $CD$ 底部 $D$ 的俯角為 $30^{o}$，從 $B$ 點觀察到懸崖 $CD$ 頂部 $C$ 的仰角為 $45^{o}$。
設懸崖的高度為 $h\ m$。
從圖中，
$\angle ADB =30^{o}, AB=10\ m$ 且 $\angle CBE=45^{o}$
這意味著，
$ED=AB=10\ m$ 且 $CE=h-10\ m$
在 $\vartriangle CBE$ 中，
$tan 45^{o} =\frac{CE}{BE} =\frac{h-10}{x}$
$1 =\frac{h-10}{x}$
$x=h-10$.........(i)
在 $\vartriangle ABD$ 中，
$tan 30^{o}=\frac{AB}{AD} =\frac{10}{x}$
$\frac{1}{\sqrt{3}} =\frac{10}{x}$
$x=10\sqrt{3}\ m$
將 $x=10\sqrt{3}$ 代入公式 (i)，得到，
$10\sqrt{3}=h-10$
$h=10+10\sqrt{3}\ m$
$h=10(1.732+1)\ m$
$h=10(2.732) = 27.32\ m$
$\Rightarrow x=27.32-10=17.32\ m$
因此，懸崖到船的距離為 $17.32 \ m$，懸崖的高度為 $27.32\ m$。
更新於: 2022年10月10日
203 次瀏覽
廣告