
無監督神經網路
顧名思義,這種型別的學習是在沒有老師監督的情況下進行的。這個學習過程是獨立的。在無監督學習下訓練ANN期間,將相似型別的輸入向量組合起來形成簇。當應用新的輸入模式時,神經網路會給出指示輸入模式所屬類別的輸出響應。在這種情況下,不會有來自環境的反饋來告知期望的輸出是什麼以及它是否正確。因此,在這種型別的學習中,網路本身必須從輸入資料中發現模式、特徵以及輸入資料與輸出之間的關係。
贏家通吃網路
這類網路基於競爭學習規則,並將使用一種策略,即選擇具有最大總輸入的神經元作為贏家。輸出神經元之間的連線顯示了它們之間的競爭,其中一個將為“開”,這意味著它將是贏家,而其他將為“關”。
以下是基於此簡單概念使用無監督學習的一些網路。
漢明網路
在大多數使用無監督學習的神經網路中,計算距離和進行比較是必不可少的。這種網路是漢明網路,對於每個給定的輸入向量,它將被聚類到不同的組中。以下是漢明網路的一些重要特徵:
Lippmann於1987年開始研究漢明網路。
它是一個單層網路。
輸入可以是二進位制{0, 1}或雙極性{-1, 1}。
網路的權重由示例向量計算。
它是一個固定權重網路,這意味著即使在訓練期間權重也會保持不變。
Max網路
這也是一個固定權重網路,用作選擇具有最高輸入的節點的子網。所有節點都是完全互連的,並且在所有這些加權互連中都存在對稱權重。
架構
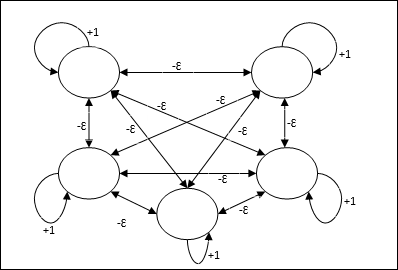
它使用迭代過程的機制,每個節點都透過連線從所有其他節點接收抑制性輸入。值最大的單個節點將處於活動狀態或獲勝狀態,而所有其他節點的啟用都將處於非活動狀態。Max網路使用恆等啟用函式,其公式為:$$f(x)\:=\:\begin{cases}x & if\:x > 0\\0 & if\:x \leq 0\end{cases}$$
該網路的任務透過+1的自激權重和互抑制幅度來完成,該幅度設定為[0 < ɛ < $\frac{1}{m}$],其中“m”是節點的總數。
ANN中的競爭學習
它關注無監督訓練,其中輸出節點試圖相互競爭以表示輸入模式。要理解這個學習規則,我們將不得不理解如下解釋的競爭網路:
競爭網路的基本概念
這個網路就像一個單層前饋網路,在輸出之間具有反饋連線。輸出之間的連線是抑制型別的,用虛線表示,這意味著競爭者永遠不會支援自己。
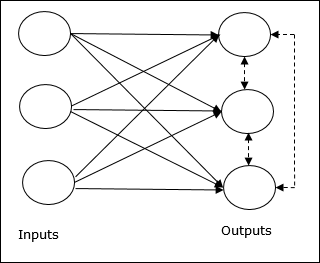
競爭學習規則的基本概念
如前所述,輸出節點之間會存在競爭,因此主要概念是:在訓練期間,對給定輸入模式具有最高啟用的輸出單元將被宣佈為贏家。此規則也稱為贏家通吃,因為只有獲勝神經元會更新,其餘神經元保持不變。
數學公式
以下是此學習規則數學公式的三個重要因素:
成為贏家的條件
假設如果神經元yk想要獲勝,則會有以下條件:
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k} > v_{j}\:for\:all\:\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
這意味著如果任何神經元(例如,yk)想要獲勝,則其誘導區域性場(求和單元的輸出),例如vk,必須是網路中所有其他神經元中最大的。
權重總和的條件
對競爭學習規則的另一個約束是,對特定輸出神經元的權重總和將為1。例如,如果我們考慮神經元k,則:
$$\displaystyle\sum\limits_{k} w_{kj}\:=\:1\:\:\:\:for\:all\:\:k$$
贏家的權重變化
如果神經元對輸入模式沒有響應,則該神經元不會發生學習。但是,如果特定神經元獲勝,則相應權重將如下調整:
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0 & if\:neuron\:k\:losses\end{cases}$$
這裡$\alpha$是學習率。
這清楚地表明我們透過調整其權重來偏袒獲勝神經元,如果神經元輸了,則我們無需費心重新調整其權重。
K均值聚類演算法
K均值是最流行的聚類演算法之一,其中我們使用分割槽過程的概念。我們從初始分割槽開始,反覆將模式從一個聚類移動到另一個聚類,直到得到令人滿意的結果。
演算法
步驟1 - 選擇k個點作為初始質心。初始化k個原型(w1,…,wk),例如,我們可以透過隨機選擇的輸入向量來識別它們:
$$W_{j}\:=\:i_{p},\:\:\: where\:j\:\in \lbrace1,....,k\rbrace\:and\:p\:\in \lbrace1,....,n\rbrace$$
每個聚類Cj都與原型wj相關聯。
步驟2 - 重複步驟3-5,直到E不再減小,或聚類成員資格不再改變。
步驟3 - 對於每個輸入向量ip,其中p ∈ {1,…,n},將ip放入具有最近原型的聚類Cj*中,該原型具有以下關係:
$$|i_{p}\:-\:w_{j*}|\:\leq\:|i_{p}\:-\:w_{j}|,\:j\:\in \lbrace1,....,k\rbrace$$
步驟4 - 對於每個聚類Cj,其中j ∈ { 1,…,k},更新原型wj為當前在Cj中的所有樣本的質心,以便:
$$w_{j}\:=\:\sum_{i_{p}\in C_{j}}\frac{i_{p}}{|C_{j}|}$$
步驟5 - 計算總量化誤差如下:
$$E\:=\:\sum_{j=1}^k\sum_{i_{p}\in w_{j}}|i_{p}\:-\:w_{j}|^2$$
神經認知機
它是一個多層前饋網路,由Fukushima在20世紀80年代開發。該模型基於監督學習,用於視覺模式識別,主要是手寫字元。它基本上是Cognitron網路的擴充套件,Cognitron網路也是由Fukushima在1975年開發的。
架構
它是一個分層網路,包含許多層,並且在這些層中存在區域性連線模式。
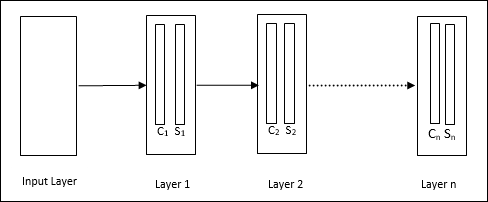
正如我們在上圖中看到的,神經認知機被劃分為不同的連線層,每一層都有兩個單元。這些單元的解釋如下:
S單元 - 它被稱為簡單單元,經過訓練可以響應特定模式或一組模式。
C單元 - 它被稱為複雜單元,它組合來自S單元的輸出,同時減少每個陣列中的單元數量。換句話說,C單元會置換S單元的結果。
訓練演算法
神經認知機的訓練被發現是逐層進行的。從輸入層到第一層的權重被訓練並凍結。然後,訓練從第一層到第二層的權重,依此類推。S單元和C單元之間的內部計算取決於來自先前層的權重。因此,我們可以說訓練演算法取決於S單元和C單元的計算。
S單元中的計算
S單元擁有從前一層接收的興奮性訊號,並擁有在同一層內獲得的抑制性訊號。
$$\theta=\:\sqrt{\sum\sum t_{i} c_{i}^2}$$
這裡,ti是固定權重,ci是來自C單元的輸出。
S單元的縮放輸入可以計算如下:
$$x\:=\:\frac{1\:+\:e}{1\:+\:vw_{0}}\:-\:1$$
這裡,$e\:=\:\sum_i c_{i}w_{i}$
wi是從C單元到S單元的可調權重。
w0是輸入和S單元之間可調的權重。
v是來自C單元的興奮性輸入。
輸出訊號的啟用為:
$$s\:=\:\begin{cases}x, & if\:x \geq 0\\0, & if\:x < 0\end{cases}$$
C單元中的計算
C層的淨輸入為:
$$C\:=\:\displaystyle\sum\limits_i s_{i}x_{i}$$
這裡,si是來自S單元的輸出,xi是從S單元到C單元的固定權重。
最終輸出如下:
$$C_{out}\:=\:\begin{cases}\frac{C}{a+C}, & if\:C > 0\\0, & otherwise\end{cases}$$
這裡“a”是取決於網路效能的引數。