
人工神經網路 - 學習與適應
如前所述,ANN完全受到生物神經系統,即人腦工作方式的啟發。人腦最令人印象深刻的特點是學習,因此ANN也獲得了同樣的特性。
什麼是ANN中的學習?
基本上,學習意味著根據環境的變化而進行自身調整和適應。ANN是一個複雜系統,更準確地說,它是一個複雜的自適應系統,它可以根據透過它的資訊改變其內部結構。
為什麼學習很重要?
作為一個複雜的自適應系統,ANN中的學習意味著處理單元能夠由於環境的變化而改變其輸入/輸出行為。由於構建特定網路時啟用函式和輸入/輸出向量是固定的,因此ANN中學習的重要性就提高了。現在要改變輸入/輸出行為,我們需要調整權重。
分類
它可以定義為透過查詢相同類別樣本之間的共同特徵來學習將樣本資料區分到不同類別中的過程。例如,為了執行ANN的訓練,我們有一些具有獨特特徵的訓練樣本,為了執行其測試,我們有一些具有其他獨特特徵的測試樣本。分類是監督學習的一個例子。
神經網路學習規則
我們知道,在ANN學習過程中,要改變輸入/輸出行為,我們需要調整權重。因此,需要一種可以修改權重的方法。這些方法稱為學習規則,它們只是演算法或方程。以下是神經網路的一些學習規則:
Hebb學習規則
這條規則是最古老和最簡單的規則之一,由唐納德·赫布 (Donald Hebb) 在他1949年的著作《行為的組織》(The Organization of Behavior) 中提出。它是一種前饋無監督學習。
基本概念 - 這條規則基於赫布提出的一個假設,他寫道:
“當細胞A的軸突足夠接近於激發細胞B,並且反覆或持續地參與激發它時,在一個或兩個細胞中都會發生某種生長過程或代謝變化,從而提高了A作為激發B的細胞之一的效率。”
從上述假設中,我們可以得出結論,如果兩個神經元同時放電,則它們之間的連線可能會增強;如果它們在不同時間放電,則可能會減弱。
數學公式 - 根據Hebb學習規則,以下是每次步長增加連線權重的公式。
$$ \Delta w_{ji}(t) = \alpha x_{i}(t) \cdot y_{j}(t) $$
這裡,$ \Delta w_{ji}(t) $ = 在時間步長t時連線權重增加的增量
$ \alpha $ = 正的常數學習率
$ x_{i}(t) $ = 在時間步長t時來自突觸前神經元的輸入值
$ y_{i}(t) $ = 在相同時間步長t時突觸前神經元的輸出
感知器學習規則
這條規則是由羅森布拉特 (Rosenblatt) 提出的單層前饋網路的誤差校正監督學習演算法,具有線性啟用函式。
基本概念 - 由於其監督性質,為了計算誤差,需要將期望/目標輸出與實際輸出進行比較。如果發現有任何差異,則必須對連線權重進行更改。
數學公式 - 為了解釋其數學公式,假設我們有“n”個有限的輸入向量x(n),以及其期望/目標輸出向量t(n),其中n = 1到N。
現在可以計算輸出'y',如前面根據淨輸入所解釋的那樣,並應用於該淨輸入的啟用函式可以表示如下:
$$ y = f(y_{in}) = \begin{cases} 1, & y_{in} > \theta \\ 0, & y_{in} \le \theta \end{cases} $$
其中θ是閾值。
權重的更新可以在以下兩種情況下進行:
情況一 - 當t ≠ y時,則
$$ w(new) = w(old) + tx $$
情況二 - 當t = y時,則
權重不變
Delta學習規則 (Widrow-Hoff規則)
它是由伯納德·維德羅 (Bernard Widrow) 和馬西恩·霍夫 (Marcian Hoff) 提出的,也稱為最小均方 (LMS) 方法,用於最小化所有訓練模式的誤差。它是一種具有連續啟用函式的監督學習演算法。
基本概念 - 這條規則的基礎是梯度下降法,它會無限持續下去。Delta規則更新突觸權重,以最小化輸出單元的淨輸入和目標值之間的差異。
數學公式 - 為了更新突觸權重,Delta規則由下式給出
$$ \Delta w_{i} = \alpha \cdot x_{i} \cdot e_{j} $$
這裡 $ \Delta w_{i} $ = 第i個模式的權重變化;
$ \alpha $ = 正的常數學習率;
$ x_{i} $ = 來自突觸前神經元的輸入值;
$ e_{j} $ = $ (t - y_{in}) $,期望/目標輸出與實際輸出 $ y_{in} $ 之間的差值
上述Delta規則僅適用於單個輸出單元。
權重的更新可以在以下兩種情況下進行:
情況一 - 當t ≠ y時,則
$$ w(new) = w(old) + \Delta w $$
情況二 - 當t = y時,則
權重不變
競爭學習規則 (贏者通吃)
它關注的是無監督訓練,其中輸出節點相互競爭以表示輸入模式。要理解這個學習規則,我們必須理解如下所示的競爭網路:
競爭網路的基本概念 - 這個網路就像一個單層前饋網路,輸出之間有反饋連線。輸出之間的連線是抑制型別的,用虛線表示,這意味著競爭者永遠不會相互支援。
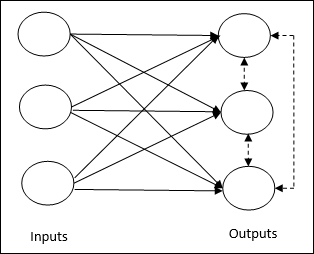
競爭學習規則的基本概念 - 如前所述,輸出節點之間會存在競爭。因此,主要概念是,在訓練過程中,對給定輸入模式具有最高啟用的輸出單元將被宣佈為獲勝者。這條規則也稱為贏者通吃,因為只有獲勝神經元會更新,其餘神經元保持不變。
數學公式 - 以下是該學習規則數學公式的三個重要因素:
獲勝條件 - 如果神經元 $ y_{k} $ 想獲勝,則會有以下條件:
$$ y_{k} = \begin{cases} 1 & \text{if } v_{k} > v_{j} \text{ for all } j, j \ne k \\ 0 & \text{otherwise} \end{cases} $$
這意味著如果任何神經元,例如 $ y_{k} $,想要獲勝,則其感應區域性場(求和單元的輸出),例如 $ v_{k} $,必須是網路中所有其他神經元中最大的。
權重總和條件 - 競爭學習規則的另一個約束是,特定輸出神經元的權重總和將為1。例如,如果我們考慮神經元k,則:
$$ \sum_{j} w_{kj} = 1 \quad \text{for all } k $$
獲勝者的權重變化 - 如果神經元對輸入模式沒有響應,則該神經元不會發生學習。但是,如果特定神經元獲勝,則相應權重將調整如下:
$$ \Delta w_{kj} = \begin{cases} -\alpha(x_{j} - w_{kj}), & \text{if neuron } k \text{ wins} \\ 0, & \text{if neuron } k \text{ loses} \end{cases} $$
這裡 $ \alpha $ 是學習率。
這清楚地表明,我們透過調整其權重來偏向獲勝神經元,如果存在神經元損失,則我們不必費心重新調整其權重。
Outstar學習規則
這條規則由格羅斯伯格 (Grossberg) 提出,它關注的是監督學習,因為期望輸出是已知的。它也稱為格羅斯伯格學習。
基本概念 - 這條規則應用於排列在一層中的神經元。它專門設計用於產生p個神經元層的期望輸出d。
數學公式 - 此規則中的權重調整計算如下:
$$ \Delta w_{j} = \alpha (d - w_{j}) $$
這裡d是期望神經元輸出,$ \alpha $ 是學習率。