
人工神經網路 - 基本概念
神經網路是平行計算裝置,它本質上是試圖建立大腦的計算機模型。其主要目標是開發一個系統,使其能夠比傳統系統更快地執行各種計算任務。這些任務包括模式識別和分類、逼近、最佳化和資料聚類。
什麼是人工神經網路?
人工神經網路(ANN)是一種高效的計算系統,其核心主題借鑑了生物神經網路的類比。ANN也被稱為“人工神經系統”、“並行分散式處理系統”或“連線主義系統”。ANN 獲取大量相互連線的單元,這些單元以某種模式連線以允許單元之間進行通訊。這些單元,也稱為節點或神經元,是並行執行的簡單處理器。
每個神經元都透過連線鏈路與其他神經元連線。每個連線鏈路都與一個權重相關聯,該權重包含有關輸入訊號的資訊。這是神經元解決特定問題最有用的資訊,因為權重通常會激發或抑制正在傳遞的訊號。每個神經元都有一個內部狀態,稱為啟用訊號。輸出訊號是在組合輸入訊號和啟用規則後產生的,可以傳送到其他單元。
ANN 的簡史
ANN 的歷史可以分為以下三個時期:
1940 年代至 1960 年代的 ANN
這個時期的幾個關鍵發展如下:
1943 - 人們認為,神經網路的概念始於生理學家沃倫·麥卡洛克和數學家沃爾特·皮茨的工作,他們在 1943 年使用電路對一個簡單的神經網路進行了建模,以描述大腦中的神經元如何工作。
1949 - 唐納德·赫布的著作《行為的組織》提出,一個神經元對另一個神經元的重複啟用會增加它們每次使用時的強度。
1956 - 泰勒引入了聯想記憶網路。
1958 - 羅森布拉特發明了一種用於麥卡洛克和皮茨神經元模型的學習方法,名為感知器。
1960 - 伯納德·維德羅和馬西安·霍夫開發了名為“ADALINE”和“MADALINE”的模型。
1960 年代至 1980 年代的 ANN
這個時期的幾個關鍵發展如下:
1961 - 羅森布拉特進行了一次不成功的嘗試,但提出了用於多層網路的“反向傳播”方案。
1964 - 泰勒構建了一個贏者通吃的電路,輸出單元之間存在抑制。
1969 - 明斯基和帕普特發明了多層感知器 (MLP)。
1971 - 科霍寧開發了聯想記憶。
1976 - 斯蒂芬·格羅斯伯格和蓋爾·卡彭特開發了自適應諧振理論。
1980 年代至今的 ANN
這個時期的幾個關鍵發展如下:
1982 - 主要發展是霍普菲爾德的能量方法。
1985 - 阿克利、欣頓和塞諾夫斯基開發了玻爾茲曼機。
1986 - 魯梅哈特、欣頓和威廉姆斯引入了廣義 delta 規則。
1988 - 科斯科開發了二元聯想記憶 (BAM),並提出了 ANN 中模糊邏輯的概念。
歷史回顧表明,該領域取得了顯著進展。基於神經網路的晶片正在出現,並正在開發針對複雜問題的應用。毫無疑問,今天是神經網路技術的一個過渡時期。
生物神經元
神經細胞(神經元)是一種特殊的生物細胞,負責處理資訊。據估計,神經元的數量巨大,大約為 1011 個,並且具有大量相互連線,大約為 1015 個。
示意圖
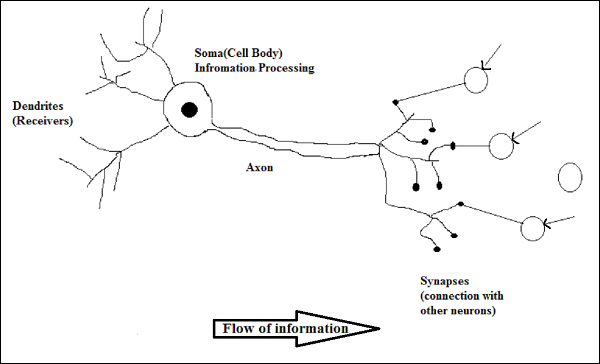
生物神經元的工作原理
如上圖所示,一個典型的神經元由以下四個部分組成,我們可以用它們來解釋其工作原理:
樹突 - 它們是樹狀分支,負責接收與其連線的其他神經元的資訊。換句話說,我們可以說它們像神經元的耳朵。
胞體 - 它是神經元的細胞體,負責處理從樹突接收到的資訊。
軸突 - 它就像一條電纜,神經元透過它傳送資訊。
突觸 - 它是軸突和其他神經元樹突之間的連線。
ANN 與 BNN
在檢視人工神經網路 (ANN) 和生物神經網路 (BNN) 之間的區別之前,讓我們先看看這兩個術語之間的相似之處。
| 生物神經網路 (BNN) | 人工神經網路 (ANN) |
|---|---|
| 胞體 | 節點 |
| 樹突 | 輸入 |
| 突觸 | 權重或互連 |
| 軸突 | 輸出 |
下表顯示了基於某些提到的標準對 ANN 和 BNN 的比較。
| 標準 | BNN | ANN |
|---|---|---|
| 處理 | 大規模並行,速度慢但優於 ANN | 大規模並行,速度快但劣於 BNN |
| 大小 | 1011 個神經元和 1015 個互連 | 102 到 104 個節點(主要取決於應用程式型別和網路設計者) |
| 學習 | 它們可以容忍模糊性 | 需要非常精確、結構化和格式化的資料才能容忍模糊性 |
| 容錯性 | 即使部分損壞,效能也會下降 | 它能夠提供強大的效能,因此具有容錯的潛力 |
| 儲存容量 | 將資訊儲存在突觸中 | 將資訊儲存在連續的記憶體位置中 |
人工神經網路模型
下圖表示 ANN 的通用模型及其處理過程。
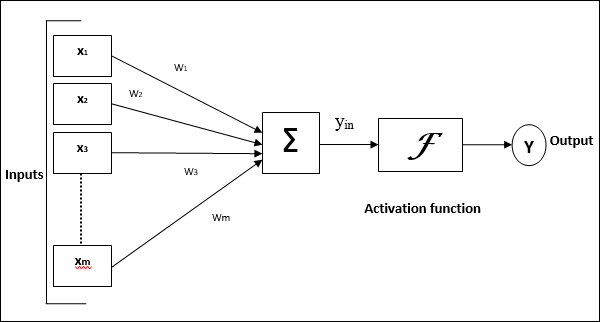
對於上述人工神經網路的通用模型,淨輸入可以計算如下:
$$y_{in}\:=\:x_{1}.w_{1}\:+\:x_{2}.w_{2}\:+\:x_{3}.w_{3}\:\dotso\: x_{m}.w_{m}$$
即,淨輸入 $y_{in}\:=\:\sum_i^m\:x_{i}.w_{i}$
可以透過對淨輸入應用啟用函式來計算輸出。
$$Y\:=\:F(y_{in}) $$
輸出 = 函式(計算的淨輸入)