
人工神經網路 - 快速指南
人工神經網路 - 基本概念
神經網路是平行計算裝置,它基本上是嘗試建立大腦的計算機模型。其主要目標是開發一個比傳統系統更快地執行各種計算任務的系統。這些任務包括模式識別和分類、逼近、最佳化和資料聚類。
什麼是人工神經網路?
人工神經網路 (ANN) 是一種高效的計算系統,其核心主題借鑑了生物神經網路的類比。ANN 也被稱為“人工神經系統”、“並行分散式處理系統”或“連線主義系統”。ANN 獲取大量相互連線的單元,以某種模式允許單元之間進行通訊。這些單元,也稱為節點或神經元,是並行工作的簡單處理器。
每個神經元都透過連線鏈路與其他神經元連線。每個連線鏈路都與一個權重相關聯,該權重包含有關輸入訊號的資訊。這是神經元解決特定問題最有用的資訊,因為權重通常會激發或抑制正在傳遞的訊號。每個神經元都有一個內部狀態,稱為啟用訊號。輸出訊號是在組合輸入訊號和啟用規則後產生的,可以傳送到其他單元。
ANN 的簡史
ANN 的歷史可以分為以下三個時期:
1940 年代至 1960 年代的 ANN
這個時期的幾個關鍵發展如下:
1943 - 人們認為,神經網路的概念始於生理學家沃倫·麥卡洛克和數學家沃爾特·皮茨的工作,他們在 1943 年使用電路對簡單的神經網路建模,以描述大腦中的神經元如何工作。
1949 - 唐納德·赫布的著作《行為組織》闡述了一個事實,即一個神經元對另一個神經元的重複啟用會增加它們每次使用時的強度。
1956 - 泰勒介紹了一種聯想記憶網路。
1958 - 羅森布拉特發明了一種名為感知器的麥卡洛克-皮茨神經元模型的學習方法。
1960 - 伯納德·維德羅和馬西恩·霍夫開發了名為“ADALINE”和“MADALINE”的模型。
1960 年代至 1980 年代的 ANN
這個時期的幾個關鍵發展如下:
1961 - 羅森布拉特進行了一次不成功的嘗試,但提出了用於多層網路的“反向傳播”方案。
1964 - 泰勒構建了一個在輸出單元之間具有抑制的贏者通吃電路。
1969 - 明斯基和佩珀特發明了多層感知器 (MLP)。
1971 - 科霍寧開發了聯想記憶。
1976 - 斯蒂芬·格羅斯伯格和蓋爾·卡彭特開發了自適應諧振理論。
1980 年代至今的 ANN
這個時期的幾個關鍵發展如下:
1982 - 最重要的發展是霍普菲爾德的能量方法。
1985 - 阿克利、欣頓和塞喬諾夫斯基開發了玻爾茲曼機。
1986 - 魯梅爾哈特、欣頓和威廉姆斯引入了廣義 delta 規則。
1988 - 科斯科開發了二元聯想記憶 (BAM),並提出了 ANN 中的模糊邏輯概念。
歷史回顧表明,該領域取得了重大進展。基於神經網路的晶片正在出現,並且正在開發對複雜問題的應用。毫無疑問,今天是神經網路技術的一個轉型時期。
生物神經元
神經細胞(神經元)是一種特殊的生物細胞,它處理資訊。據估計,神經元的數量巨大,大約為 1011,並且具有大量互連,大約為 1015。
示意圖
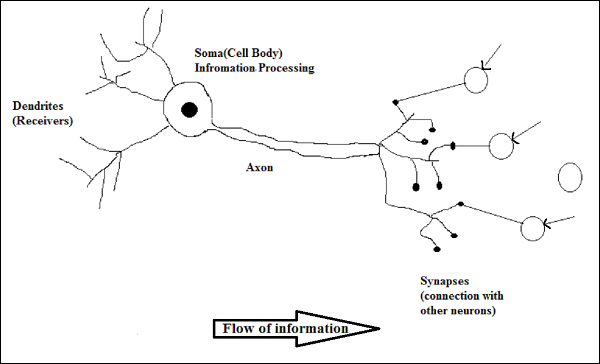
生物神經元的工作原理
如上圖所示,一個典型的神經元由以下四個部分組成,我們可以用它們來解釋其工作原理:
樹突 - 它們是樹狀分支,負責接收來自與其連線的其他神經元的資訊。換句話說,我們可以說它們像神經元的耳朵。
胞體 - 它是神經元的細胞體,負責處理從樹突接收到的資訊。
軸突 - 它就像一根電纜,神經元透過它傳送資訊。
突觸 - 它是軸突和其他神經元樹突之間的連線。
ANN 與 BNN
在檢視人工神經網路 (ANN) 和生物神經網路 (BNN) 之間的區別之前,讓我們先看看這兩者之間基於術語的相似之處。
| 生物神經網路 (BNN) | 人工神經網路 (ANN) |
|---|---|
| 胞體 | 節點 |
| 樹突 | 輸入 |
| 突觸 | 權重或互連 |
| 軸突 | 輸出 |
下表顯示了基於一些提到的標準對 ANN 和 BNN 的比較。
| 標準 | BNN | ANN |
|---|---|---|
| 處理 | 大規模並行,速度慢但優於 ANN | 大規模並行,速度快但劣於 BNN |
| 大小 | 1011 個神經元和 1015 個互連 | 102 到 104 個節點(主要取決於應用程式型別和網路設計者) |
| 學習 | 它們可以容忍模糊性 | 需要非常精確、結構化和格式化的資料才能容忍模糊性 |
| 容錯性 | 即使部分損壞,效能也會下降 | 它能夠實現強大的效能,因此具有容錯的潛力 |
| 儲存容量 | 將資訊儲存在突觸中 | 將資訊儲存在連續的記憶體位置中 |
人工神經網路模型
下圖表示 ANN 的通用模型及其處理過程。
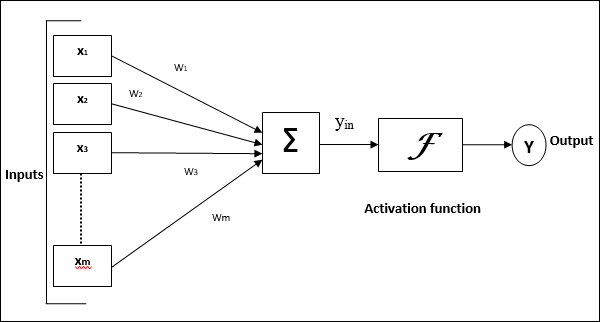
對於上述人工神經網路的通用模型,淨輸入的計算方法如下:
$$y_{in}\:=\:x_{1}.w_{1}\:+\:x_{2}.w_{2}\:+\:x_{3}.w_{3}\:\dotso\: x_{m}.w_{m}$$
即,淨輸入 $y_{in}\:=\:\sum_i^m\:x_{i}.w_{i}$
可以透過對淨輸入應用啟用函式來計算輸出。
$$Y\:=\:F(y_{in}) $$
輸出 = 函式(計算的淨輸入)
人工神經網路 - 構建模組
ANN 的處理取決於以下三個構建模組:
- 網路拓撲
- 權重調整或學習
- 啟用函式
本章將詳細討論 ANN 的這三個構建模組
網路拓撲
網路拓撲是網路及其節點和連線線的排列。根據拓撲結構,ANN 可以分為以下幾種:
前饋網路
它是一個非迴圈網路,其處理單元/節點分層排列,並且一層中的所有節點都與前一層的節點連線。連線具有不同的權重。沒有反饋環路,這意味著訊號只能沿一個方向流動,從輸入到輸出。它可以分為以下兩種型別:
單層前饋網路 - 是指只有一個加權層的反饋式 ANN。換句話說,我們可以說輸入層與輸出層完全連線。
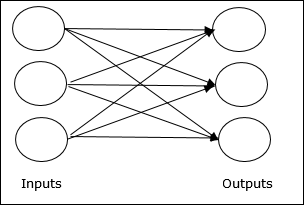
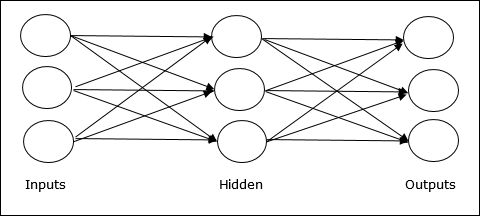
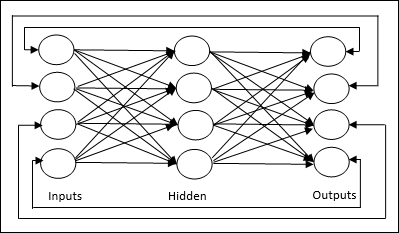
多層前饋網路 - 是指具有多個加權層的反饋式 ANN。由於該網路在輸入層和輸出層之間有一個或多個層,因此稱為隱藏層。
反饋網路
顧名思義,反饋網路具有反饋路徑,這意味著訊號可以使用迴圈沿兩個方向流動。這使其成為一個非線性動態系統,它會不斷變化,直到達到平衡狀態。它可以分為以下幾種型別:
迴圈網路 - 它們是具有閉環的反饋網路。以下是兩種型別的迴圈網路。
完全迴圈網路 - 它是最簡單的神經網路架構,因為所有節點都連線到所有其他節點,並且每個節點都充當輸入和輸出。
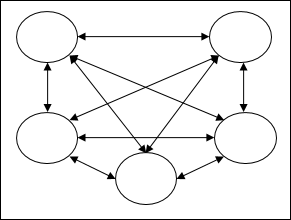
Jordan 網路 - 它是一個閉環網路,其中輸出將作為反饋再次進入輸入,如下面的圖所示。
權重調整或學習
在人工神經網路中,學習是修改指定網路神經元之間連線權重的方法。ANN 中的學習可以分為三類,即監督學習、無監督學習和強化學習。
監督學習
顧名思義,這種型別的學習是在教師的監督下進行的。這個學習過程是依賴性的。
在監督學習下訓練 ANN 期間,將輸入向量呈現給網路,這將產生輸出向量。該輸出向量與所需輸出向量進行比較。如果實際輸出與所需輸出向量之間存在差異,則會生成誤差訊號。根據此誤差訊號,調整權重,直到實際輸出與所需輸出匹配。
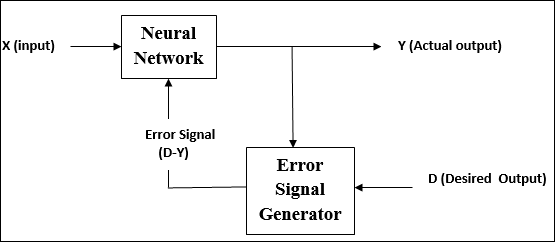
無監督學習
顧名思義,這種型別的學習是在沒有教師監督的情況下進行的。這個學習過程是獨立的。
在無監督學習下訓練 ANN 期間,將相似型別的輸入向量組合起來形成聚類。當應用新的輸入模式時,神經網路將給出指示輸入模式所屬類別的輸出響應。
沒有來自環境的關於所需輸出是什麼以及它是否正確的反饋。因此,在這種型別的學習中,網路本身必須從輸入資料中發現模式和特徵,以及輸入資料對輸出的關係。
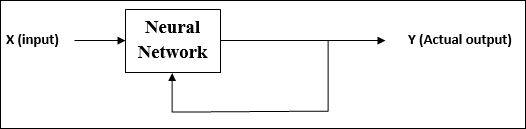
強化學習
顧名思義,這種型別的學習用於加強或強化網路的一些評論資訊。這個學習過程類似於監督學習,但是我們可能只有很少的資訊。
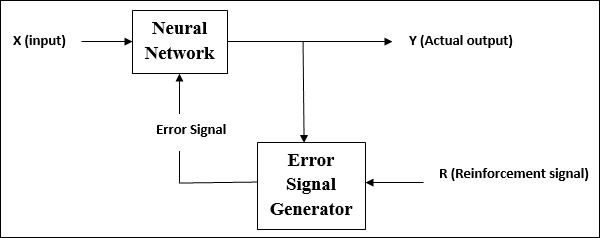
在強化學習下訓練網路期間,網路會從環境中接收一些反饋。這使其與監督學習有些相似。但是,此處獲得的反饋是評估性的,而不是指導性的,這意味著與監督學習中一樣,沒有教師。在收到反饋後,網路會調整權重以在將來獲得更好的評論資訊。
啟用函式
它可以定義為施加在輸入上的額外力量或努力以獲得精確的輸出。在 ANN 中,我們也可以對輸入應用啟用函式以獲得精確的輸出。以下是我們感興趣的一些啟用函式:
線性啟用函式
它也稱為恆等函式,因為它不執行任何輸入編輯。它可以定義為:
$$F(x)\:=\:x$$
S 型啟用函式
它有兩種型別,如下所示:
二元 S 型函式 - 此啟用函式將輸入編輯在 0 和 1 之間。它具有正性質。它始終是有界的,這意味著其輸出不能小於 0 且大於 1。它也是嚴格遞增的,這意味著輸入越多,輸出越高。它可以定義為
$$F(x)\:=\:sigm(x)\:=\:\frac{1}{1\:+\:exp(-x)}$$
雙極S型函式 − 此啟用函式將輸入編輯在-1和1之間。它可以是正數或負數。它始終是有界的,這意味著其輸出不能小於-1且大於1。它也像S型函式一樣嚴格遞增。它可以定義為
$$F(x)\:=\:sigm(x)\:=\:\frac{2}{1\:+\:exp(-x)}\:-\:1\:=\:\frac{1\:-\:exp(x)}{1\:+\:exp(x)}$$
學習和適應
如前所述,人工神經網路完全受到生物神經系統,即人腦工作方式的啟發。人腦最令人印象深刻的特點是學習,因此人工神經網路也獲得了同樣的特徵。
人工神經網路中的學習是什麼?
基本上,學習意味著根據環境的變化而進行自身改變和適應。人工神經網路是一個複雜的系統,更準確地說,它是一個複雜的適應性系統,它可以根據透過它的資訊改變其內部結構。
為什麼它很重要?
作為一個複雜的適應性系統,人工神經網路中的學習意味著處理單元能夠由於環境的變化而改變其輸入/輸出行為。由於構建特定網路時啟用函式以及輸入/輸出向量是固定的,因此人工神經網路中學習的重要性有所提高。現在要改變輸入/輸出行為,我們需要調整權重。
分類
它可以定義為透過查詢相同類別樣本之間的共同特徵來學習將樣本資料區分到不同類別中的過程。例如,為了執行人工神經網路的訓練,我們有一些具有獨特特徵的訓練樣本,為了執行其測試,我們有一些具有其他獨特特徵的測試樣本。分類是有監督學習的一個例子。
神經網路學習規則
我們知道,在人工神經網路學習過程中,要改變輸入/輸出行為,我們需要調整權重。因此,需要一種可以修改權重的方法。這些方法稱為學習規則,它們只是演算法或方程。以下是神經網路的一些學習規則:
Hebb學習規則
這條規則是最古老和最簡單的規則之一,由Donald Hebb在1949年的著作《行為的組織》中提出。它是一種前饋、無監督學習。
基本概念 − 這條規則基於Hebb提出的一個假設,他寫道:
“當細胞A的軸突足夠接近於激發細胞B,並反覆或持續地參與其激發時,一個或兩個細胞中會發生一些生長過程或代謝變化,從而提高A作為激發B的細胞之一的效率。”
從上述假設中,我們可以得出結論:如果兩個神經元同時激發,則它們之間的連線可能會加強;如果它們在不同時間激發,則連線可能會減弱。
數學公式 − 根據Hebb學習規則,以下是每次步長增加連線權重的公式。
$$\Delta w_{ji}(t)\:=\:\alpha x_{i}(t).y_{j}(t)$$
這裡,$\Delta w_{ji}(t)$ = 在時間步長t時連線權重增加的增量
$\alpha$ = 正的常數學習率
$x_{i}(t)$ = 在時間步長t時來自突觸前神經元的輸入值
$y_{i}(t)$ = 在相同時間步長t時突觸前神經元的輸出
感知器學習規則
這條規則是由Rosenblatt提出的單層前饋網路的線性啟用函式的誤差校正監督學習演算法。
基本概念 − 由於其監督性質,為了計算誤差,需要比較期望/目標輸出和實際輸出。如果發現有任何差異,則必須更改連線權重。
數學公式 − 為了解釋其數學公式,假設我們有'n'個有限輸入向量x(n),以及其期望/目標輸出向量t(n),其中n = 1到N。
現在可以計算輸出'y',如前面根據淨輸入解釋的那樣,並應用於該淨輸入的啟用函式可以表示為:
$$y\:=\:f(y_{in})\:=\:\begin{cases}1, & y_{in}\:>\:\theta \\0, & y_{in}\:\leqslant\:\theta\end{cases}$$
其中θ是閾值。
權重的更新可以在以下兩種情況下進行:
情況一 − 當t ≠ y時,則
$$w(new)\:=\:w(old)\:+\;tx$$
情況二 − 當t = y時,則
權重不變
Delta學習規則(Widrow-Hoff規則)
它是由Bernard Widrow和Marcian Hoff提出的,也稱為最小均方誤差(LMS)方法,用於最小化所有訓練模式的誤差。它是一種具有連續啟用函式的監督學習演算法。
基本概念 − 這條規則的基礎是梯度下降法,它會持續進行。Delta規則更新突觸權重,以最小化輸出單元的淨輸入和目標值之間的差異。
數學公式 − 為了更新突觸權重,Delta規則由下式給出
$$\Delta w_{i}\:=\:\alpha\:.x_{i}.e_{j}$$
這裡 $\Delta w_{i}$ = 第i個模式的權重變化;
$\alpha$ = 正的常數學習率;
$x_{i}$ = 來自突觸前神經元的輸入值;
$e_{j}$ = $(t\:-\:y_{in})$,期望/目標輸出與實際輸出$y_{in}$之間的差值
上述Delta規則僅適用於單個輸出單元。
權重的更新可以在以下兩種情況下進行:
情況一 − 當t ≠ y時,則
$$w(new)\:=\:w(old)\:+\:\Delta w$$
情況二 − 當t = y時,則
權重不變
競爭學習規則(勝者為王)
它關注的是無監督訓練,其中輸出節點試圖相互競爭以表示輸入模式。為了理解這個學習規則,我們必須理解如下所示的競爭網路:
競爭網路的基本概念 − 此網路類似於具有輸出之間反饋連線的單層前饋網路。輸出之間的連線是抑制型別的,用虛線表示,這意味著競爭者永遠不會互相支援。
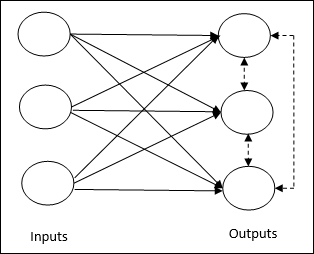
競爭學習規則的基本概念 − 如前所述,輸出節點之間會存在競爭。因此,主要的概念是,在訓練期間,對給定輸入模式具有最高啟用的輸出單元將被宣佈為獲勝者。該規則也稱為勝者為王,因為只有獲勝神經元被更新,其餘神經元保持不變。
數學公式 − 以下是此學習規則數學公式的三個重要因素:
獲勝條件 − 假設如果神經元$y_{k}$ 想要獲勝,則會有以下條件:
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k}\:>\:v_{j}\:for\:all\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
這意味著如果任何神經元,例如$y_{k}$ ,想要獲勝,則其誘導區域性場(求和單元的輸出),例如$v_{k}$,必須是網路中所有其他神經元中最大的。
權重總和條件 − 對競爭學習規則的另一個約束是,對特定輸出神經元的權重總和將為1。例如,如果我們考慮神經元k,則:
$$\displaystyle\sum\limits_{j}w_{kj}\:=\:1\:\:\:\:\:\:\:\:\:for\:all\:k$$
獲勝者的權重變化 − 如果神經元對輸入模式沒有響應,則該神經元不會發生學習。但是,如果特定神經元獲勝,則相應權重將按如下方式調整
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0, & if\:neuron\:k\:losses\end{cases}$$
這裡$\alpha$是學習率。
這清楚地表明,我們正在透過調整其權重來偏向獲勝神經元,如果存在神經元損失,則我們無需費心重新調整其權重。
Outstar學習規則
這條規則由Grossberg提出,它關注的是監督學習,因為期望輸出是已知的。它也稱為Grossberg學習。
基本概念 − 這條規則應用於按層排列的神經元。它專門設計用於產生p個神經元層的期望輸出d。
數學公式 − 此規則中的權重調整計算如下
$$\Delta w_{j}\:=\:\alpha\:(d\:-\:w_{j})$$
這裡d是期望神經元輸出,$\alpha$是學習率。
監督學習
顧名思義,監督學習是在教師的監督下進行的。此學習過程是依賴性的。在監督學習下訓練人工神經網路期間,輸入向量將被呈現給網路,這將產生一個輸出向量。此輸出向量將與期望/目標輸出向量進行比較。如果實際輸出與期望/目標輸出向量之間存在差異,則會生成誤差訊號。基於此誤差訊號,將調整權重,直到實際輸出與期望輸出匹配。
感知器
感知器由Frank Rosenblatt使用McCulloch和Pitts模型開發,是人工神經網路的基本操作單元。它採用監督學習規則,能夠將資料分類為兩類。
感知器的操作特性:它由具有任意數量輸入以及可調節權重的單個神經元組成,但神經元的輸出取決於閾值,為1或0。它還包括一個偏置,其權重始終為1。下圖給出了感知器的示意圖。
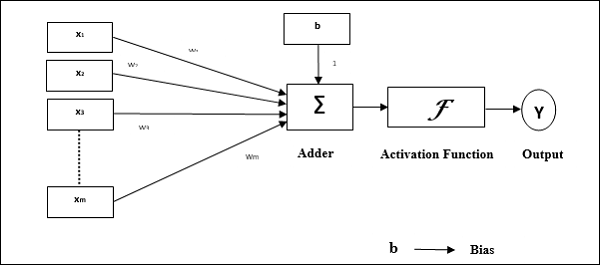
因此,感知器具有以下三個基本元素:
連線 − 它將有一組連線連結,這些連結攜帶權重,包括一個權重始終為1的偏置。
加法器 − 它在輸入與其各自權重相乘後對其進行加法。
啟用函式 − 它限制神經元的輸出。最基本的啟用函式是具有兩個可能輸出的Heaviside階躍函式。如果輸入為正,則此函式返回1;如果輸入為負,則返回0。
訓練演算法
感知器網路可以針對單個輸出單元以及多個輸出單元進行訓練。
單個輸出單元的訓練演算法
步驟1 − 初始化以下內容以開始訓練:
- 權重
- 偏置
- 學習率$\alpha$
為了簡化計算,權重和偏置必須設定為0,學習率必須設定為1。
步驟2 − 當停止條件不為真時,繼續步驟3-8。
步驟3 − 對於每個訓練向量x,繼續步驟4-6。
步驟 4 − 按如下方式啟用每個輸入單元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步驟 5 − 現在使用以下關係獲得淨輸入 −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}.\:w_{i}$$
這裡‘b’ 是偏置,‘n’ 是輸入神經元的總數。
步驟 6 − 應用以下啟用函式以獲得最終輸出。
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{in}\:\leqslant\:\theta\\-1 & if\:y_{in}\:<\:-\theta \end{cases}$$
步驟 7 − 按如下方式調整權重和偏置 −
情況 1 − 如果 y ≠ t,則
$$w_{i}(new)\:=\:w_{i}(old)\:+\:\alpha\:tx_{i}$$
$$b(new)\:=\:b(old)\:+\:\alpha t$$
情況 2 − 如果 y = t,則
$$w_{i}(new)\:=\:w_{i}(old)$$
$$b(new)\:=\:b(old)$$
這裡‘y’ 是實際輸出,‘t’ 是期望/目標輸出。
步驟 8 − 測試停止條件,當權重沒有變化時會發生。
多輸出單元的訓練演算法
下圖是用於多個輸出類的感知器架構。
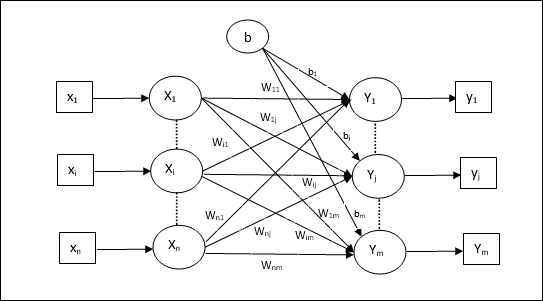
步驟1 − 初始化以下內容以開始訓練:
- 權重
- 偏置
- 學習率$\alpha$
為了簡化計算,權重和偏置必須設定為0,學習率必須設定為1。
步驟2 − 當停止條件不為真時,繼續步驟3-8。
步驟3 − 對於每個訓練向量x,繼續步驟4-6。
步驟 4 − 按如下方式啟用每個輸入單元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步驟 5 − 使用以下關係獲得淨輸入 −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}$$
這裡‘b’ 是偏置,‘n’ 是輸入神經元的總數。
步驟 6 − 應用以下啟用函式以獲得每個輸出單元j = 1 到 m的最終輸出 −
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{inj}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{inj}\:\leqslant\:\theta\\-1 & if\:y_{inj}\:<\:-\theta \end{cases}$$
步驟 7 − 如下調整x = 1 到 n和j = 1 到 m的權重和偏置 −
情況 1 − 如果 yj ≠ tj,則
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha\:t_{j}x_{i}$$
$$b_{j}(new)\:=\:b_{j}(old)\:+\:\alpha t_{j}$$
情況 2 − 如果 yj = tj,則
$$w_{ij}(new)\:=\:w_{ij}(old)$$
$$b_{j}(new)\:=\:b_{j}(old)$$
這裡‘y’ 是實際輸出,‘t’ 是期望/目標輸出。
步驟 8 − 測試停止條件,當權重沒有變化時會發生。
自適應線性神經元 (Adaline)
Adaline,即自適應線性神經元,是一個具有單個線性單元的網路。它由 Widrow 和 Hoff 於 1960 年開發。關於 Adaline 的一些要點如下 −
它使用雙極啟用函式。
它使用 delta 規則進行訓練,以最小化實際輸出與期望/目標輸出之間的均方誤差 (MSE)。
權重和偏置是可調整的。
架構
Adaline 的基本結構類似於感知器,它具有一個額外的反饋環路,藉助該環路,實際輸出與期望/目標輸出進行比較。根據訓練演算法進行比較後,將更新權重和偏置。
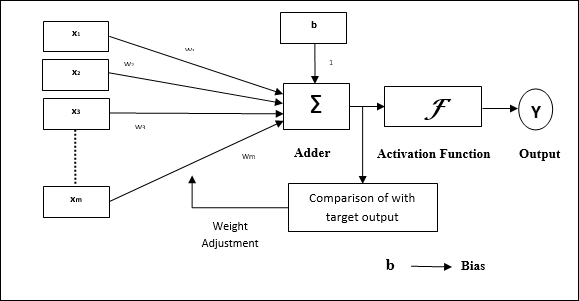
訓練演算法
步驟1 − 初始化以下內容以開始訓練:
- 權重
- 偏置
- 學習率$\alpha$
為了簡化計算,權重和偏置必須設定為0,學習率必須設定為1。
步驟2 − 當停止條件不為真時,繼續步驟3-8。
步驟 3 − 對每個雙極訓練對s:t繼續步驟 4-6。
步驟 4 − 按如下方式啟用每個輸入單元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步驟 5 − 使用以下關係獲得淨輸入 −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{i}$$
這裡‘b’ 是偏置,‘n’ 是輸入神經元的總數。
步驟 6 − 應用以下啟用函式以獲得最終輸出 −
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:\geqslant\:0 \\-1 & if\:y_{in}\:<\:0 \end{cases}$$
步驟 7 − 按如下方式調整權重和偏置 −
情況 1 − 如果 y ≠ t,則
$$w_{i}(new)\:=\:w_{i}(old)\:+\: \alpha(t\:-\:y_{in})x_{i}$$
$$b(new)\:=\:b(old)\:+\: \alpha(t\:-\:y_{in})$$
情況 2 − 如果 y = t,則
$$w_{i}(new)\:=\:w_{i}(old)$$
$$b(new)\:=\:b(old)$$
這裡‘y’ 是實際輸出,‘t’ 是期望/目標輸出。
$(t\:-\;y_{in})$ 是計算出的誤差。
步驟 8 − 測試停止條件,當權重沒有變化或訓練期間發生的最高權重變化小於指定的容差時會發生。
多自適應線性神經元 (Madaline)
Madaline,即多自適應線性神經元,是一個由許多 Adaline 並行組成的網路。它將具有單個輸出單元。關於 Madaline 的一些要點如下 −
它就像一個多層感知器,其中 Adaline 充當輸入層和 Madaline 層之間的隱藏單元。
輸入層和 Adaline 層之間的權重和偏置(如我們在 Adaline 架構中看到的)是可調整的。
Adaline 和 Madaline 層的權重和偏置固定為 1。
可以使用 Delta 規則進行訓練。
架構
Madaline 的架構由輸入層的“n”個神經元、Adaline 層的“m”個神經元和 Madaline 層的 1 個神經元組成。Adaline 層可以被認為是隱藏層,因為它位於輸入層和輸出層(即 Madaline 層)之間。
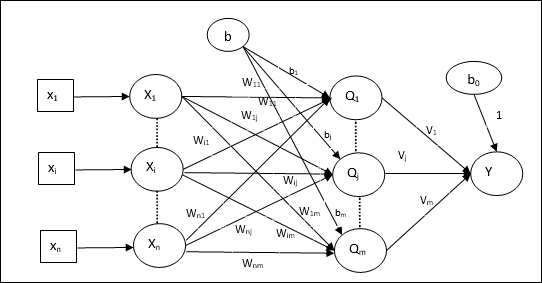
訓練演算法
到目前為止,我們知道只有輸入層和 Adaline 層之間的權重和偏置需要調整,而 Adaline 層和 Madaline 層之間的權重和偏置是固定的。
步驟1 − 初始化以下內容以開始訓練:
- 權重
- 偏置
- 學習率$\alpha$
為了簡化計算,權重和偏置必須設定為0,學習率必須設定為1。
步驟2 − 當停止條件不為真時,繼續步驟3-8。
步驟 3 − 對每個雙極訓練對s:t繼續步驟 4-7。
步驟 4 − 按如下方式啟用每個輸入單元 −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步驟 5 − 使用以下關係獲得每個隱藏層(即 Adaline 層)的淨輸入 −
$$Q_{inj}\:=\:b_{j}\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}\:\:\:j\:=\:1\:to\:m$$
這裡‘b’ 是偏置,‘n’ 是輸入神經元的總數。
步驟 6 − 應用以下啟用函式以獲得 Adaline 層和 Madaline 層的最終輸出 −
$$f(x)\:=\:\begin{cases}1 & if\:x\:\geqslant\:0 \\-1 & if\:x\:<\:0 \end{cases}$$
隱藏層 (Adaline) 單元的輸出
$$Q_{j}\:=\:f(Q_{inj})$$
網路的最終輸出
$$y\:=\:f(y_{in})$$
即 $\:\:y_{inj}\:=\:b_{0}\:+\:\sum_{j = 1}^m\:Q_{j}\:v_{j}$
步驟 7 − 計算誤差並如下調整權重 −
情況 1 − 如果 y ≠ t 且 t = 1,則
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\: \alpha(1\:-\:Q_{inj})x_{i}$$
$$b_{j}(new)\:=\:b_{j}(old)\:+\: \alpha(1\:-\:Q_{inj})$$
在這種情況下,將更新Qj上的權重,其中淨輸入接近 0,因為t = 1。
情況 2 − 如果 y ≠ t 且 t = -1,則
$$w_{ik}(new)\:=\:w_{ik}(old)\:+\: \alpha(-1\:-\:Q_{ink})x_{i}$$
$$b_{k}(new)\:=\:b_{k}(old)\:+\: \alpha(-1\:-\:Q_{ink})$$
在這種情況下,將更新Qk上的權重,其中淨輸入為正,因為t = -1。
這裡‘y’ 是實際輸出,‘t’ 是期望/目標輸出。
情況 3 − 如果 y = t,則
權重不會發生變化。
步驟 8 − 測試停止條件,當權重沒有變化或訓練期間發生的最高權重變化小於指定的容差時會發生。
反向傳播神經網路
反向傳播神經網路 (BPN) 是一個多層神經網路,由輸入層、至少一個隱藏層和輸出層組成。顧名思義,在這個網路中將進行反向傳播。透過比較目標輸出和實際輸出,在輸出層計算出的誤差將反向傳播到輸入層。
架構
如下圖所示,BPN 的架構具有三個相互連線的層,這些層上帶有權重。隱藏層和輸出層也具有偏置,其權重始終為 1。從圖中可以清楚地看出,BPN 的工作分為兩個階段。一個階段將訊號從輸入層傳送到輸出層,另一個階段將誤差從輸出層反向傳播到輸入層。
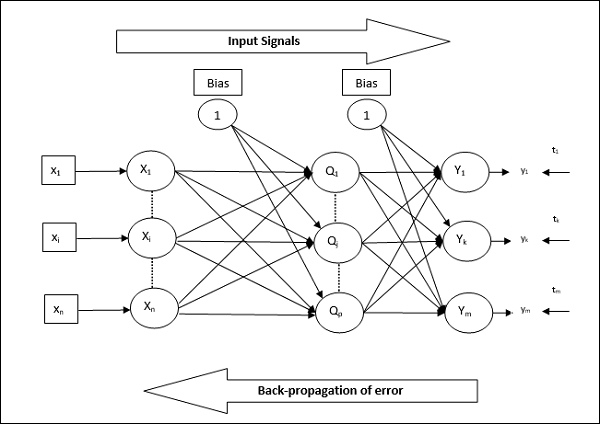
訓練演算法
對於訓練,BPN 將使用二進位制 sigmoid 啟用函式。BPN 的訓練將包含以下三個階段。
階段 1 − 前向傳播階段
階段 2 − 誤差反向傳播
階段 3 − 權重更新
所有這些步驟都將在以下演算法中總結
步驟1 − 初始化以下內容以開始訓練:
- 權重
- 學習率$\alpha$
為了簡化計算,請取一些小的隨機值。
步驟 2 − 當停止條件不成立時,繼續步驟 3-11。
步驟 3 − 對每一對訓練資料繼續步驟 4-10。
階段 1
步驟 4 − 每個輸入單元接收輸入訊號xi 並將其傳送到隱藏單元,所有i = 1 到 n
步驟 5 − 使用以下關係計算隱藏單元的淨輸入 −
$$Q_{inj}\:=\:b_{0j}\:+\:\sum_{i=1}^n x_{i}v_{ij}\:\:\:\:j\:=\:1\:to\:p$$
這裡b0j是隱藏單元上的偏置,vij是從輸入層的i單元到隱藏層的j單元的權重。
現在透過應用以下啟用函式計算淨輸出
$$Q_{j}\:=\:f(Q_{inj})$$
將這些隱藏層單元的輸出訊號傳送到輸出層單元。
步驟 6 − 使用以下關係計算輸出層單元的淨輸入 −
$$y_{ink}\:=\:b_{0k}\:+\:\sum_{j = 1}^p\:Q_{j}\:w_{jk}\:\:k\:=\:1\:to\:m$$
這裡b0k是輸出單元上的偏置,wjk是從隱藏層的j單元到輸出層的k單元的權重。
透過應用以下啟用函式計算淨輸出
$$y_{k}\:=\:f(y_{ink})$$
階段 2
步驟 7 − 計算每個輸出單元接收到的目標模式對應的誤差校正項,如下所示 −
$$\delta_{k}\:=\:(t_{k}\:-\:y_{k})f^{'}(y_{ink})$$
在此基礎上,更新權重和偏置,如下所示 −
$$\Delta v_{jk}\:=\:\alpha \delta_{k}\:Q_{ij}$$
$$\Delta b_{0k}\:=\:\alpha \delta_{k}$$
然後,將$\delta_{k}$反向傳播到隱藏層。
步驟 8 − 現在每個隱藏單元將是來自輸出單元的 delta 輸入的總和。
$$\delta_{inj}\:=\:\displaystyle\sum\limits_{k=1}^m \delta_{k}\:w_{jk}$$
誤差項可以計算如下 −
$$\delta_{j}\:=\:\delta_{inj}f^{'}(Q_{inj})$$
在此基礎上,更新權重和偏置,如下所示 −
$$\Delta w_{ij}\:=\:\alpha\delta_{j}x_{i}$$
$$\Delta b_{0j}\:=\:\alpha\delta_{j}$$
階段 3
步驟 9 − 每個輸出單元(ykk = 1 到 m)更新權重和偏置,如下所示 −
$$v_{jk}(new)\:=\:v_{jk}(old)\:+\:\Delta v_{jk}$$
$$b_{0k}(new)\:=\:b_{0k}(old)\:+\:\Delta b_{0k}$$
步驟 10 − 每個輸出單元(zjj = 1 到 p)更新權重和偏置,如下所示 −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\Delta w_{ij}$$
$$b_{0j}(new)\:=\:b_{0j}(old)\:+\:\Delta b_{0j}$$
步驟 11 − 檢查停止條件,這可能是達到時期數或目標輸出與實際輸出匹配。
廣義 Delta 學習規則
Delta 規則僅適用於輸出層。另一方面,廣義 Delta 規則(也稱為反向傳播規則)是建立隱藏層期望值的一種方法。
數學公式
對於啟用函式$y_{k}\:=\:f(y_{ink})$,隱藏層和輸出層上淨輸入的導數可以由下式給出
$$y_{ink}\:=\:\displaystyle\sum\limits_i\:z_{i}w_{jk}$$
並且$\:\:y_{inj}\:=\:\sum_i x_{i}v_{ij}$
現在必須最小化的誤差是
$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2$$
使用鏈式法則,我們有
$$\frac{\partial E}{\partial w_{jk}}\:=\:\frac{\partial }{\partial w_{jk}}(\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2)$$
$$=\:\frac{\partial }{\partial w_{jk}}\lgroup\frac{1}{2}[t_{k}\:-\:t(y_{ink})]^2\rgroup$$
$$=\:-[t_{k}\:-\:y_{k}]\frac{\partial }{\partial w_{jk}}f(y_{ink})$$
$$=\:-[t_{k}\:-\:y_{k}]f(y_{ink})\frac{\partial }{\partial w_{jk}}(y_{ink})$$
$$=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})z_{j}$$
現在讓我們說$\delta_{k}\:=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})$
連線到隱藏單元zj的權重可以由下式給出 −
$$\frac{\partial E}{\partial v_{ij}}\:=\:- \displaystyle\sum\limits_{k} \delta_{k}\frac{\partial }{\partial v_{ij}}\:(y_{ink})$$
代入$y_{ink}$的值,我們將得到以下結果
$$\delta_{j}\:=\:-\displaystyle\sum\limits_{k}\delta_{k}w_{jk}f^{'}(z_{inj})$$
權重更新可以如下進行 −
對於輸出單元 −
$$\Delta w_{jk}\:=\:-\alpha\frac{\partial E}{\partial w_{jk}}$$
$$=\:\alpha\:\delta_{k}\:z_{j}$$
對於隱藏單元 −
$$\Delta v_{ij}\:=\:-\alpha\frac{\partial E}{\partial v_{ij}}$$
$$=\:\alpha\:\delta_{j}\:x_{i}$$
無監督學習
顧名思義,這種型別的學習是在沒有教師監督的情況下進行的。這個學習過程是獨立的。在無監督學習下訓練 ANN 期間,將類似型別的輸入向量組合起來形成聚類。當應用新的輸入模式時,神經網路會給出指示輸入模式所屬類別的輸出響應。在這裡,不會有來自環境的反饋來指示期望輸出是什麼以及它是否正確。因此,在這種型別的學習中,網路本身必須從輸入資料中發現模式、特徵以及輸入資料與輸出之間的關係。
贏者通吃網路
這類網路基於競爭學習規則,並採用選擇總輸入量最大的神經元作為獲勝者的策略。輸出神經元之間的連線顯示了它們之間的競爭,其中一個神經元將處於“ON”狀態,這意味著它獲勝,而其他神經元將處於“OFF”狀態。
以下是基於此簡單概念使用無監督學習的一些網路。
Hamming 網路
在大多數使用無監督學習的神經網路中,計算距離和進行比較是必不可少的。這種網路是 Hamming 網路,對於每個給定的輸入向量,它將被聚類到不同的組中。以下是 Hamming 網路的一些重要特徵:
Lippmann 於 1987 年開始研究 Hamming 網路。
它是一個單層網路。
輸入可以是二進位制 {0, 1} 或雙極性 {-1, 1}。
網路的權重由示例向量計算。
它是一個固定權重網路,這意味著即使在訓練過程中權重也會保持不變。
Max 網路
這也是一個固定權重網路,用作選擇具有最高輸入的節點的子網。所有節點都完全互連,並且在所有這些加權互連中存在對稱權重。
架構
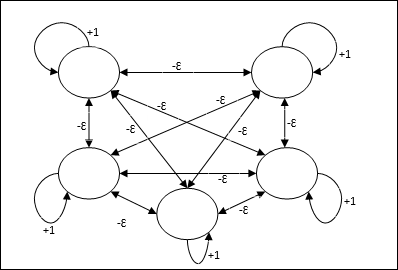
它使用迭代過程的機制,每個節點透過連線從所有其他節點接收抑制性輸入。值最大的單個節點將處於活動狀態或獲勝狀態,所有其他節點的啟用將處於非活動狀態。Max 網路使用恆等啟用函式,其公式為 $$f(x)\:=\:\begin{cases}x & if\:x > 0\\0 & if\:x \leq 0\end{cases}$$
該網路的任務是透過 +1 的自激權重和互抑制幅度來完成的,該幅度設定為 [0 < ɛ < $\frac{1}{m}$],其中“m”是節點的總數。
人工神經網路中的競爭學習
它關注無監督訓練,其中輸出節點相互競爭以表示輸入模式。為了理解這個學習規則,我們必須理解競爭網路,解釋如下:
競爭網路的基本概念
這個網路就像一個單層前饋網路,在輸出之間具有反饋連線。輸出之間的連線是抑制型別的,用虛線表示,這意味著競爭者永遠不會相互支援。
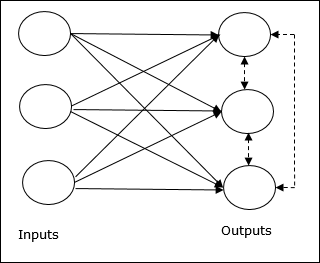
競爭學習規則的基本概念
如前所述,輸出節點之間會有競爭,因此主要概念是:在訓練期間,對給定輸入模式具有最高啟用的輸出單元將被宣佈為獲勝者。此規則也稱為贏者通吃,因為只有獲勝神經元會更新,其餘神經元保持不變。
數學公式
以下是此學習規則數學公式的三個重要因素:
獲勝條件
假設如果神經元yk想要獲勝,則會有以下條件:
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k} > v_{j}\:for\:all\:\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
這意味著如果任何神經元,例如yk想要獲勝,則其誘導區域性場(求和單元的輸出),例如vk,必須是網路中所有其他神經元中最大的。
權重總和條件
競爭學習規則的另一個約束是特定輸出神經元的權重總和將為 1。例如,如果我們考慮神經元k,則
$$\displaystyle\sum\limits_{k} w_{kj}\:=\:1\:\:\:\:for\:all\:\:k$$
獲勝者的權重變化
如果神經元對輸入模式沒有響應,則該神經元不會發生學習。但是,如果特定神經元獲勝,則相應權重將如下調整:
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0 & if\:neuron\:k\:losses\end{cases}$$
這裡$\alpha$是學習率。
這清楚地表明,我們透過調整其權重來偏向獲勝神經元,如果神經元失敗,則我們無需重新調整其權重。
K 均值聚類演算法
K 均值是最流行的聚類演算法之一,其中我們使用分割槽過程的概念。我們從初始分割槽開始,並反覆將模式從一個聚類移動到另一個聚類,直到我們得到令人滿意的結果。
演算法
步驟 1 - 選擇k個點作為初始質心。初始化k個原型(w1,…,wk),例如,我們可以透過隨機選擇的輸入向量來識別它們:
$$W_{j}\:=\:i_{p},\:\:\: where\:j\:\in \lbrace1,....,k\rbrace\:and\:p\:\in \lbrace1,....,n\rbrace$$
每個聚類Cj都與原型wj相關聯。
步驟 2 - 重複步驟 3-5,直到 E 不再減少,或者聚類成員資格不再改變。
步驟 3 - 對於每個輸入向量ip,其中p ∈ {1,…,n},將ip放入具有最近原型的聚類Cj*中,該原型具有以下關係:
$$|i_{p}\:-\:w_{j*}|\:\leq\:|i_{p}\:-\:w_{j}|,\:j\:\in \lbrace1,....,k\rbrace$$
步驟 4 - 對於每個聚類Cj,其中j ∈ { 1,…,k},更新原型wj為當前在Cj中所有樣本的質心,以便
$$w_{j}\:=\:\sum_{i_{p}\in C_{j}}\frac{i_{p}}{|C_{j}|}$$
步驟 5 - 計算總量化誤差如下:
$$E\:=\:\sum_{j=1}^k\sum_{i_{p}\in w_{j}}|i_{p}\:-\:w_{j}|^2$$
Neocognitron
它是一個多層前饋網路,由 Fukushima 於 20 世紀 80 年代開發。該模型基於監督學習,用於視覺模式識別,主要是手寫字元。它基本上是 Cognitron 網路的擴充套件,Cognitron 網路也是由 Fukushima 於 1975 年開發的。
架構
它是一個分層網路,包含許多層,並且這些層中存在區域性連線模式。
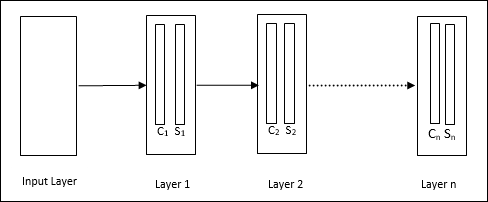
正如我們在上圖中看到的,neocognitron 被分成不同的連線層,每一層都有兩個單元。這些單元的解釋如下:
S 單元 - 它被稱為簡單單元,經過訓練可以響應特定模式或一組模式。
C 單元 - 它被稱為複雜單元,它結合了來自 S 單元的輸出,同時減少了每個陣列中的單元數量。換句話說,C 單元會置換 S 單元的輸出。
訓練演算法
Neocognitron 的訓練被發現是逐層進行的。從輸入層到第一層的權重被訓練並凍結。然後,訓練從第一層到第二層的權重,依此類推。S 單元和 C 單元之間的內部計算取決於來自前幾層的權重。因此,我們可以說訓練演算法取決於 S 單元和 C 單元上的計算。
S 單元中的計算
S 單元擁有從前一層接收的興奮性訊號,並擁有在同一層內獲得的抑制性訊號。
$$\theta=\:\sqrt{\sum\sum t_{i} c_{i}^2}$$
這裡,ti是固定權重,ci是來自 C 單元的輸出。
S 單元的縮放輸入可以計算如下:
$$x\:=\:\frac{1\:+\:e}{1\:+\:vw_{0}}\:-\:1$$
這裡,$e\:=\:\sum_i c_{i}w_{i}$
wi是從 C 單元到 S 單元的調整權重。
w0是輸入和 S 單元之間可調整的權重。
v是來自 C 單元的興奮性輸入。
輸出訊號的啟用為:
$$s\:=\:\begin{cases}x, & if\:x \geq 0\\0, & if\:x < 0\end{cases}$$
C 單元中的計算
C 層的淨輸入為
$$C\:=\:\displaystyle\sum\limits_i s_{i}x_{i}$$
這裡,si是來自 S 單元的輸出,xi是從 S 單元到 C 單元的固定權重。
最終輸出如下:
$$C_{out}\:=\:\begin{cases}\frac{C}{a+C}, & if\:C > 0\\0, & otherwise\end{cases}$$
這裡‘a’是取決於網路效能的引數。
學習向量量化
學習向量量化 (LVQ) 與向量量化 (VQ) 和 Kohonen 自組織對映 (KSOM) 不同,它基本上是一個使用監督學習的競爭網路。我們可以將其定義為對模式進行分類的過程,其中每個輸出單元代表一個類別。由於它使用監督學習,因此網路將獲得一組具有已知分類的訓練模式以及輸出類別的初始分佈。完成訓練過程後,LVQ 將透過將其分配到與輸出單元相同的類別來對輸入向量進行分類。
架構
下圖顯示了 LVQ 的體系結構,它與 KSOM 的體系結構非常相似。我們可以看到,有“n”個輸入單元和“m”個輸出單元。各層完全互連,並帶有權重。
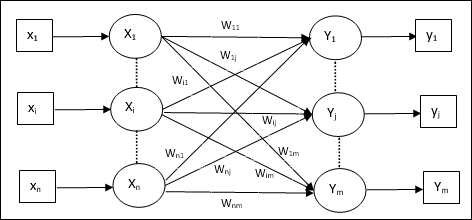
使用的引數
以下是 LVQ 訓練過程以及流程圖中使用的引數:
x = 訓練向量 (x1,...,xi,...,xn)
T = 訓練向量x的類別
wj = 第jth個輸出單元的權重向量
Cj = 與第jth個輸出單元相關的類別
訓練演算法
步驟 1 - 初始化參考向量,可以按如下方式完成:
步驟 1(a) - 從給定的訓練向量集中,取前“m”(聚類數)個訓練向量並將其用作權重向量。其餘向量可用於訓練。
步驟 1(b) - 隨機分配初始權重和分類。
步驟 1(c) - 應用 K 均值聚類方法。
步驟 2 - 初始化參考向量 $\alpha$
步驟 3 - 如果未滿足停止此演算法的條件,則繼續執行步驟 4-9。
步驟 4 - 對於每個訓練輸入向量x,執行步驟 5-6。
步驟 5 - 計算j = 1 到 m和i = 1 到 n的歐幾里得距離的平方
$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$
步驟 6 - 獲取獲勝單元J,其中D(j)最小。
步驟 7 − 使用以下關係計算獲勝單元的新權重 −
如果 T = Cj,則 $w_{j}(new)\:=\:w_{j}(old)\:+\:\alpha[x\:-\:w_{j}(old)]$
如果 T ≠ Cj,則 $w_{j}(new)\:=\:w_{j}(old)\:-\:\alpha[x\:-\:w_{j}(old)]$
步驟 8 − 降低學習率 $\alpha$。
步驟 9 − 測試停止條件。它可能是如下所示 −
- 達到最大迭代次數。
- 學習率降低到可忽略不計的值。
流程圖
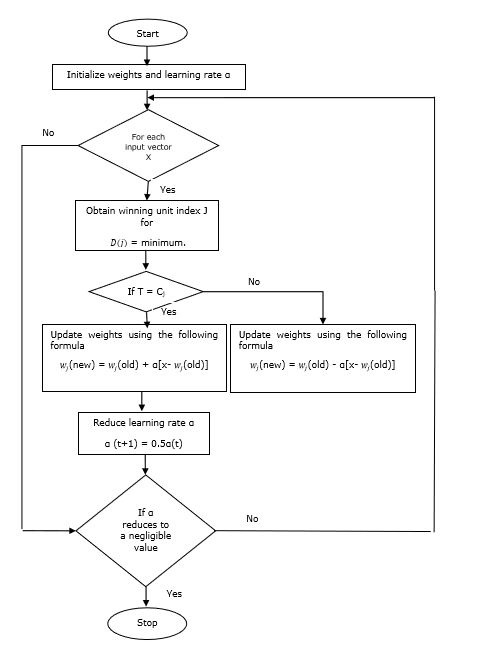
變體
Kohonen 開發了另外三個變體,即 LVQ2、LVQ2.1 和 LVQ3。由於獲勝單元和亞軍單元都會學習,這三個變體的複雜度都高於 LVQ。
LVQ2
如上所述,LVQ 其他變體的概念是由視窗構成的。此視窗將基於以下引數 −
x − 當前輸入向量
yc − 最接近 x 的參考向量
yr − 另一個參考向量,它是次接近 x 的向量
dc − 從 x 到 yc 的距離
dr − 從 x 到 yr 的距離
如果輸入向量 x 落入視窗內,則
$$\frac{d_{c}}{d_{r}}\:>\:1\:-\:\theta\:\:and\:\:\frac{d_{r}}{d_{c}}\:>\:1\:+\:\theta$$
這裡,$\theta$ 是訓練樣本的數量。
可以使用以下公式進行更新 −
$y_{c}(t\:+\:1)\:=\:y_{c}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c}(t)]$ (屬於不同類別)
$y_{r}(t\:+\:1)\:=\:y_{r}(t)\:+\:\alpha(t)[x(t)\:-\:y_{r}(t)]$ (屬於同一類別)
這裡$\alpha$是學習率。
LVQ2.1
在 LVQ2.1 中,我們將取兩個最接近的向量,即 yc1 和 yc2,視窗條件如下 −
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)$$
$$Max\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:<\:(1\:+\:\theta)$$
可以使用以下公式進行更新 −
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c1}(t)]$ (屬於不同類別)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c2}(t)]$ (屬於同一類別)
這裡,$\alpha$ 是學習率。
LVQ3
在 LVQ3 中,我們將取兩個最接近的向量,即 yc1 和 yc2,視窗條件如下 −
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)(1\:+\:\theta)$$
這裡 $\theta\approx 0.2$
可以使用以下公式進行更新 −
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\beta(t)[x(t)\:-\:y_{c1}(t)]$ (屬於不同類別)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\beta(t)[x(t)\:-\:y_{c2}(t)]$ (屬於同一類別)
這裡 $\beta$ 是學習率 $\alpha$ 的倍數,並且 $\beta\:=\:m \alpha(t)$,對於每個 0.1 < m < 0.5
自適應諧振理論
該網路由 Stephen Grossberg 和 Gail Carpenter 於 1987 年開發。它基於競爭並使用無監督學習模型。自適應諧振理論 (ART) 網路顧名思義,始終對新學習開放(自適應),而不會丟失舊模式(諧振)。基本上,ART 網路是一個向量分類器,它接受一個輸入向量並將其分類到一個類別中,這取決於它最類似於哪個儲存模式。
工作原理
ART 分類的主要操作可以分為以下階段 −
識別階段 − 將輸入向量與輸出層每個節點上呈現的分類進行比較。如果神經元的輸出與應用的分類最佳匹配,則其輸出變為“1”,否則變為“0”。
比較階段 − 在此階段,將輸入向量與比較層向量進行比較。重置條件是相似度小於警戒引數。
搜尋階段 − 在此階段,網路將搜尋上述階段中完成的重置和匹配。因此,如果沒有重置並且匹配相當好,則分類完成。否則,將重複該過程,並且必須傳送其他儲存模式以找到正確的匹配。
ART1
它是一種 ART 型別,旨在聚類二進位制向量。我們可以透過其架構來了解這一點。
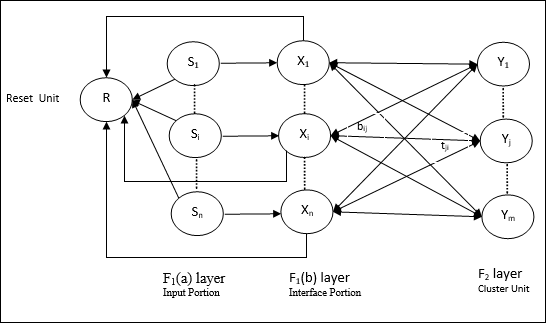
ART1 的架構
它包含以下兩個單元 −
計算單元 − 它由以下部分組成 −
輸入單元 (F1 層) − 它進一步具有以下兩個部分 −
F1(a) 層(輸入部分) − 在 ART1 中,除了只有輸入向量之外,此部分沒有處理。它連線到 F1(b) 層(介面部分)。
F1(b) 層(介面部分) − 此部分將來自輸入部分的訊號與 F2 層的訊號組合。F1(b) 層透過自下而上的權重 bij 連線到 F2 層,F2 層透過自上而下的權重 tji 連線到 F1(b) 層。
聚類單元 (F2 層) − 這是一個競爭層。選擇具有最大淨輸入的單元來學習輸入模式。所有其他聚類單元的啟用都設定為 0。
重置機制 − 此機制的工作基於自上而下的權重和輸入向量之間的相似性。現在,如果這種相似程度小於警戒引數,則不允許聚類學習模式,並且會發生重置。
補充單元 − 實際上,重置機制的問題在於,F2 層必須在某些條件下被抑制,並且在發生某些學習時也必須可用。這就是為什麼添加了兩個補充單元,即 G1 和 G2,以及重置單元 R。它們被稱為增益控制單元。這些單元接收並向網路中存在的其他單元傳送訊號。“+”表示興奮性訊號,“−”表示抑制性訊號。
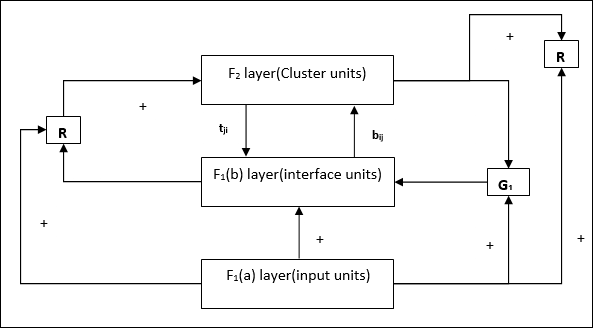
使用的引數
使用以下引數 −
n − 輸入向量中分量的數量
m − 可以形成的最大聚類數
bij − 從 F1(b) 到 F2 層的權重,即自下而上的權重
tji − 從 F2 到 F1(b) 層的權重,即自上而下的權重
ρ − 警戒引數
||x|| − 向量 x 的範數
演算法
步驟 1 − 初始化學習率、警戒引數和權重,如下所示 −
$$\alpha\:>\:1\:\:and\:\:0\:<\rho\:\leq\:1$$
$$0\:<\:b_{ij}(0)\:<\:\frac{\alpha}{\alpha\:-\:1\:+\:n}\:\:and\:\:t_{ij}(0)\:=\:1$$
步驟 2 − 當停止條件不為真時,繼續步驟 3-9。
步驟 3 − 對於每個訓練輸入,繼續步驟 4-6。
步驟 4 − 設定所有 F1(a) 和 F1 單元的啟用,如下所示
F2 = 0 和 F1(a) = 輸入向量
步驟 5 − 來自 F1(a) 到 F1(b) 層的輸入訊號必須像這樣傳送
$$s_{i}\:=\:x_{i}$$
步驟 6 − 對於每個被抑制的 F2 節點
$y_{j}\:=\:\sum_i b_{ij}x_{i}$ 條件是 yj ≠ -1
步驟 7 − 當重置為真時,執行步驟 8-10。
步驟 8 − 找到 J,對於所有節點 j,yJ ≥ yj
步驟 9 − 再次計算 F1(b) 上的啟用,如下所示
$$x_{i}\:=\:sitJi$$
步驟 10 − 現在,在計算向量 x 和向量 s 的範數後,我們需要檢查重置條件,如下所示 −
如果 ||x||/ ||s|| < 警戒引數 ρ,則抑制節點 J 並轉到步驟 7
否則如果 ||x||/ ||s|| ≥ 警戒引數 ρ,則繼續。
步驟 11 − 節點 J 的權重更新可以如下進行 −
$$b_{ij}(new)\:=\:\frac{\alpha x_{i}}{\alpha\:-\:1\:+\:||x||}$$
$$t_{ij}(new)\:=\:x_{i}$$
步驟 12 − 必須檢查演算法的停止條件,它可能是如下所示 −
- 權重沒有任何變化。
- 未對單元執行重置。
- 達到最大迭代次數。
Kohonen自組織特徵對映
假設我們有一些任意維度的模式,但是我們需要將它們轉換為一維或二維。然後,特徵對映過程對於將寬模式空間轉換為典型的特徵空間非常有用。現在,問題出現了,為什麼我們需要自組織特徵對映?原因是,除了能夠將任意維度轉換為一維或二維之外,它還必須具有保持鄰域拓撲的能力。
Kohonen SOM 中的鄰域拓撲
可以有多種拓撲結構,但是以下兩種拓撲結構使用得最多 −
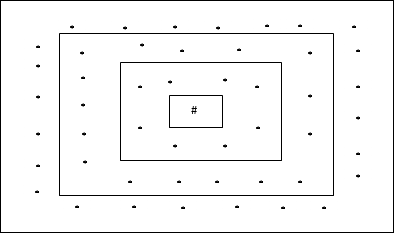
矩形網格拓撲
這種拓撲在距離 2 網格中具有 24 個節點,在距離 1 網格中具有 16 個節點,在距離 0 網格中具有 8 個節點,這意味著每個矩形網格之間的差值為 8 個節點。獲勝單元用 # 表示。
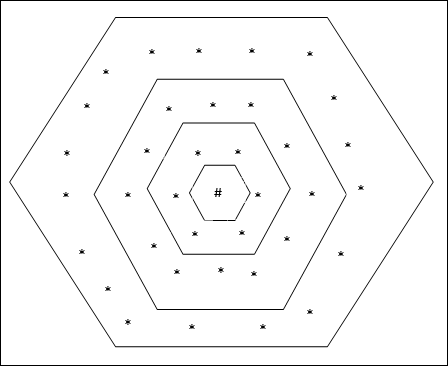
六邊形網格拓撲
這種拓撲在距離 2 網格中具有 18 個節點,在距離 1 網格中具有 12 個節點,在距離 0 網格中具有 6 個節點,這意味著每個矩形網格之間的差值為 6 個節點。獲勝單元用 # 表示。
架構
KSOM 的架構類似於競爭網路的架構。藉助前面討論的鄰域方案,可以在網路的擴充套件區域進行訓練。
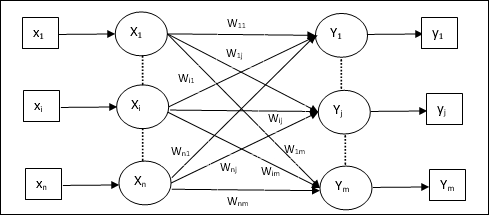
訓練演算法
步驟 1 − 初始化權重、學習率 α 和鄰域拓撲方案。
步驟 2 − 當停止條件不為真時,繼續步驟 3-9。
步驟 3 − 對於每個輸入向量 x,繼續步驟 4-6。
步驟 4 − 計算 j = 1 到 m 的歐幾里德距離的平方
$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n \displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$
步驟 5 − 獲取獲勝單元 J,其中 D(j) 最小。
步驟 6 − 使用以下關係計算獲勝單元的新權重 −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha[x_{i}\:-\:w_{ij}(old)]$$
步驟 7 − 使用以下關係更新學習率 α −
$$\alpha(t\:+\:1)\:=\:0.5\alpha t$$
步驟 8 − 減小拓撲方案的半徑。
步驟 9 − 檢查網路的停止條件。
聯想記憶網路
這些型別的神經網路基於模式關聯工作,這意味著它們可以儲存不同的模式,並且在輸出時,它們可以透過將它們與給定的輸入模式匹配來產生儲存的模式之一。這些型別的儲存器也稱為內容定址儲存器 (CAM)。聯想儲存器將儲存的模式作為資料檔案進行並行搜尋。
以下是我們可以觀察到的兩種型別的聯想儲存器 −
- 自聯想記憶
- 異聯想記憶
自聯想記憶
這是一個單層神經網路,其中輸入訓練向量和輸出目標向量相同。確定權重,以便網路儲存一組模式。
架構
如下圖所示,自聯想記憶網路的架構具有‘n’個輸入訓練向量和同樣數量的‘n’個輸出目標向量。
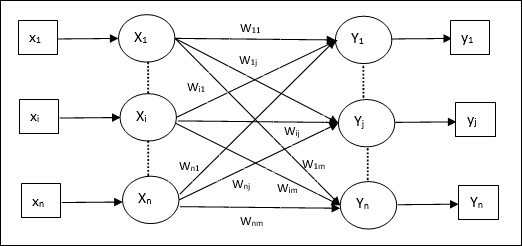
訓練演算法
該網路使用Hebb學習規則或Delta學習規則進行訓練。
步驟 1 − 將所有權重初始化為零,即wij = 0 (i = 1 到 n, j = 1 到 n)
步驟 2 − 對每個輸入向量執行步驟 3-4。
步驟 3 − 按如下方式啟用每個輸入單元:
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步驟 4 − 按如下方式啟用每個輸出單元:
$$y_{j}\:=\:s_{j}\:(j\:=\:1\:to\:n)$$
步驟 5 − 按如下方式調整權重:
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:x_{i}y_{j}$$
測試演算法
步驟 1 − 設定Hebb規則訓練期間獲得的權重。
步驟 2 − 對每個輸入向量執行步驟 3-5。
步驟 3 − 將輸入單元的啟用設定為與輸入向量相同。
步驟 4 − 計算每個輸出單元j = 1 到 n的淨輸入
$$y_{inj}\:=\:\displaystyle\sum\limits_{i=1}^n x_{i}w_{ij}$$
步驟 5 − 應用以下啟用函式來計算輸出
$$y_{j}\:=\:f(y_{inj})\:=\:\begin{cases}+1 & if\:y_{inj}\:>\:0\\-1 & if\:y_{inj}\:\leqslant\:0\end{cases}$$
異聯想記憶
與自聯想記憶網路類似,這也是一個單層神經網路。但是,在這個網路中,輸入訓練向量和輸出目標向量並不相同。權重被確定,以便網路儲存一組模式。異聯想網路本質上是靜態的,因此不會有非線性或延遲操作。
架構
如下圖所示,異聯想記憶網路的架構具有‘n’個輸入訓練向量和‘m’個輸出目標向量。
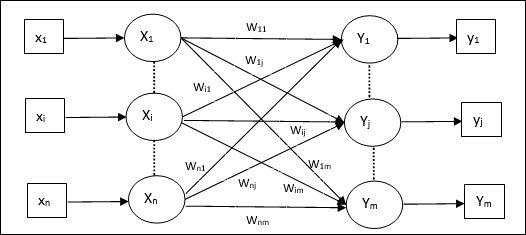
訓練演算法
該網路使用Hebb學習規則或Delta學習規則進行訓練。
步驟 1 − 將所有權重初始化為零,即wij = 0 (i = 1 到 n, j = 1 到 m)
步驟 2 − 對每個輸入向量執行步驟 3-4。
步驟 3 − 按如下方式啟用每個輸入單元:
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
步驟 4 − 按如下方式啟用每個輸出單元:
$$y_{j}\:=\:s_{j}\:(j\:=\:1\:to\:m)$$
步驟 5 − 按如下方式調整權重:
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:x_{i}y_{j}$$
測試演算法
步驟 1 − 設定Hebb規則訓練期間獲得的權重。
步驟 2 − 對每個輸入向量執行步驟 3-5。
步驟 3 − 將輸入單元的啟用設定為與輸入向量相同。
步驟 4 − 計算每個輸出單元j = 1 到 m的淨輸入:
$$y_{inj}\:=\:\displaystyle\sum\limits_{i=1}^n x_{i}w_{ij}$$
步驟 5 − 應用以下啟用函式來計算輸出
$$y_{j}\:=\:f(y_{inj})\:=\:\begin{cases}+1 & if\:y_{inj}\:>\:0\\0 & if\:y_{inj}\:=\:0\\-1 & if\:y_{inj}\:<\:0\end{cases}$$
人工神經網路 - Hopfield網路
Hopfield神經網路由John J. Hopfield博士於1982年發明。它由單層組成,包含一個或多個完全連線的迴圈神經元。Hopfield網路通常用於自關聯和最佳化任務。
離散Hopfield網路
Hopfield網路以離散的方式執行,換句話說,可以認為輸入和輸出模式是離散向量,其性質可以是二進位制(0,1)或雙極性(+1, -1)。該網路具有對稱權重,沒有自連線,即wij = wji和wii = 0。
架構
以下是一些關於離散Hopfield網路需要注意的重要事項:
該模型由具有一個反相輸出和一個非反相輸出的神經元組成。
每個神經元的輸出應該是其他神經元的輸入,但不能是自身的輸入。
權重/連線強度由wij表示。
連線可以是興奮性的,也可以是抑制性的。如果神經元的輸出與其輸入相同,則為興奮性,否則為抑制性。
權重應是對稱的,即wij = wji
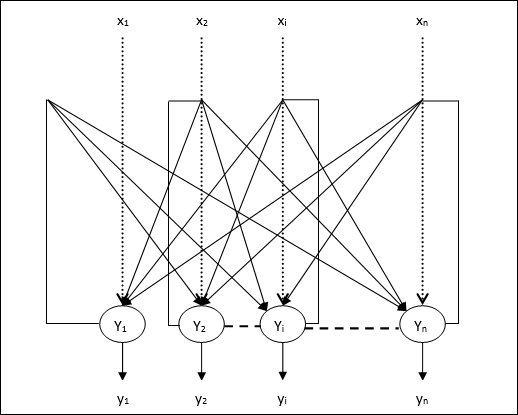
從Y1到Y2、Yi和Yn的輸出分別具有權重w12、w1i和w1n。類似地,其他弧線也具有其上的權重。
訓練演算法
在離散Hopfield網路的訓練過程中,權重將被更新。眾所周知,我們可以具有二進位制輸入向量和雙極性輸入向量。因此,在這兩種情況下,權重更新都可以透過以下關係完成
情況 1 − 二進位制輸入模式
對於一組二進位制模式s(p), p = 1 到 P
這裡,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
權重矩陣由下式給出
$$w_{ij}\:=\:\sum_{p=1}^P[2s_{i}(p)-\:1][2s_{j}(p)-\:1]\:\:\:\:\:for\:i\:\neq\:j$$
情況 2 − 雙極性輸入模式
對於一組二進位制模式s(p), p = 1 到 P
這裡,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
權重矩陣由下式給出
$$w_{ij}\:=\:\sum_{p=1}^P[s_{i}(p)][s_{j}(p)]\:\:\:\:\:for\:i\:\neq\:j$$
測試演算法
步驟 1 − 初始化權重,這些權重是透過使用Hebbian原理從訓練演算法中獲得的。
步驟 2 − 如果網路的啟用未穩定,則執行步驟 3-9。
步驟 3 − 對於每個輸入向量X,執行步驟 4-8。
步驟 4 − 將網路的初始啟用設定為等於外部輸入向量X,如下所示:
$$y_{i}\:=\:x_{i}\:\:\:for\:i\:=\:1\:to\:n$$
步驟 5 − 對於每個單元Yi,執行步驟 6-9。
步驟 6 − 按如下方式計算網路的淨輸入:
$$y_{ini}\:=\:x_{i}\:+\:\displaystyle\sum\limits_{j}y_{j}w_{ji}$$
步驟 7 − 對淨輸入應用以下啟用函式來計算輸出:
$$y_{i}\:=\begin{cases}1 & if\:y_{ini}\:>\:\theta_{i}\\y_{i} & if\:y_{ini}\:=\:\theta_{i}\\0 & if\:y_{ini}\:<\:\theta_{i}\end{cases}$$
這裡$\theta_{i}$是閾值。
步驟 8 − 將此輸出yi廣播到所有其他單元。
步驟 9 − 測試網路的連線。
能量函式評估
能量函式定義為系統的狀態的有界且非遞增函式。
能量函式Ef,也稱為Lyapunov函式,確定離散Hopfield網路的穩定性,其特徵如下:
$$E_{f}\:=\:-\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^n y_{i}y_{j}w_{ij}\:-\:\displaystyle\sum\limits_{i=1}^n x_{i}y_{i}\:+\:\displaystyle\sum\limits_{i=1}^n \theta_{i}y_{i}$$
條件 − 在穩定網路中,每當節點狀態發生變化時,上述能量函式都會減小。
假設當節點i的狀態從$y_i^{(k)}$變為$y_i^{(k\:+\:1)}$時,能量變化$\Delta E_{f}$由以下關係給出
$$\Delta E_{f}\:=\:E_{f}(y_i^{(k+1)})\:-\:E_{f}(y_i^{(k)})$$
$$=\:-\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{ij}y_i^{(k)}\:+\:x_{i}\:-\:\theta_{i}\end{array}\right)(y_i^{(k+1)}\:-\:y_i^{(k)})$$
$$=\:-\:(net_{i})\Delta y_{i}$$
這裡$\Delta y_{i}\:=\:y_i^{(k\:+\:1)}\:-\:y_i^{(k)}$
能量變化取決於一次只有一個單元可以更新其啟用這一事實。
連續Hopfield網路
與離散Hopfield網路相比,連續網路具有連續變數的時間。它也用於自關聯和最佳化問題,例如旅行商問題。
模型 − 可以透過新增電子元件(例如放大器)來構建模型或架構,這些元件可以將輸入電壓對映到透過S型啟用函式的輸出電壓。
能量函式評估
$$E_f = \frac{1}{2}\displaystyle\sum\limits_{i=1}^n\sum_{\substack{j = 1\\ j \ne i}}^n y_i y_j w_{ij} - \displaystyle\sum\limits_{i=1}^n x_i y_i + \frac{1}{\lambda} \displaystyle\sum\limits_{i=1}^n \sum_{\substack{j = 1\\ j \ne i}}^n w_{ij} g_{ri} \int_{0}^{y_i} a^{-1}(y) dy$$
這裡λ是增益引數,gri是輸入電導。
玻爾茲曼機
這些是具有遞迴結構的隨機學習過程,是ANN中使用的早期最佳化技術的基礎。Boltzmann機由Geoffrey Hinton和Terry Sejnowski於1985年發明。Hinton關於Boltzmann機的論述可以使我們更加清晰地理解。
“這個網路的一個令人驚訝的特點是它只使用區域性可用的資訊。權重的變化只取決於它連線的兩個單元的行為,即使變化最佳化的是全域性度量” - Ackley, Hinton 1985。
關於Boltzmann機的一些重要要點:
它們使用遞迴結構。
它們由隨機神經元組成,這些神經元具有兩種可能狀態之一,即1或0。
其中一些神經元是自適應的(自由狀態),而另一些神經元是固定的(凍結狀態)。
如果我們將模擬退火應用於離散Hopfield網路,那麼它將成為Boltzmann機。
Boltzmann機的目標
Boltzmann機的主要目的是最佳化問題的解決方案。Boltzmann機的工作是最佳化權重以及與該特定問題相關的數量。
架構
下圖顯示了Boltzmann機的架構。從圖中可以清楚地看出,它是一個二維單元陣列。這裡,單元之間互連上的權重為–p,其中p > 0。自連線的權重由b給出,其中b > 0。
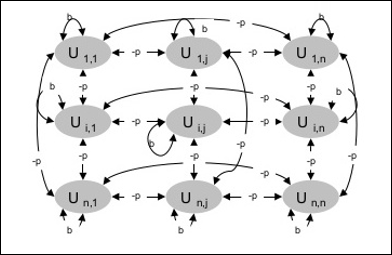
訓練演算法
眾所周知,Boltzmann機具有固定權重,因此不需要訓練演算法,因為我們不需要更新網路中的權重。但是,為了測試網路,我們必須設定權重以及找到一致性函式(CF)。
Boltzmann機有一組單元Ui和Uj,並在其上具有雙向連線。
我們考慮固定權重,例如wij。
如果Ui和Uj連線,則wij ≠ 0。
加權互連中也存在對稱性,即wij = wji。
wii也存在,即單元之間存在自連線。
對於任何單元Ui,其狀態ui將為1或0。
Boltzmann機的主要目標是最大化一致性函式(CF),這可以透過以下關係給出
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
現在,當狀態從1變為0或從0變為1時,一致性的變化可以透過以下關係給出:
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
這裡ui是Ui的當前狀態。
係數(1 - 2ui)的變化由以下關係給出:
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:is\:currently\:off\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
通常,單元Ui不會改變其狀態,但如果改變,則資訊將駐留在單元本地。隨著這種變化,網路的一致性也會增加。
網路接受單元狀態變化的機率由以下關係給出:
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
這裡,T 是控制引數。當 CF 達到最大值時,它會減小。
測試演算法
步驟1 − 初始化以下內容以開始訓練:
- 表示問題約束的權重
- 控制引數 T
步驟 2 − 當停止條件不滿足時,繼續步驟 3-8。
步驟 3 − 執行步驟 4-7。
步驟 4 − 假設其中一個狀態改變了權重,並隨機選擇整數I, J,其值介於1 和 n 之間。
步驟 5 − 計算一致性變化如下:
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
步驟 6 − 計算該網路接受狀態變化的機率
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
步驟 7 − 如下接受或拒絕此更改:
情況一 − 如果 R < AF,則接受更改。
情況二 − 如果 R ≥ AF,則拒絕更改。
這裡,R 是介於 0 和 1 之間的隨機數。
步驟 8 − 如下減少控制引數(溫度):
T(新) = 0.95T(舊)
步驟 9 − 測試停止條件,這些條件可能是:
- 溫度達到指定值
- 在指定的迭代次數內沒有狀態變化
盒中腦狀態網路
盒中腦狀態 (BSB) 神經網路是一個非線性自關聯神經網路,可以擴充套件到具有兩層或更多層的異關聯。它也類似於 Hopfield 網路。它由 J.A. Anderson、J.W. Silverstein、S.A. Ritz 和 R.S. Jones 於 1977 年提出。
關於 BSB 網路的一些重要要點:
它是一個完全連線的網路,節點的最大數量取決於輸入空間的維數n。
所有神經元同時更新。
神經元取值範圍為 -1 到 +1。
數學公式
BSB 網路中使用的節點函式是斜坡函式,可以定義如下:
$$f(net)\:=\:min(1,\:max(-1,\:net))$$
此斜坡函式是有界且連續的。
眾所周知,每個節點都會改變其狀態,這可以透過以下數學關係來實現:
$$x_{t}(t\:+\:1)\:=\:f\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{i,j}x_{j}(t)\end{array}\right)$$
這裡,xi(t) 是ith 節點在時間t 的狀態。
從ith 節點到jth 節點的權重可以用以下關係來衡量:
$$w_{ij}\:=\:\frac{1}{P}\displaystyle\sum\limits_{p=1}^P (v_{p,i}\:v_{p,j})$$
這裡,P 是訓練模式的數量,這些模式是雙極的。
使用Hopfield網路進行最佳化
最佳化是使設計、情況、資源和系統等儘可能有效的一種行為。利用代價函式和能量函式之間的相似性,我們可以使用高度互連的神經元來解決最佳化問題。這種神經網路是 Hopfield 網路,它由單層組成,包含一個或多個完全連線的迴圈神經元。這可用於最佳化。
使用 Hopfield 網路進行最佳化時需要注意的幾點:
能量函式必須是網路的最小值。
它將找到令人滿意的解決方案,而不是從儲存的模式中選擇一個。
Hopfield 網路找到的解決方案的質量在很大程度上取決於網路的初始狀態。
旅行商問題
尋找旅行商旅行的最短路線是可以透過使用 Hopfield 神經網路進行最佳化的計算問題之一。
TSP 的基本概念
旅行商問題 (TSP) 是一種經典的最佳化問題,其中一名銷售人員必須前往n 個相互連線的城市,同時保持成本和行駛距離最小。例如,銷售人員必須前往一組 4 個城市 A、B、C、D,目標是找到最短的環形路線 A-B-C-D,以最大限度地降低成本,其中還包括從最後一個城市 D 到第一個城市 A 的旅行成本。
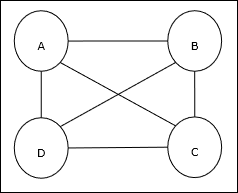
矩陣表示
實際上,n 城市 TSP 的每個路線都可以表示為n × n 矩陣,其ith 行描述ith 城市的位置。對於 4 個城市 A、B、C、D,該矩陣M 可以表示如下:
$$M = \begin{bmatrix}A: & 1 & 0 & 0 & 0 \\B: & 0 & 1 & 0 & 0 \\C: & 0 & 0 & 1 & 0 \\D: & 0 & 0 & 0 & 1 \end{bmatrix}$$
Hopfield 網路的解決方案
在考慮 Hopfield 網路對此 TSP 的解決方案時,網路中的每個節點都對應於矩陣中的一個元素。
能量函式計算
為了成為最佳化的解決方案,能量函式必須最小。基於以下約束,我們可以計算能量函式如下:
約束 I
第一個約束,我們將根據它計算能量函式,是矩陣M 的每一行中必須有一個元素等於 1,而每一行中的其他元素必須等於0,因為每個城市在 TSP 路線中只能出現一個位置。此約束可以用數學方式寫成如下:
$$\displaystyle\sum\limits_{j=1}^n M_{x,j}\:=\:1\:for \: x\:\in \:\lbrace1,...,n\rbrace$$
現在,基於上述約束要最小化的能量函式將包含一個與以下成比例的項:
$$\displaystyle\sum\limits_{x=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{j=1}^n M_{x,j}\end{array}\right)^2$$
約束 II
眾所周知,在 TSP 中,一個城市可以出現在路線中的任何位置,因此在矩陣M 的每一列中,必須有一個元素等於 1,而其他元素必須等於 0。此約束可以用數學方式寫成如下:
$$\displaystyle\sum\limits_{x=1}^n M_{x,j}\:=\:1\:for \: j\:\in \:\lbrace1,...,n\rbrace$$
現在,基於上述約束要最小化的能量函式將包含一個與以下成比例的項:
$$\displaystyle\sum\limits_{j=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x=1}^n M_{x,j}\end{array}\right)^2$$
成本函式計算
假設一個用C 表示的 (n × n) 方陣表示n 個城市(其中n > 0)的 TSP 成本矩陣。計算成本函式時,以下是一些引數:
Cx, y − 成本矩陣的元素表示從城市x 到y 的旅行成本。
A 和 B 的元素的鄰接性可以用以下關係表示:
$$M_{x,i}\:=\:1\:\: and\:\: M_{y,i\pm 1}\:=\:1$$
眾所周知,在矩陣中,每個節點的輸出值可以是 0 或 1,因此對於每對城市 A、B,我們可以將以下項新增到能量函式中:
$$\displaystyle\sum\limits_{i=1}^n C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})$$
基於上述成本函式和約束值,最終能量函式E 可以表示為:
$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{x}\displaystyle\sum\limits_{y\neq x}C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})\:+$$
$$\:\begin{bmatrix}\gamma_{1} \displaystyle\sum\limits_{x} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{i} M_{x,i}\end{array}\right)^2\:+\: \gamma_{2} \displaystyle\sum\limits_{i} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x} M_{x,i}\end{array}\right)^2 \end{bmatrix}$$
這裡,γ1 和γ2 是兩個加權常數。
其他最佳化技術
迭代梯度下降法
梯度下降,也稱為最速下降,是一種迭代最佳化演算法,用於查詢函式的區域性最小值。在最小化函式時,我們關注的是要最小化的成本或誤差(記住旅行商問題)。它廣泛用於深度學習,這在各種情況下都非常有用。這裡要記住的是,我們關注的是區域性最佳化,而不是全域性最佳化。
主要工作原理
我們可以透過以下步驟瞭解梯度下降的主要工作原理:
首先,從解決方案的初始猜測開始。
然後,取該點的函式梯度。
之後,透過在梯度的負方向上逐步調整解決方案來重複此過程。
透過遵循上述步驟,演算法最終將收斂到梯度為零的位置。
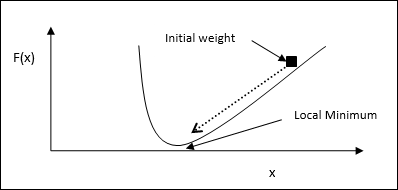
數學概念
假設我們有一個函式f(x),我們試圖找到這個函式的最小值。以下是查詢f(x) 最小值的步驟。
首先,為 x 給出一些初始值 $x_{0}$
現在取函式的梯度 $\nabla f$,其直覺是梯度將給出該 x 處曲線的斜率,其方向將指向函式的增加,以找出最小化它的最佳方向。
現在更改 x 如下:
$$x_{n\:+\:1}\:=\:x_{n}\:-\:\theta \nabla f(x_{n})$$
這裡,θ > 0 是訓練率(步長),它迫使演算法採取小跳躍。
估計步長
實際上,錯誤的步長θ 可能無法達到收斂,因此仔細選擇步長非常重要。選擇步長時必須記住以下幾點
不要選擇太大的步長,否則會產生負面影響,即它會發散而不是收斂。
不要選擇太小的步長,否則它會花費大量時間才能收斂。
關於選擇步長的一些選項:
一種選擇是選擇固定的步長。
另一種選擇是為每次迭代選擇不同的步長。
模擬退火
模擬退火 (SA) 的基本概念源於固體中的退火。在退火過程中,如果我們將金屬加熱到其熔點以上並冷卻下來,則結構特性將取決於冷卻速度。我們也可以說 SA 模擬了退火冶金過程。
在 ANN 中的使用
SA 是一種隨機計算方法,其靈感來自退火比擬,用於逼近給定函式的全域性最佳化。我們可以使用 SA 來訓練前饋神經網路。
演算法
步驟 1 − 生成隨機解決方案。
步驟 2 − 使用某個成本函式計算其成本。
步驟 3 − 生成隨機相鄰解決方案。
步驟 4 − 使用相同的成本函式計算新解決方案成本。
步驟 5 − 如下比較新解決方案的成本與舊解決方案的成本:
如果新解決方案成本 < 舊解決方案成本,則轉到新解決方案。
步驟 6 − 測試停止條件,這可能是達到最大迭代次數或獲得可接受的解決方案。
人工神經網路 - 遺傳演算法
自然界一直是全人類靈感的重要源泉。遺傳演算法 (GA) 是基於自然選擇和遺傳概念的搜尋演算法。遺傳演算法是進化計算這個更大計算分支的一個子集。
遺傳演算法由 John Holland 及其在密歇根大學的學生和同事(最著名的是 David E. Goldberg)開發,此後已在各種最佳化問題上進行了嘗試,並取得了高度的成功。
在遺傳演算法中,我們有一組或一個種群的可能解來解決給定的問題。然後,這些解會進行重組和變異(就像在自然遺傳中一樣),產生新的後代,並且該過程在各個世代中重複。每個個體(或候選解)都被賦予一個適應度值(基於其目標函式值),適應度較高的個體有更高的機會交配併產生更“適應”的個體。這與達爾文的“適者生存”理論相符。
透過這種方式,我們不斷進化出更好的個體或解決方案,直到達到停止標準。
遺傳演算法本質上是足夠隨機的,但是它們比隨機區域性搜尋(我們只是嘗試各種隨機解決方案,並跟蹤到目前為止最好的解決方案)的效能要好得多,因為它們也利用了歷史資訊。
遺傳演算法的優點
遺傳演算法具有多種優點,使其廣受歡迎。這些包括:
不需要任何導數資訊(對於許多現實世界的問題可能不可用)。
與傳統方法相比,速度更快,效率更高。
具有非常好的並行能力。
可以最佳化連續函式和離散函式以及多目標問題。
提供一系列“良好”的解決方案,而不僅僅是一個解決方案。
始終可以得到問題的答案,並且隨著時間的推移答案會越來越好。
當搜尋空間非常大並且涉及大量引數時非常有用。
遺傳演算法的侷限性
與任何技術一樣,遺傳演算法也有一些侷限性。這些包括:
遺傳演算法不適用於所有問題,特別是那些簡單且可以使用導數資訊的問題。
適應度值會被重複計算,這對於某些問題來說可能計算成本很高。
由於其隨機性,無法保證解決方案的最優性或質量。
如果實現不當,遺傳演算法可能無法收斂到最優解。
遺傳演算法——動機
遺傳演算法能夠“足夠快”地提供“足夠好”的解決方案。這使得遺傳演算法在解決最佳化問題方面具有吸引力。需要遺傳演算法的原因如下:
解決難題
在計算機科學中,有一大類問題是NP-Hard的。這實際上意味著,即使是最強大的計算系統也需要很長時間(甚至數年!)才能解決該問題。在這種情況下,遺傳演算法被證明是提供可用的近似最優解的有效工具。
基於梯度的方法的失敗
傳統的基於微積分的方法的工作原理是從一個隨機點開始,沿著梯度的方向移動,直到到達山頂。這種技術效率很高,並且非常適用於單峰目標函式,例如線性迴歸中的成本函式。但是,在大多數現實世界的情況下,我們面臨一個非常複雜的問題,稱為景觀,由許多峰和許多谷組成,這會導致此類方法失敗,因為它們具有固有的陷入區域性最優的傾向,如下圖所示。
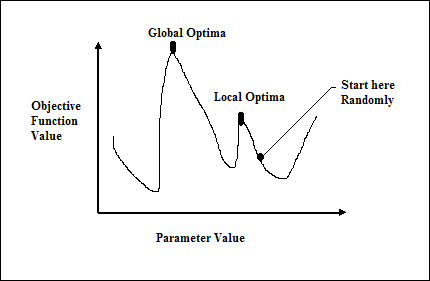
快速獲得良好的解決方案
旅行商問題 (TSP) 等一些難題具有現實世界的應用,例如路徑查詢和 VLSI 設計。現在假設您正在使用 GPS 導航系統,並且它需要幾分鐘(甚至幾小時)才能計算出從起點到目的地的“最佳”路徑。這種現實世界應用中的延遲是不可接受的,因此需要“足夠好”且“快速”交付的解決方案。
如何將遺傳演算法用於最佳化問題?
我們已經知道,最佳化是使設計、情況、資源和系統儘可能有效的一種行為。最佳化過程如下圖所示。

用於最佳化過程的遺傳演算法機制的階段
以下是將遺傳演算法用於問題最佳化時的階段。
隨機生成初始種群。
選擇具有最佳適應度值的初始解。
使用變異和交叉運算元重組所選解。
將後代插入種群。
現在,如果滿足停止條件,則返回具有最佳適應度值的解。否則,轉到步驟 2。
神經網路的應用
在研究 ANN 被廣泛使用的領域之前,我們需要了解為什麼 ANN 會成為首選的應用。
為什麼選擇人工神經網路?
我們需要透過人類的例子來理解上述問題的答案。孩提時代,我們依靠長輩(包括父母或老師)的幫助來學習。然後,透過自學或練習,我們終身學習。科學家和研究人員也正在使機器像人類一樣變得智慧,而 ANN 正因以下原因在其中發揮著非常重要的作用:
藉助神經網路,我們可以找到那些演算法方法成本過高或不存在的問題的解決方案。
神經網路可以透過示例學習,因此我們不需要對其進行太多程式設計。
神經網路的精度和速度比傳統速度顯著提高。
應用領域
以下是 ANN 正在使用的一些領域。這表明 ANN 在其發展和應用中具有跨學科的方法。
語音識別
語音在人際互動中佔據突出地位。因此,人們自然希望計算機具有語音介面。在當今時代,為了與機器進行通訊,人類仍然需要複雜的語言,這些語言難以學習和使用。為了減輕這種溝通障礙,一個簡單的解決方案可能是使用機器能夠理解的口語進行溝通。
這一領域已經取得了長足的進步,但是,此類系統仍然面臨詞彙量或語法有限的問題,以及在不同條件下為不同的說話者重新訓練系統的問題。ANN 在這個領域發揮著重要作用。以下 ANN 已用於語音識別:
多層網路
具有遞迴連線的多層網路
Kohonen 自組織特徵對映
最實用的網路是 Kohonen 自組織特徵對映,其輸入是語音波形的短片段。它將把相同型別的音素對映到輸出陣列,稱為特徵提取技術。提取特徵後,藉助一些聲學模型作為後端處理,它將識別話語。
字元識別
這是一個有趣的問題,屬於模式識別的一般領域。許多神經網路已被開發用於自動識別手寫字元,無論是字母還是數字。以下是已用於字元識別的一些 ANN:
- 多層神經網路,例如反向傳播神經網路。
- Neocognitron
儘管反向傳播神經網路具有多個隱藏層,但從一層到下一層的連線模式是區域性的。類似地,neocognitron 也具有多個隱藏層,其訓練是針對此類應用逐層進行的。
簽名驗證應用
簽名是在法律交易中授權和驗證人員的最有用方法之一。簽名驗證技術是一種非視覺技術。
對於此應用,第一種方法是提取特徵,或者更確切地說,是表示簽名的幾何特徵集。使用這些特徵集,我們必須使用高效的神經網路演算法訓練神經網路。在驗證階段,這個訓練好的神經網路將把簽名分類為真實或偽造。
人臉識別
這是識別給定面部的生物識別方法之一。由於“非面部”影像的特徵,這是一項典型的任務。但是,如果神經網路經過良好訓練,則可以將其分為兩類:具有面部的影像和不具有面部的影像。
首先,必須預處理所有輸入影像。然後,必須降低該影像的維數。最後,必須使用神經網路訓練演算法對其進行分類。以下神經網路用於使用預處理影像進行訓練:
使用反向傳播演算法訓練的全連線多層前饋神經網路。
對於降維,使用主成分分析 (PCA)。