玻爾茲曼機

這些是具有遞迴結構的隨機學習過程，是ANN早期最佳化技術的基礎。玻爾茲曼機由Geoffrey Hinton和Terry Sejnowski於1985年發明。Hinton對玻爾茲曼機的論述可以提供更清晰的理解。

“這個網路的一個令人驚訝的特點是它只使用區域性可用的資訊。權重的變化只取決於它連線的兩個單元的行為，即使這種變化最佳化的是一個全域性度量” - Ackley, Hinton 1985。

關於玻爾茲曼機的一些重要點：

玻爾茲曼機的目標

玻爾茲曼機的主要目的是最佳化問題的解決方案。玻爾茲曼機的工作是最佳化與特定問題相關的權重和數量。

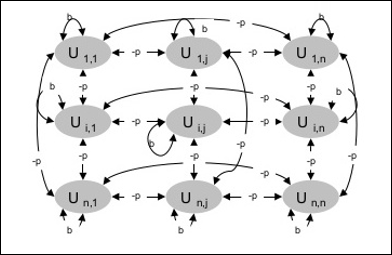
下圖顯示了玻爾茲曼機的架構。從圖中可以清楚地看出，它是一個二維單元陣列。這裡，單元之間互連上的權重為–p，其中p > 0。自連線的權重由b給出，其中b > 0。

眾所周知，玻爾茲曼機具有固定的權重，因此不需要訓練演算法，因為我們不需要更新網路中的權重。但是，要測試網路，我們必須設定權重以及找到共識函式 (CF)。

玻爾茲曼機有一組單元U_i和U_j，並且在它們之間具有雙向連線。

玻爾茲曼機的主要目標是最大化共識函式 (CF)，其關係如下所示

$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$

現在，當狀態從1變為0或從0變為1時，共識的變化可以透過以下關係給出：

$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$

這裡u_i是U_i的當前狀態。

係數 (1 - 2u_i) 的變化由以下關係給出：

$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:當前處於關閉狀態\\-1, & U_{i}\:當前處於開啟狀態\end{cases}$$

通常，單元U_i不會改變其狀態，但如果改變，則資訊將駐留在單元的本地。隨著這種變化，網路的共識也會增加。

網路接受單元狀態變化的機率由以下關係給出：

$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$

這裡，T是控制引數。當CF達到最大值時，它會減小。

步驟1 - 初始化以下內容以開始訓練：

步驟2 - 當停止條件不為真時，繼續步驟3-8。

步驟3 - 執行步驟4-7。

步驟4 - 假設其中一個狀態改變了權重，並將整數I, J選擇為1和n之間的隨機值。

步驟5 - 計算共識變化如下：

$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$

步驟6 - 計算網路接受狀態變化的機率

$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$

步驟7 - 接受或拒絕此更改，如下所示：

情況一 - 如果R < AF，則接受更改。

情況二 - 如果R ≥ AF，則拒絕更改。

這裡，R是0到1之間的隨機數。

步驟8 - 按如下方式減少控制引數（溫度）：

T(new) = 0.95T(old)

步驟9 - 測試停止條件，例如：

列印頁面