
學習向量量化
學習向量量化 (LVQ) 不同於向量量化 (VQ) 和 Kohonen 自組織對映 (KSOM),它本質上是一個使用監督學習的競爭網路。我們可以將其定義為對模式進行分類的過程,其中每個輸出單元代表一個類別。由於它使用監督學習,因此網路將獲得一組具有已知分類的訓練模式以及輸出類別的初始分佈。完成訓練過程後,LVQ 將透過將其分配到與輸出單元相同的類別來對輸入向量進行分類。
架構
下圖顯示了 LVQ 的架構,它與 KSOM 的架構非常相似。我們可以看到,有 “n” 個輸入單元和 “m” 個輸出單元。各層是完全互連的,並且在其上具有權重。
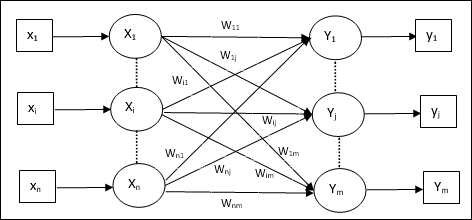
使用的引數
以下是 LVQ 訓練過程以及流程圖中使用的引數
x = 訓練向量 (x1,...,xi,...,xn)
T = 訓練向量 x 的類別
wj = 第 jth 個輸出單元的權重向量
Cj = 與第 jth 個輸出單元關聯的類別
訓練演算法
步驟 1 - 初始化參考向量,可以按如下方式進行 -
步驟 1(a) - 從給定的訓練向量集中,取前“m”(聚類數)個訓練向量並將其用作權重向量。其餘向量可用於訓練。
步驟 1(b) - 隨機分配初始權重和分類。
步驟 1(c) - 應用 K 均值聚類方法。
步驟 2 - 初始化參考向量 $\alpha$
步驟 3 - 如果未滿足停止此演算法的條件,則繼續執行步驟 4-9。
步驟 4 - 對於每個訓練輸入向量 x,執行步驟 5-6。
步驟 5 - 計算 j = 1 到 m 和 i = 1 到 n 的歐幾里得距離平方
$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$
步驟 6 - 獲取獲勝單元 J,其中 D(j) 最小。
步驟 7 - 透過以下關係計算獲勝單元的新權重 -
如果 T = Cj 則 $w_{j}(new)\:=\:w_{j}(old)\:+\:\alpha[x\:-\:w_{j}(old)]$
如果 T ≠ Cj 則 $w_{j}(new)\:=\:w_{j}(old)\:-\:\alpha[x\:-\:w_{j}(old)]$
步驟 8 - 降低學習率 $\alpha$。
步驟 9 - 測試停止條件。它可能是如下所示 -
- 達到最大迭代次數。
- 學習率降低到可忽略不計的值。
流程圖
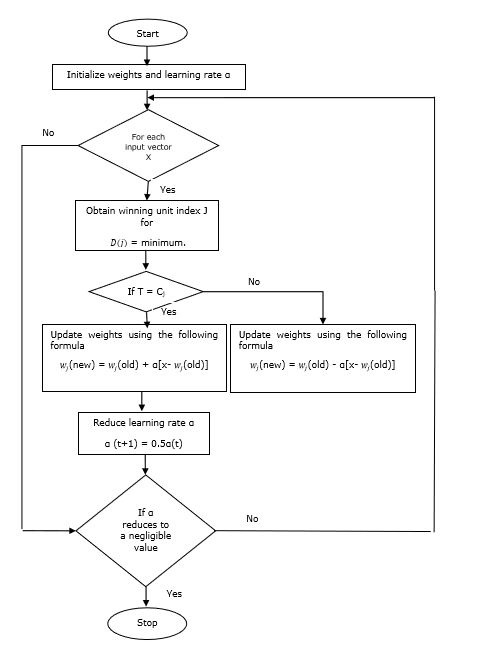
變體
Kohonen 開發了另外三種變體,即 LVQ2、LVQ2.1 和 LVQ3。由於獲勝單元和亞軍單元都將學習的概念,這三種變體的複雜性都高於 LVQ。
LVQ2
如上所述,LVQ 其他變體的概念,LVQ2 的條件是由視窗形成的。此視窗將基於以下引數 -
x - 當前輸入向量
yc - 最接近 x 的參考向量
yr - 另一個參考向量,它是次接近 x 的
dc - 從 x 到 yc 的距離
dr - 從 x 到 yr 的距離
如果輸入向量 x 位於視窗內,則
$$ \frac{d_{c}}{d_{r}}\:>\:1\:-\:\theta\:\:and\:\:\frac{d_{r}}{d_{c}}\:>\:1\:+\:\theta$$
這裡,$\theta$ 是訓練樣本的數量。
更新可以使用以下公式完成 -
$y_{c}(t\:+\:1)\:=\:y_{c}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c}(t)]$ (屬於不同的類別)
$y_{r}(t\:+\:1)\:=\:y_{r}(t)\:+\:\alpha(t)[x(t)\:-\:y_{r}(t)]$ (屬於相同的類別)
這裡 $\alpha$ 是學習率。
LVQ2.1
在 LVQ2.1 中,我們將採用兩個最接近的向量,即 yc1 和 yc2,視窗的條件如下 -
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)$$
$$Max\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:<\:(1\:+\:\theta)$$
更新可以使用以下公式完成 -
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c1}(t)]$ (屬於不同的類別)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c2}(t)]$ (屬於相同的類別)
這裡,$\alpha$ 是學習率。
LVQ3
在 LVQ3 中,我們將採用兩個最接近的向量,即 yc1 和 yc2,視窗的條件如下 -
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)(1\:+\:\theta)$$
這裡 $\theta\approx 0.2$
更新可以使用以下公式完成 -
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\beta(t)[x(t)\:-\:y_{c1}(t)]$ (屬於不同的類別)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\beta(t)[x(t)\:-\:y_{c2}(t)]$ (屬於相同的類別)
這裡 $\beta$ 是學習率 $\alpha$ 的倍數,並且 $\beta\:=\:m \alpha(t)$ 對於每個 0.1 < m < 0.5