Kohonen 自組織特徵對映

假設我們有一些任意維度的模式，但我們需要將它們轉換為一維或二維。那麼特徵對映的過程對於將寬模式空間轉換為典型的特徵空間非常有用。現在，問題出現了，為什麼我們需要自組織特徵對映？原因是，除了能夠將任意維度轉換為一維或二維外，它還必須具有保留鄰域拓撲的能力。

Kohonen SOM 中的鄰域拓撲

可以有多種拓撲結構，但以下兩種拓撲結構使用得最多：

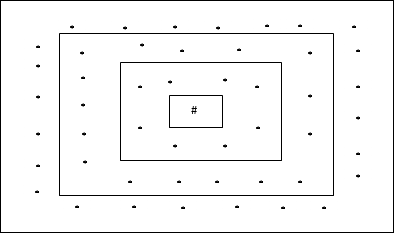
矩形網格拓撲

這種拓撲結構在距離 2 的網格中有 24 個節點，距離 1 的網格中有 16 個節點，距離 0 的網格中有 8 個節點，這意味著每個矩形網格之間的差異是 8 個節點。獲勝單元用 # 表示。

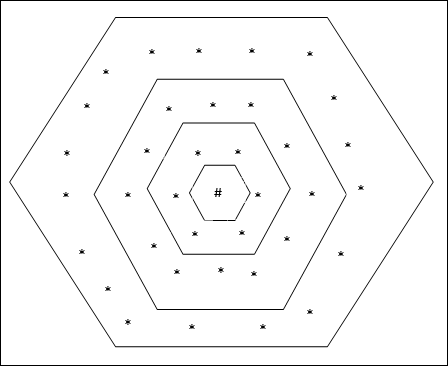
六邊形網格拓撲

這種拓撲結構在距離 2 的網格中有 18 個節點，距離 1 的網格中有 12 個節點，距離 0 的網格中有 6 個節點，這意味著每個矩形網格之間的差異是 6 個節點。獲勝單元用 # 表示。

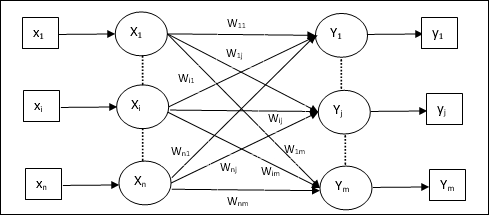
架構

KSOM 的架構類似於競爭網路。藉助前面討論的鄰域方案，可以在網路的擴充套件區域進行訓練。

訓練演算法

步驟 1 - 初始化權重、學習率 α 和鄰域拓撲方案。

步驟 2 - 當停止條件不為真時，繼續步驟 3-9。

步驟 3 - 對於每個輸入向量 x，繼續步驟 4-6。

步驟 4 - 計算 j = 1 到 m 的歐幾里得距離平方

$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n \displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$

步驟 5 - 獲取獲勝單元 J，其中 D(j) 最小。

步驟 6 - 透過以下關係計算獲勝單元的新權重：

$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha[x_{i}\:-\:w_{ij}(old)]$$

步驟 7 - 透過以下關係更新學習率 α：

$$\alpha(t\:+\:1)\:=\:0.5\alpha t$$

步驟 8 - 減小拓撲方案的半徑。

步驟 9 - 檢查網路的停止條件。