
自適應諧振理論
該網路由Stephen Grossberg和Gail Carpenter於1987年開發。它基於競爭並使用無監督學習模型。自適應諧振理論(ART)網路,顧名思義,總是開放於新的學習(自適應),而不會丟失舊的模式(諧振)。基本上,ART網路是一個向量分類器,它接受一個輸入向量並將其分類到一個類別中,這取決於它與哪個儲存模式最相似。
工作原理
ART分類的主要操作可以分為以下階段:
識別階段 - 將輸入向量與輸出層每個節點上呈現的分類進行比較。如果神經元的輸出與應用的分類最匹配,則其輸出變為“1”,否則變為“0”。
比較階段 - 在此階段,將輸入向量與比較層向量進行比較。重置的條件是相似度小於警戒引數。
搜尋階段 - 在此階段,網路將搜尋上述階段中完成的重置和匹配。因此,如果沒有重置並且匹配相當好,則分類結束。否則,將重複該過程,並且必須傳送其他儲存模式以找到正確的匹配。
ART1
這是一種ART型別,旨在對二元向量進行聚類。我們可以透過其架構來了解這一點。
ART1的架構
它包含以下兩個單元:
計算單元 - 它由以下部分組成:
輸入單元 (F1 層) - 它進一步包含以下兩個部分:
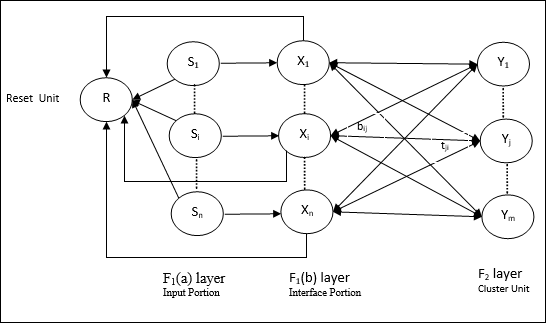
F1(a) 層 (輸入部分) - 在ART1中,除了只有輸入向量之外,此部分不會進行任何處理。它連線到F1(b)層(介面部分)。
F1(b) 層 (介面部分) - 此部分將來自輸入部分的訊號與F2層的訊號組合。F1(b)層透過自下而上的權重bij連線到F2層,F2層透過自上而下的權重tji連線到F1(b)層。
聚類單元 (F2 層) - 這是一個競爭層。選擇具有最大淨輸入的單元來學習輸入模式。所有其他聚類單元的啟用都設定為0。
重置機制 - 此機制的工作基於自上而下的權重和輸入向量之間的相似性。現在,如果這種相似度小於警戒引數,則不允許聚類學習模式,並且會發生重置。
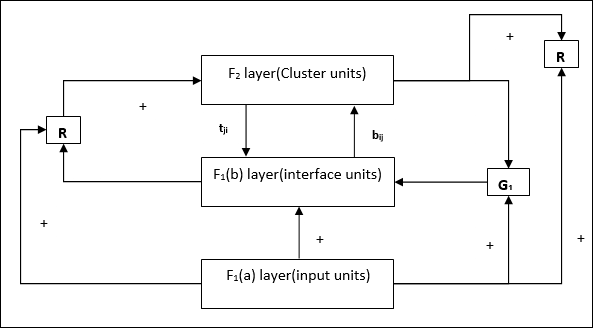
補充單元 - 實際上,重置機制的問題在於,F2層必須在某些條件下被抑制,並且在發生某些學習時也必須可用。這就是為什麼添加了兩個補充單元,即G1和G2以及重置單元R。它們被稱為增益控制單元。這些單元接收並向網路中存在的其他單元傳送訊號。“+”表示興奮性訊號,“-”表示抑制性訊號。
使用的引數
使用以下引數:
n - 輸入向量中分量的數量
m - 可以形成的叢集的最大數量
bij - 從F1(b)到F2層的權重,即自下而上的權重
tji - 從F2到F1(b)層的權重,即自上而下的權重
ρ - 警戒引數
||x|| - 向量x的範數
演算法
步驟1 - 初始化學習率、警戒引數和權重,如下所示:
$$\alpha\:>\:1\:\:and\:\:0\:<\rho\:\leq\:1$$
$$0\:<\:b_{ij}(0)\:<\:\frac{\alpha}{\alpha\:-\:1\:+\:n}\:\:and\:\:t_{ij}(0)\:=\:1$$
步驟2 - 當停止條件不為真時,繼續步驟3-9。
步驟3 - 對於每個訓練輸入,繼續步驟4-6。
步驟4 - 設定所有F1(a)和F1單元的啟用,如下所示
F2 = 0 和 F1(a) = 輸入向量
步驟5 - 將來自F1(a)到F1(b)層的輸入訊號傳送,如下所示:
$$s_{i}\:=\:x_{i}$$
步驟6 - 對於每個被抑制的F2節點
$y_{j}\:=\:\sum_i b_{ij}x_{i}$ 條件是 yj ≠ -1
步驟7 - 當重置為真時,執行步驟8-10。
步驟8 - 找到J,對於所有節點j,yJ ≥ yj
步驟9 - 再次計算F1(b)上的啟用,如下所示:
$$x_{i}\:=\:sitJi$$
步驟10 - 現在,在計算向量x和向量s的範數之後,我們需要檢查重置條件,如下所示:
如果||x||/ ||s|| < 警戒引數ρ,則抑制節點J並轉到步驟7
否則,如果||x||/ ||s|| ≥ 警戒引數ρ,則繼續。
步驟11 - 可以對節點J進行權重更新,如下所示:
$$b_{ij}(new)\:=\:\frac{\alpha x_{i}}{\alpha\:-\:1\:+\:||x||}$$
$$t_{ij}(new)\:=\:x_{i}$$
步驟12 - 必須檢查演算法的停止條件,它可能是:
- 權重沒有任何變化。
- 未對單元執行重置。
- 達到最大迭代次數。