
人工神經網路 - Hopfield 網路
Hopfield 神經網路由 John J. Hopfield 博士於 1982 年發明。它由一個包含一個或多個完全連線的迴圈神經元的單層組成。Hopfield 網路通常用於自動關聯和最佳化任務。
離散 Hopfield 網路
一種以離散方式執行的 Hopfield 網路,換句話說,可以認為輸入和輸出模式是離散向量,其本質上可以是二進位制 (0,1) 或雙極性 (+1, -1)。該網路具有對稱權重,沒有自連線,即 wij = wji 和 wii = 0。
架構
以下是一些關於離散 Hopfield 網路需要注意的重要事項:
該模型由具有一個反相輸出和一個非反相輸出的神經元組成。
每個神經元的輸出應該是其他神經元的輸入,但不能是自身的輸入。
權重/連線強度由 wij 表示。
連線可以是興奮性的,也可以是抑制性的。如果神經元的輸出與輸入相同,則為興奮性,否則為抑制性。
權重應該是對稱的,即 wij = wji
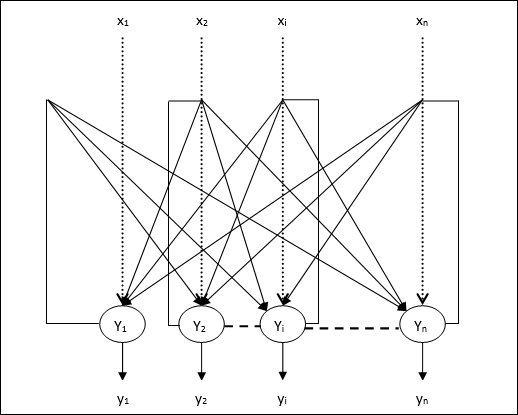
從 Y1 到 Y2、Yi 和 Yn 的輸出分別具有權重 w12、w1i 和 w1n。類似地,其他弧線在其上也有權重。
訓練演算法
在離散 Hopfield 網路的訓練過程中,權重將被更新。眾所周知,我們可以擁有二進位制輸入向量以及雙極性輸入向量。因此,在這兩種情況下,都可以使用以下關係更新權重
情況 1 - 二進位制輸入模式
對於一組二進位制模式 s(p), p = 1 到 P
這裡,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
權重矩陣由下式給出
$$w_{ij}\:=\:\sum_{p=1}^P[2s_{i}(p)-\:1][2s_{j}(p)-\:1]\:\:\:\:\:for\:i\:\neq\:j$$
情況 2 - 雙極性輸入模式
對於一組二進位制模式 s(p), p = 1 到 P
這裡,s(p) = s1(p), s2(p),..., si(p),..., sn(p)
權重矩陣由下式給出
$$w_{ij}\:=\:\sum_{p=1}^P[s_{i}(p)][s_{j}(p)]\:\:\:\:\:for\:i\:\neq\:j$$
測試演算法
步驟 1 - 初始化權重,這些權重是使用 Hebbian 原理透過訓練演算法獲得的。
步驟 2 - 如果網路的啟用未得到鞏固,則執行步驟 3-9。
步驟 3 - 對於每個輸入向量 X,執行步驟 4-8。
步驟 4 - 使網路的初始啟用等於外部輸入向量 X,如下所示:
$$y_{i}\:=\:x_{i}\:\:\:for\:i\:=\:1\:to\:n$$
步驟 5 - 對於每個單元 Yi,執行步驟 6-9。
步驟 6 - 計算網路的淨輸入,如下所示:
$$y_{ini}\:=\:x_{i}\:+\:\displaystyle\sum\limits_{j}y_{j}w_{ji}$$
步驟 7 - 對淨輸入應用以下啟用以計算輸出:
$$y_{i}\:=\begin{cases}1 & if\:y_{ini}\:>\:\theta_{i}\\y_{i} & if\:y_{ini}\:=\:\theta_{i}\\0 & if\:y_{ini}\:<\:\theta_{i}\end{cases}$$
這裡 $\theta_{i}$ 是閾值。
步驟 8 - 將此輸出 yi 廣播到所有其他單元。
步驟 9 - 測試網路的連線。
能量函式評估
能量函式定義為系統狀態的有界且非增函式。
能量函式 Ef,也稱為 Lyapunov 函式,確定離散 Hopfield 網路的穩定性,其特徵如下:
$$E_{f}\:=\:-\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^n y_{i}y_{j}w_{ij}\:-\:\displaystyle\sum\limits_{i=1}^n x_{i}y_{i}\:+\:\displaystyle\sum\limits_{i=1}^n \theta_{i}y_{i}$$
條件 - 在穩定網路中,只要節點狀態發生變化,上述能量函式就會降低。
假設當節點 i 的狀態從 $y_i^{(k)}$ 更改為 $y_i^{(k\:+\:1)}$ 時,能量變化 $\Delta E_{f}$ 由以下關係給出
$$\Delta E_{f}\:=\:E_{f}(y_i^{(k+1)})\:-\:E_{f}(y_i^{(k)})$$
$$=\:-\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{ij}y_i^{(k)}\:+\:x_{i}\:-\:\theta_{i}\end{array}\right)(y_i^{(k+1)}\:-\:y_i^{(k)})$$
$$=\:-\:(net_{i})\Delta y_{i}$$
這裡 $\Delta y_{i}\:=\:y_i^{(k\:+\:1)}\:-\:y_i^{(k)}$
能量的變化取決於一次只能更新一個單元的啟用這一事實。
連續 Hopfield 網路
與離散 Hopfield 網路相比,連續網路將時間視為連續變數。它也用於自動關聯和最佳化問題,例如旅行商問題。
模型 - 可以透過新增電子元件(例如放大器)來構建模型或架構,這些放大器可以透過 S 型啟用函式將輸入電壓對映到輸出電壓。
能量函式評估
$$E_f = \frac{1}{2}\displaystyle\sum\limits_{i=1}^n\sum_{\substack{j = 1\\ j \ne i}}^n y_i y_j w_{ij} - \displaystyle\sum\limits_{i=1}^n x_i y_i + \frac{1}{\lambda} \displaystyle\sum\limits_{i=1}^n \sum_{\substack{j = 1\\ j \ne i}}^n w_{ij} g_{ri} \int_{0}^{y_i} a^{-1}(y) dy$$
這裡 λ 是增益引數,gri 是輸入電導。