監督神經網路

上一頁
下一頁

顧名思義，監督學習是在教師的監督下進行的。這個學習過程是依賴性的。在監督學習下訓練ANN時，將輸入向量呈現給網路，網路將產生一個輸出向量。將此輸出向量與所需的/目標輸出向量進行比較。如果實際輸出與所需的/目標輸出向量之間存在差異，則會生成錯誤訊號。根據此錯誤訊號，將調整權重，直到實際輸出與所需輸出匹配。

感知器

感知器是由弗蘭克·羅森布拉特使用麥卡洛克-皮茨模型開發的，是人工神經網路的基本操作單元。它採用監督學習規則，能夠將資料分類為兩類。

感知器的操作特性：它由一個具有任意數量輸入的神經元以及可調節的權重組成，但神經元的輸出取決於閾值，為1或0。它還包括一個偏差，其權重始終為1。下圖給出了感知器的示意圖。

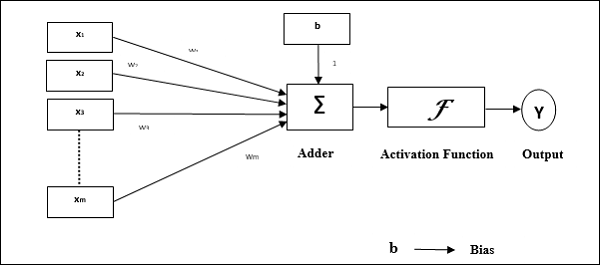
Perceptron

因此，感知器具有以下三個基本元素：

  • 連線 - 它將有一組連線連結，這些連結攜帶權重，包括一個始終權重為1的偏差。

  • 加法器 - 它在輸入乘以各自的權重後對它們進行加法。

  • 啟用函式 - 它限制神經元的輸出。最基本的啟用函式是具有兩種可能輸出的Heaviside階躍函式。如果輸入為正，則此函式返回1，對於任何負輸入則返回0。

訓練演算法

感知器網路可以針對單個輸出單元以及多個輸出單元進行訓練。

單個輸出單元的訓練演算法

步驟1 - 初始化以下內容以開始訓練：

  • 權重
  • 偏差
  • 學習率 $\alpha$

為了簡便計算和簡化，權重和偏差必須設定為0，學習率必須設定為1。

步驟2 - 當停止條件不為真時，繼續執行步驟3-8。

步驟3 - 對於每個訓練向量x，繼續執行步驟4-6。

步驟4 - 按如下方式啟用每個輸入單元：

$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$

步驟5 - 現在使用以下關係獲得淨輸入：

$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}.\:w_{i}$$

這裡'b'是偏差，'n'是輸入神經元的總數。

步驟6 - 應用以下啟用函式以獲得最終輸出。

$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{in}\:\leqslant\:\theta\\-1 & if\:y_{in}\:<\:-\theta \end{cases}$$

步驟7 - 按如下方式調整權重和偏差：

情況1 - 如果y ≠ t，則

$$w_{i}(new)\:=\:w_{i}(old)\:+\:\alpha\:tx_{i}$$

$$b(new)\:=\:b(old)\:+\:\alpha t$$

情況2 - 如果y = t，則

$$w_{i}(new)\:=\:w_{i}(old)$$

$$b(new)\:=\:b(old)$$

這裡'y'是實際輸出，'t'是所需的/目標輸出。

步驟8 - 測試停止條件，當權重沒有變化時將發生此條件。

多個輸出單元的訓練演算法

下圖是用於多個輸出類的感知器架構。

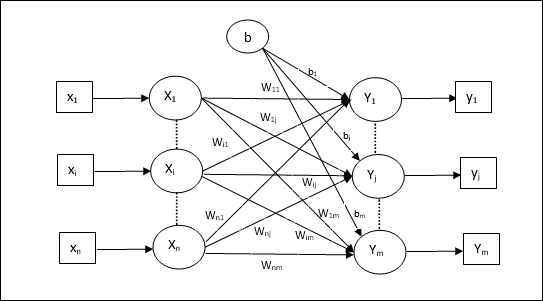
Training Algorithm

步驟1 - 初始化以下內容以開始訓練：

  • 權重
  • 偏差
  • 學習率 $\alpha$

為了簡便計算和簡化，權重和偏差必須設定為0，學習率必須設定為1。

步驟2 - 當停止條件不為真時，繼續執行步驟3-8。

步驟3 - 對於每個訓練向量x，繼續執行步驟4-6。

步驟4 - 按如下方式啟用每個輸入單元：

$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$

步驟5 - 使用以下關係獲得淨輸入：

$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}$$

這裡'b'是偏差，'n'是輸入神經元的總數。

步驟6 - 應用以下啟用函式以獲得每個輸出單元j = 1到m的最終輸出：

$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{inj}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{inj}\:\leqslant\:\theta\\-1 & if\:y_{inj}\:<\:-\theta \end{cases}$$

步驟7 - 按如下方式調整x = 1到n和j = 1到m的權重和偏差：

情況1 - 如果yj ≠ tj，則

$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha\:t_{j}x_{i}$$

$$b_{j}(new)\:=\:b_{j}(old)\:+\:\alpha t_{j}$$

情況2 - 如果yj = tj，則

$$w_{ij}(new)\:=\:w_{ij}(old)$$

$$b_{j}(new)\:=\:b_{j}(old)$$

這裡'y'是實際輸出，'t'是所需的/目標輸出。

步驟8 - 測試停止條件，當權重沒有變化時將發生此條件。

自適應線性神經元 (Adaline)

Adaline代表自適應線性神經元，是一個具有單個線性單元的網路。它由Widrow和Hoff於1960年開發。關於Adaline的一些要點如下：

  • 它使用雙極啟用函式。

  • 它使用delta規則進行訓練，以最小化實際輸出與所需/目標輸出之間的均方誤差 (MSE)。

  • 權重和偏差是可調節的。

架構

Adaline的基本結構類似於感知器，它具有一個額外的反饋迴圈，藉助該迴圈，實際輸出與所需的/目標輸出進行比較。比較後，根據訓練演算法，將更新權重和偏差。

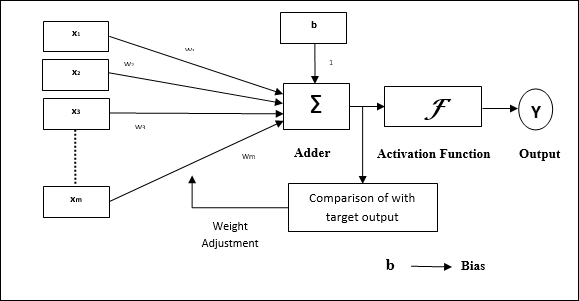
Architecture Adaptive Linear

訓練演算法

步驟1 - 初始化以下內容以開始訓練：

  • 權重
  • 偏差
  • 學習率 $\alpha$

為了簡便計算和簡化，權重和偏差必須設定為0，學習率必須設定為1。

步驟2 - 當停止條件不為真時，繼續執行步驟3-8。

步驟3 - 對於每個雙極訓練對s:t，繼續執行步驟4-6。

步驟4 - 按如下方式啟用每個輸入單元：

$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$

步驟5 - 使用以下關係獲得淨輸入：

$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{i}$$

這裡'b'是偏差，'n'是輸入神經元的總數。

步驟6 - 應用以下啟用函式以獲得最終輸出：

$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:\geqslant\:0 \\-1 & if\:y_{in}\:<\:0 \end{cases}$$

步驟7 - 按如下方式調整權重和偏差：

情況1 - 如果y ≠ t，則

$$w_{i}(new)\:=\:w_{i}(old)\:+\: \alpha(t\:-\:y_{in})x_{i}$$

$$b(new)\:=\:b(old)\:+\: \alpha(t\:-\:y_{in})$$

情況2 - 如果y = t，則

$$w_{i}(new)\:=\:w_{i}(old)$$

$$b(new)\:=\:b(old)$$

這裡'y'是實際輸出，'t'是所需的/目標輸出。

$(t\:-\;y_{in})$是計算出的誤差。

步驟8 - 測試停止條件，當權重沒有變化或訓練期間發生的最高權重變化小於指定的容差時，將發生此條件。

多自適應線性神經元 (Madaline)

Madaline代表多自適應線性神經元，是一個由許多Adaline並行組成的網路。它將有一個輸出單元。關於Madaline的一些要點如下：

  • 它就像一個多層感知器，其中Adaline充當輸入和Madaline層之間的隱藏單元。

  • 輸入和Adaline層之間的權重和偏差（如我們在Adaline架構中看到的）是可調節的。

  • Adaline和Madaline層具有固定的權重和偏差1。

  • 可以使用Delta規則進行訓練。

架構

Madaline的架構由輸入層的“n”個神經元、Adaline層的“m”個神經元和Madaline層的1個神經元組成。Adaline層可以被認為是隱藏層，因為它位於輸入層和輸出層（即Madaline層）之間。

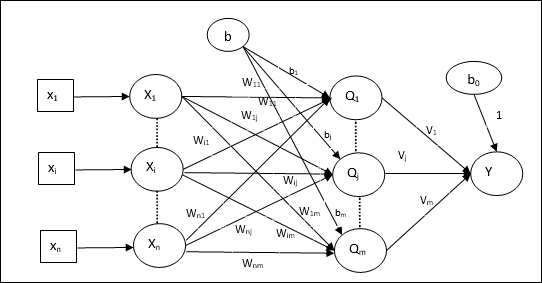
Adaline

訓練演算法

到目前為止，我們知道只有輸入和Adaline層之間的權重和偏差需要調整，而Adaline和Madaline層之間的權重和偏差是固定的。

步驟1 - 初始化以下內容以開始訓練：

  • 權重
  • 偏差
  • 學習率 $\alpha$

為了簡便計算和簡化，權重和偏差必須設定為0，學習率必須設定為1。

步驟2 - 當停止條件不為真時，繼續執行步驟3-8。

步驟3 - 對於每個雙極訓練對s:t，繼續執行步驟4-7。

步驟4 - 按如下方式啟用每個輸入單元：

$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$

步驟5 - 使用以下關係獲得每個隱藏層（即Adaline層）的淨輸入：

$$Q_{inj}\:=\:b_{j}\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}\:\:\:j\:=\:1\:to\:m$$

這裡'b'是偏差，'n'是輸入神經元的總數。

步驟6 - 應用以下啟用函式以獲得Adaline和Madaline層的最終輸出：

$$f(x)\:=\:\begin{cases}1 & if\:x\:\geqslant\:0 \\-1 & if\:x\:<\:0 \end{cases}$$

隱藏（Adaline）單元的輸出

$$Q_{j}\:=\:f(Q_{inj})$$

網路的最終輸出

$$y\:=\:f(y_{in})$$

即 $\:\:y_{inj}\:=\:b_{0}\:+\:\sum_{j = 1}^m\:Q_{j}\:v_{j}$

步驟7 - 計算誤差並調整權重如下：

情況1 - 如果y ≠ t且t = 1，則

$$w_{ij}(new)\:=\:w_{ij}(old)\:+\: \alpha(1\:-\:Q_{inj})x_{i}$$

$$b_{j}(new)\:=\:b_{j}(old)\:+\: \alpha(1\:-\:Q_{inj})$$

在這種情況下，將更新Qj上的權重，其中淨輸入接近0，因為t = 1。

情況2 - 如果y ≠ t且t = -1，則

$$w_{ik}(new)\:=\:w_{ik}(old)\:+\: \alpha(-1\:-\:Q_{ink})x_{i}$$

$$b_{k}(new)\:=\:b_{k}(old)\:+\: \alpha(-1\:-\:Q_{ink})$$

在這種情況下，將更新Qk上的權重，其中淨輸入為正，因為t = -1。

這裡'y'是實際輸出，'t'是所需的/目標輸出。

情況3 - 如果y = t，則

權重不會發生變化。

步驟8 - 測試停止條件，當權重沒有變化或訓練期間發生的最高權重變化小於指定的容差時，將發生此條件。

反向傳播神經網路

反向傳播神經網路 (BPN) 是一種多層神經網路，由輸入層、至少一個隱藏層和輸出層組成。顧名思義，此網路將進行反向傳播。透過比較目標輸出和實際輸出，在輸出層計算出的誤差將反向傳播到輸入層。

架構

如示意圖所示，BPN的架構具有三個互連層，這些層上具有權重。隱藏層和輸出層也具有偏差，其權重始終為1。從圖中可以清楚地看出，BPN的工作分為兩個階段。一個階段將訊號從輸入層傳送到輸出層，另一個階段將誤差從輸出層反向傳播到輸入層。

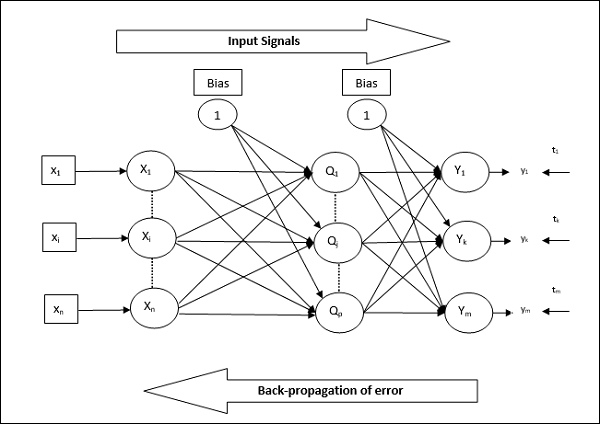
Back Propogation

訓練演算法

為了進行訓練，BPN將使用二進位制S型啟用函式。BPN的訓練將包含以下三個階段。

  • 階段1 - 前饋階段

  • 階段2 - 誤差的反向傳播

  • 階段3 - 權重的更新

所有這些步驟將在演算法中總結如下

步驟1 - 初始化以下內容以開始訓練：

  • 權重
  • 學習率 $\alpha$

為了簡便計算和簡化，請取一些小的隨機值。

步驟2 - 當停止條件不為真時，繼續執行步驟3-11。

步驟3 - 對於每個訓練對，繼續執行步驟4-10。

階段1

步驟4 - 每個輸入單元接收輸入訊號xi並將其傳送到隱藏單元，對於所有i = 1到n

步驟5 - 使用以下關係計算隱藏單元的淨輸入：

$$Q_{inj}\:=\:b_{0j}\:+\:\sum_{i=1}^n x_{i}v_{ij}\:\:\:\:j\:=\:1\:to\:p$$

這裡b0j是隱藏單元上的偏差，vij是來自輸入層i單元的隱藏層j單元上的權重。

現在透過應用以下啟用函式計算淨輸出

$$Q_{j}\:=\:f(Q_{inj})$$

將這些隱藏層單元的輸出訊號傳送到輸出層單元。

步驟6 - 使用以下關係計算輸出層單元的淨輸入：

$$y_{ink}\:=\:b_{0k}\:+\:\sum_{j = 1}^p\:Q_{j}\:w_{jk}\:\:k\:=\:1\:to\:m$$

這裡b0k⁡是輸出單元上的偏差，wjk是來自隱藏層j單元的輸出層k單元上的權重。

透過應用以下啟用函式計算淨輸出

$$y_{k}\:=\:f(y_{ink})$$

階段 2

步驟 7 − 計算誤差修正項，對應於每個輸出單元接收到的目標模式，如下所示 −

$$\delta_{k}\:=\:(t_{k}\:-\:y_{k})f^{'}(y_{ink})$$

在此基礎上，更新權重和偏差，如下所示 −

$$\Delta v_{jk}\:=\:\alpha \delta_{k}\:Q_{ij}$$

$$\Delta b_{0k}\:=\:\alpha \delta_{k}$$

然後，將 $\delta_{k}$ 反饋到隱藏層。

步驟 8 − 現在每個隱藏單元將是來自輸出單元的其增量輸入之和。

$$\delta_{inj}\:=\:\displaystyle\sum\limits_{k=1}^m \delta_{k}\:w_{jk}$$

誤差項可以計算如下 −

$$\delta_{j}\:=\:\delta_{inj}f^{'}(Q_{inj})$$

在此基礎上，更新權重和偏差，如下所示 −

$$\Delta w_{ij}\:=\:\alpha\delta_{j}x_{i}$$

$$\Delta b_{0j}\:=\:\alpha\delta_{j}$$

階段 3

步驟 9 − 每個輸出單元 (ykk = 1 到 m) 更新權重和偏差，如下所示 −

$$v_{jk}(new)\:=\:v_{jk}(old)\:+\:\Delta v_{jk}$$

$$b_{0k}(new)\:=\:b_{0k}(old)\:+\:\Delta b_{0k}$$

步驟 10 − 每個隱藏單元 (zjj = 1 到 p) 更新權重和偏差，如下所示 −

$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\Delta w_{ij}$$

$$b_{0j}(new)\:=\:b_{0j}(old)\:+\:\Delta b_{0j}$$

步驟 11 − 檢查停止條件，該條件可以是達到時期數或目標輸出與實際輸出匹配。

廣義 Delta 學習規則

Delta 規則僅適用於輸出層。另一方面，廣義 Delta 規則，也稱為反向傳播規則，是一種建立隱藏層期望值的方法。

數學公式

對於啟用函式 $y_{k}\:=\:f(y_{ink})$，隱藏層和輸出層上的淨輸入的導數可以由以下公式給出

$$y_{ink}\:=\:\displaystyle\sum\limits_i\:z_{i}w_{jk}$$

以及 $\:\:y_{inj}\:=\:\sum_i x_{i}v_{ij}$

現在需要最小化的誤差是

$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2$$

利用鏈式法則，我們有

$$\frac{\partial E}{\partial w_{jk}}\:=\:\frac{\partial }{\partial w_{jk}}(\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2)$$

$$=\:\frac{\partial }{\partial w_{jk}}\lgroup\frac{1}{2}[t_{k}\:-\:t(y_{ink})]^2\rgroup$$

$$=\:-[t_{k}\:-\:y_{k}]\frac{\partial }{\partial w_{jk}}f(y_{ink})$$

$$=\:-[t_{k}\:-\:y_{k}]f(y_{ink})\frac{\partial }{\partial w_{jk}}(y_{ink})$$

$$=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})z_{j}$$

現在假設 $\delta_{k}\:=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})$

連線到隱藏單元 zj 的權重可以由以下公式給出 −

$$\frac{\partial E}{\partial v_{ij}}\:=\:- \displaystyle\sum\limits_{k} \delta_{k}\frac{\partial }{\partial v_{ij}}\:(y_{ink})$$

代入 $y_{ink}$ 的值，我們將得到以下結果

$$\delta_{j}\:=\:-\displaystyle\sum\limits_{k}\delta_{k}w_{jk}f^{'}(z_{inj})$$

權重更新可以如下進行 −

對於輸出單元 −

$$\Delta w_{jk}\:=\:-\alpha\frac{\partial E}{\partial w_{jk}}$$

$$=\:\alpha\:\delta_{k}\:z_{j}$$

對於隱藏單元 −

$$\Delta v_{ij}\:=\:-\alpha\frac{\partial E}{\partial v_{ij}}$$

$$=\:\alpha\:\delta_{j}\:x_{i}$$

列印頁面
上一頁
下一頁
廣告

© . All rights reserved.