
人工神經網路 - 構建模組
ANN 的處理取決於以下三個構建模組:
- 網路拓撲結構
- 權重的調整或學習
- 啟用函式
在本章中,我們將詳細討論 ANN 的這三個構建模組。
網路拓撲結構
網路拓撲結構是指網路的排列方式,以及其節點和連線線。根據拓撲結構,ANN 可以分為以下幾種型別:
前饋網路
它是一個非遞迴網路,其處理單元/節點分層排列,每一層中的所有節點都與前一層的節點連線。連線具有不同的權重。沒有反饋迴路,這意味著訊號只能單向流動,從輸入到輸出。它可以分為以下兩種型別:
單層前饋網路 - 該概念是指只有一個加權層的 ANN。換句話說,我們可以說輸入層與輸出層完全連線。
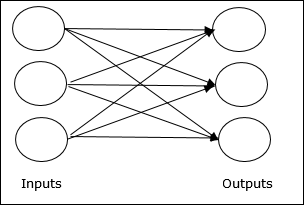
多層前饋網路 - 該概念是指具有多個加權層的 ANN。由於該網路在輸入層和輸出層之間有一個或多個層,因此稱為隱藏層。
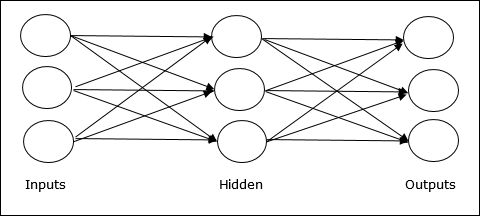
反饋網路
顧名思義,反饋網路具有反饋路徑,這意味著訊號可以透過迴路雙向流動。這使得它成為一個非線性動態系統,該系統會持續變化,直到達到平衡狀態。它可以分為以下幾種型別:
遞迴網路 - 它們是具有閉環的反饋網路。以下是兩種型別的遞迴網路。
完全遞迴網路 - 它是最簡單的 ANN 架構,因為所有節點都連線到所有其他節點,並且每個節點都充當輸入和輸出。
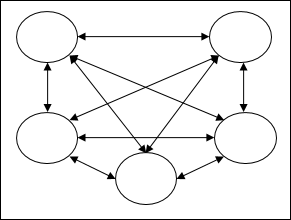
Jordan 網路 - 它是一個閉環網路,其中輸出將再次作為反饋返回到輸入,如下面的圖所示。
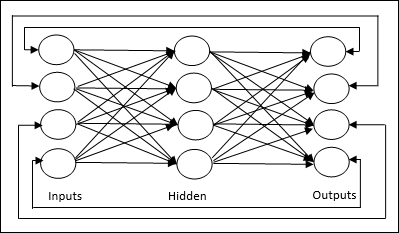
權重的調整或學習
在人工神經網路中,學習是指修改指定網路中神經元之間連線權重的方法。ANN 中的學習可以分為三類:監督學習、無監督學習和強化學習。
監督學習
顧名思義,這種型別的學習是在教師的監督下進行的。此學習過程是依賴性的。
在監督學習下訓練 ANN 期間,將輸入向量呈現給網路,網路將輸出一個輸出向量。將此輸出向量與所需的輸出向量進行比較。如果實際輸出與所需輸出向量之間存在差異,則會生成一個誤差訊號。根據此誤差訊號,調整權重,直到實際輸出與所需輸出匹配。
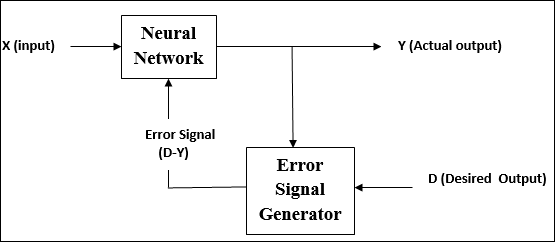
無監督學習
顧名思義,這種型別的學習是在沒有教師監督的情況下進行的。此學習過程是獨立的。
在無監督學習下訓練 ANN 期間,將相似型別的輸入向量組合成叢集。當應用新的輸入模式時,神經網路將給出輸出響應,指示輸入模式所屬的類別。
沒有來自環境的反饋,說明所需輸出是什麼以及它是否正確。因此,在這種型別的學習中,網路本身必須從輸入資料中發現模式和特徵,以及輸入資料與輸出之間的關係。
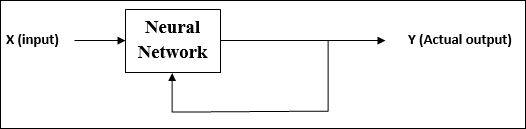
強化學習
顧名思義,這種型別的學習用於增強或加強網路對某些評論資訊。此學習過程類似於監督學習,但是我們可能的資訊非常少。
在強化學習下訓練網路期間,網路會從環境中接收一些反饋。這使得它有點類似於監督學習。但是,此處獲得的反饋是評價性的,而不是指導性的,這意味著與監督學習不同,這裡沒有教師。在接收反饋後,網路會調整權重以在將來獲得更好的評論資訊。
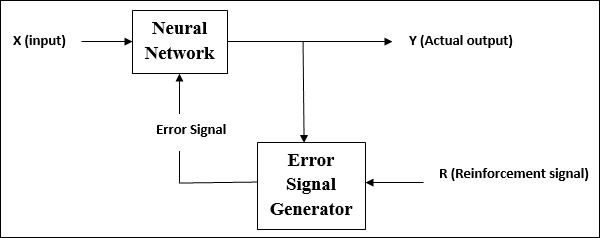
啟用函式
它可以定義為對輸入施加的額外力量或努力以獲得精確的輸出。在 ANN 中,我們還可以對輸入應用啟用函式以獲得精確的輸出。以下是我們感興趣的一些啟用函式:
線性啟用函式
它也稱為恆等函式,因為它不執行任何輸入編輯。它可以定義為:
$$F(x)\:=\:x$$
Sigmoid 啟用函式
它有兩種型別,如下所示:
二進位制 sigmoid 函式 - 此啟用函式執行 0 到 1 之間的輸入編輯。它是正向的。它始終是有界的,這意味著其輸出不能小於 0 且大於 1。它也是嚴格遞增的,這意味著輸入越多,輸出越高。它可以定義為
$$F(x)\:=\:sigm(x)\:=\:\frac{1}{1\:+\:exp(-x)}$$
雙極 sigmoid 函式 - 此啟用函式執行 -1 到 1 之間的輸入編輯。它可以是正的或負的。它始終是有界的,這意味著其輸出不能小於 -1 且大於 1。它也像 sigmoid 函式一樣嚴格遞增。它可以定義為
$$F(x)\:=\:sigm(x)\:=\:\frac{2}{1\:+\:exp(-x)}\:-\:1\:=\:\frac{1\:-\:exp(x)}{1\:+\:exp(x)}$$