時間序列 - ARIMA 的變體

在上一章中，我們已經瞭解了 ARIMA 模型的工作原理及其侷限性，即它無法處理季節性資料或多元時間序列，因此，引入了新的模型來包含這些特徵。

以下是這些新模型的簡要介紹：

向量自迴歸 (VAR)

它是多元平穩時間序列的自迴歸模型的推廣版本。其特徵在於引數 'p'。

向量移動平均 (VMA)

它是多元平穩時間序列的移動平均模型的推廣版本。其特徵在於引數 'q'。

向量自迴歸移動平均 (VARMA)

它是 VAR 和 VMA 的組合，也是多元平穩時間序列的 ARMA 模型的推廣版本。其特徵在於引數 'p' 和 'q'。就像 ARMA 透過將引數 'q' 設定為 0 可以充當 AR 模型，透過將引數 'p' 設定為 0 可以充當 MA 模型一樣，VARMA 也能夠透過將引數 'q' 設定為 0 充當 VAR 模型，透過將引數 'p' 設定為 0 充當 VMA 模型。

程式碼塊 [209]

df_multi = df[['T', 'C6H6(GT)']]
split = len(df) - int(0.2*len(df))
train_multi, test_multi = df_multi[0:split], df_multi[split:]

程式碼塊 [211]

from statsmodels.tsa.statespace.varmax import VARMAX

model = VARMAX(train_multi, order = (2,1))
model_fit = model.fit()
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, 
   due especially to identification issues. 
   EstimationWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171: 
   ValueWarning: No frequency information was provided, so inferred frequency H will be used. 
  % freq, ValueWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals 
  "Check mle_retvals", ConvergenceWarning)

程式碼塊 [213]

predictions_multi = model_fit.forecast( steps=len(test_multi))
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320: 
   FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated.  Use `pandas.date_range` instead.
   freq = base_index.freq)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues.
   EstimationWarning)

程式碼塊 [231]

plt.plot(train_multi['T'])
plt.plot(test_multi['T'])
plt.plot(predictions_multi.iloc[:,0:1], '--')
plt.show()

plt.plot(train_multi['C6H6(GT)'])
plt.plot(test_multi['C6H6(GT)'])
plt.plot(predictions_multi.iloc[:,1:2], '--')
plt.show()

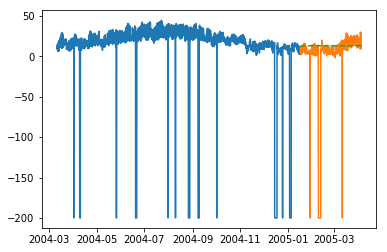
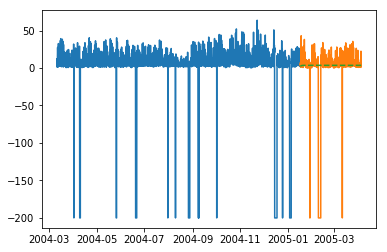
上述程式碼展示瞭如何使用 VARMA 模型對多元時間序列進行建模，儘管此模型可能並不最適合我們的資料。

帶有外生變數的 VARMA (VARMAX)

它是 VARMA 模型的擴充套件，其中使用稱為協變數的額外變數來對我們感興趣的主要變數進行建模。

季節性自迴歸積分移動平均 (SARIMA)

這是 ARIMA 模型的擴充套件，用於處理季節性資料。它將資料劃分為季節性和非季節性成分，並以類似的方式對它們進行建模。它具有 7 個引數，非季節性部分的引數 (p,d,q) 與 ARIMA 模型相同，季節性部分的引數為 (P,D,Q,m)，其中 'm' 是季節週期數，P、D、Q 與 ARIMA 模型的引數類似。這些引數可以使用網格搜尋或遺傳演算法進行校準。

帶有外生變數的 SARIMA (SARIMAX)

這是 SARIMA 模型的擴充套件，其中包含有助於我們對感興趣變數進行建模的外生變數。

在將變數作為外生變數之前，進行變數的相關性分析可能會有所幫助。

程式碼塊 [251]

from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values

corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0

皮爾遜相關係數顯示了兩個變數之間的線性關係，為了解釋結果，我們首先檢視 p 值，如果它小於 0.05，則係數的值是顯著的，否則係數的值不顯著。對於顯著的 p 值，正的相關係數值表示正相關，負的相關係數值表示負相關。

因此，對於我們的資料，“溫度”和“C6H6”似乎具有高度正相關。因此，我們將

程式碼塊 [297]

from statsmodels.tsa.statespace.sarimax import SARIMAX

model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False)
model_fit = model.fit(disp = False)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
   "Check mle_retvals", ConvergenceWarning)

程式碼塊 [298]

y_ = test_multi['C6H6(GT)'].values
predicted = model_fit.predict(exog=y_)
test_multi_ = pandas.DataFrame(test)
test_multi_['predictions'] = predicted[0:1871]

程式碼塊 [299]

plt.plot(train_multi['T'])
plt.plot(test_multi_['T'])
plt.plot(test_multi_.predictions, '--')

輸出 [299]

[<matplotlib.lines.Line2D at 0x1eab0191c18>]

與單變數 ARIMA 建模相比，這裡的預測似乎現在出現了更大的變化。

毋庸置疑的是，SARIMAX 可以透過僅將相應引數設定為非零值來用作 ARX、MAX、ARMAX 或 ARIMAX 模型。

分數自迴歸積分移動平均 (FARIMA)

有時，我們的序列可能不是平穩的，而使用引數 'd' 取值 1 進行差分可能會過度差分。因此，我們需要使用分數值對時間序列進行差分。

在資料科學領域，沒有一個最優模型，適用於您的資料的模型在很大程度上取決於您的資料集。瞭解各種模型使我們能夠選擇一個適用於我們資料的模型，並透過實驗獲得最佳結果。結果應該以圖表和誤差指標的形式呈現，有時即使是小的誤差也可能是壞的，因此，繪製和視覺化結果至關重要。

在下一章中，我們將研究另一個統計模型：指數平滑。

列印頁面