時間序列 - 快速指南

時間序列 - 簡介

時間序列是在特定時期內的一系列觀察值。單變數時間序列由單個變數在一段時間內週期性時間例項中取的值組成，而多變數時間序列由多個變數在一段時間內相同週期性時間例項中取的值組成。我們每天都會遇到的時間序列最簡單的例子是全天、一週、一個月或一年的溫度變化。

對時間資料的分析能夠讓我們對變數如何隨時間變化，或者它如何依賴於其他變數的值的變化，獲得有用的見解。可以分析變數與其先前值和/或其他變數之間的這種關係，用於時間序列預測，並在人工智慧中具有眾多應用。

時間序列 - 程式語言

對於使用者使用或開發機器學習問題，掌握任何程式語言的基本知識都是必不可少的。以下是任何想要從事機器學習工作的人員的首選程式語言列表：

Python

這是一種高階解釋型程式語言，快速且易於編碼。Python 可以遵循過程式或面向物件的程式設計範例。各種庫的存在使得實現複雜的程式更加簡單。在本教程中，我們將使用 Python 編寫程式碼，並在接下來的章節中討論對時間序列建模有用的相關庫。

R

與 Python 類似，R 是一種解釋型多正規化語言，支援統計計算和圖形處理。各種包使得在 R 中實現機器學習建模更加容易。

Java

這是一種解釋型面向物件程式語言，因其廣泛的包可用性和先進的資料視覺化技術而聞名。

C/C++

這些是編譯型語言，也是兩種最古老的程式語言。這些語言通常被用來將機器學習功能整合到現有的應用程式中，因為它們允許您輕鬆地定製機器學習演算法的實現。

MATLAB

MATrix LABoratory 是一種多正規化語言，它提供了處理矩陣的功能。它允許對複雜問題進行數學運算。它主要用於數值運算，但一些包也允許圖形化多域模擬和基於模型的設計。

其他首選用於機器學習問題的程式語言包括 JavaScript、LISP、Prolog、SQL、Scala、Julia、SAS 等。

時間序列 - Python 庫

由於其易於編寫和理解的程式碼結構以及各種開源庫，Python 在進行機器學習的個人中享有盛譽。我們在接下來的章節中將使用的一些此類開源庫已在下面介紹。

NumPy

Numerical Python 是一個用於科學計算的庫。它基於 N 維陣列物件，並提供基本數學功能，例如大小、形狀、均值、標準差、最小值、最大值，以及一些更復雜的功能，例如線性代數函式和傅立葉變換。隨著我們在這個教程中繼續學習，您將瞭解更多關於這些內容。

Pandas

這個庫提供了高效且易於使用的資料結構，例如序列、資料框和麵板。它增強了 Python 的功能，從單純的資料收集和準備到資料分析。Pandas 和 NumPy 這兩個庫使得對小型到超大型資料集的任何操作都非常簡單。要了解有關這些功能的更多資訊，請遵循本教程。

SciPy

Science Python 是一個用於科學和技術計算的庫。它提供了最佳化、訊號和影像處理、積分、插值和線性代數的功能。在執行機器學習時，這個庫非常方便。隨著我們在這個教程中繼續學習，我們將討論這些功能。

Scikit-learn

這個庫是一個 SciPy 工具包，廣泛用於統計建模、機器學習和深度學習，因為它包含各種可定製的迴歸、分類和聚類模型。它與 NumPy、Pandas 和其他庫配合良好，使其更容易使用。

Statsmodels

與 Scikit-learn 類似，這個庫用於統計資料探索和統計建模。它也與其他 Python 庫配合良好。

Matplotlib

這個庫用於以各種格式（例如線圖、條形圖、熱圖、散點圖、直方圖等）進行資料視覺化。它包含從繪圖到標籤的所有圖形相關功能。隨著我們在這個教程中繼續學習，我們將討論這些功能。

這些庫對於開始使用任何型別的資料進行機器學習非常重要。

除了上面討論的庫之外，另一個特別重要用於處理時間序列的庫是：

Datetime

這個庫及其兩個模組（datetime 和 calendar）提供了讀取、格式化和處理時間所需的所有 datetime 功能。

我們將在接下來的章節中使用這些庫。

時間序列 - 資料處理和視覺化

時間序列是在等間距時間間隔內索引的一系列觀測值。因此，在任何時間序列中都應保持順序和連續性。

我們將使用的資料集是一個多變數時間序列，包含大約一年的某個嚴重汙染的義大利城市空氣質量的小時資料。資料集可以從以下連結下載：https://archive.ics.uci.edu/ml/datasets/air+quality。

有必要確保：

時間序列是等間距的，並且
其中沒有冗餘值或缺口。

如果時間序列不連續，我們可以對其進行上取樣或下采樣。

顯示 df.head()

In [122]

import pandas

In [123]

df = pandas.read_csv("AirQualityUCI.csv", sep = ";", decimal = ",")
df = df.iloc[ : , 0:14]

In [124]

len(df)

Out[124]

In [125]

df.head()

Out[125]

為了預處理時間序列，我們確保資料集中沒有 NaN（NULL）值；如果有，我們可以將它們替換為 0 或平均值或前一個或後一個值。替換比刪除更可取，這樣可以保持時間序列的連續性。但是，在我們的資料集中，最後幾個值似乎是 NULL，因此刪除不會影響連續性。

刪除 NaN（非數字）

In [126]

df.isna().sum()
Out[126]:
Date             114
Time             114
CO(GT)           114
PT08.S1(CO)      114
NMHC(GT)         114
C6H6(GT)         114
PT08.S2(NMHC)    114
NOx(GT)          114
PT08.S3(NOx)     114
NO2(GT)          114
PT08.S4(NO2)     114
PT08.S5(O3)      114
T                114
RH               114
dtype: int64

In [127]

df = df[df['Date'].notnull()]

In [128]

df.isna().sum()

Out[128]

Date             0
Time             0
CO(GT)           0
PT08.S1(CO)      0
NMHC(GT)         0
C6H6(GT)         0
PT08.S2(NMHC)    0
NOx(GT)          0
PT08.S3(NOx)     0
NO2(GT)          0
PT08.S4(NO2)     0
PT08.S5(O3)      0
T                0
RH               0
dtype: int64

時間序列通常以線圖的形式相對於時間繪製。為此，我們現在將合併日期和時間列，並將其從字串轉換為 datetime 物件。這可以使用 datetime 庫來完成。

轉換為 datetime 物件

In [129]

df['DateTime'] = (df.Date) + ' ' + (df.Time)
print (type(df.DateTime[0]))

<class 'str'>

In [130]

import datetime

df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))
print (type(df.DateTime[0]))

讓我們看看一些變數（如溫度）如何隨著時間的變化而變化。

顯示圖表

In [131]

df.index = df.DateTime

In [132]

import matplotlib.pyplot as plt
plt.plot(df['T'])

Out[132]

[<matplotlib.lines.Line2D at 0x1eaad67f780>]

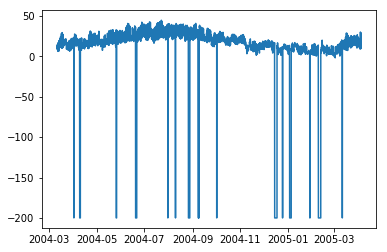
In [208]

plt.plot(df['C6H6(GT)'])

Out[208]

[<matplotlib.lines.Line2D at 0x1eaaeedff28>]

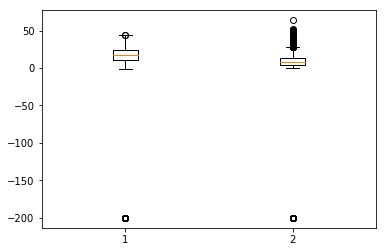
箱線圖是另一種有用的圖表型別，它允許您將大量有關資料集的資訊壓縮到單個圖表中。它顯示了一個或多個變數的均值、25% 和 75% 分位數以及異常值。當異常值數量很少且與均值相距甚遠時，我們可以透過將異常值設定為均值或 75% 分位數值來消除異常值。

顯示箱線圖

In [134]

plt.boxplot(df[['T','C6H6(GT)']].values)

Out[134]

{'whiskers': [<matplotlib.lines.Line2D at 0x1eaac16de80>,
   <matplotlib.lines.Line2D at 0x1eaac16d908>,
   <matplotlib.lines.Line2D at 0x1eaac177a58>,
   <matplotlib.lines.Line2D at 0x1eaac177cf8>],
   'caps': [<matplotlib.lines.Line2D at 0x1eaac16d2b0>,
   <matplotlib.lines.Line2D at 0x1eaac16d588>,
   <matplotlib.lines.Line2D at 0x1eaac1a69e8>,
   <matplotlib.lines.Line2D at 0x1eaac1a64a8>],
   'boxes': [<matplotlib.lines.Line2D at 0x1eaac16dc50>,
   <matplotlib.lines.Line2D at 0x1eaac1779b0>],
   'medians': [<matplotlib.lines.Line2D at 0x1eaac16d4a8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c50>],
   'fliers': [<matplotlib.lines.Line2D at 0x1eaac177dd8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c18>],'means': []
}

時間序列 - 建模

簡介

時間序列具有以下四個組成部分：

水平 - 它是級數變化的平均值。
趨勢 - 它是變數隨時間增加或減少的行為。
季節性 - 它是時間序列的週期性行為。
噪聲 - 這是由於環境因素而新增到觀測值中的誤差。

時間序列建模技術

為了捕捉這些組成部分，有很多流行的時間序列建模技術。本節簡要介紹了每種技術，但是我們將在接下來的章節中詳細討論它們：

樸素方法

這些是簡單的估計技術，例如，預測值等於時間相關變數的前一個值的均值或前一個實際值。這些用於與複雜的建模技術進行比較。

自迴歸

自迴歸將未來時間段的值預測為先前時間段的值的函式。自迴歸的預測可能比樸素方法更能擬合數據，但它可能無法解釋季節性。

ARIMA 模型

自迴歸積分移動平均模型將變數的值建模為平穩時間序列先前值的線性函式和先前時間步長的殘差誤差。然而，現實世界的資料可能是非平穩的並且具有季節性，因此開發了季節性 ARIMA 和分數 ARIMA。ARIMA 用於單變數時間序列，為了處理多個變數，引入了 VARIMA。

指數平滑

它將變數的值建模為先前值的指數加權線性函式。該統計模型也可以處理趨勢和季節性。

LSTM

長短期記憶模型 (LSTM) 是一種迴圈神經網路，用於時間序列以解釋長期依賴關係。它可以用大量資料進行訓練以捕獲多變數時間序列中的趨勢。

上述建模技術用於時間序列迴歸。在接下來的章節中，讓我們逐一探索所有這些。

時間序列 - 引數校準

簡介

任何統計或機器學習模型都有一些引數，這些引數極大地影響了資料的建模方式。例如，ARIMA 具有 p、d、q 值。這些引數的確定應使實際值與建模值之間的誤差最小。引數校準可以說是模型擬閤中最關鍵和最耗時的任務。因此，為我們選擇最佳引數非常重要。

引數校準方法

有多種方法可以校準引數。本節將詳細介紹其中一些方法。

反覆試驗

一種常見的模型校準方法是手動校準，您從視覺化時間序列開始，直觀地嘗試一些引數值，並反覆更改它們，直到達到足夠好的擬合度。這需要對我們正在嘗試的模型有很好的理解。對於 ARIMA 模型，手動校準是藉助自相關圖來確定“p”引數，偏自相關圖來確定“q”引數，ADF 檢驗來確認時間序列的平穩性並設定“d”引數來完成的。我們將在接下來的章節中詳細討論所有這些。

網格搜尋

另一種模型校準方法是網格搜尋，這實質上意味著您嘗試為所有可能的引數組合構建模型，並選擇誤差最小的模型。這很耗時，因此當要校準的引數數量和它們取值的範圍較少時很有用，因為這涉及多個巢狀的 for 迴圈。

遺傳演算法

遺傳演算法基於生物學原理，即好的解決方案最終會進化到最“優”的解決方案。它使用生物學中的突變、交叉和選擇操作最終達到最優解。

要了解更多知識，您可以閱讀其他引數最佳化技術，例如貝葉斯最佳化和群體智慧最佳化。

時間序列 - 樸素方法

簡介

樸素方法，例如假設t時刻的預測值等於t-1時刻變數的實際值，或使用序列的移動平均值，用於衡量統計模型和機器學習模型的效能，並強調它們的必要性。

在本章中，讓我們嘗試將這些模型應用於時間序列資料的一個特徵。

首先，我們將檢視資料中“溫度”特徵的均值及其周圍的偏差。檢視最高和最低溫度值也很有用。這裡可以使用numpy庫的功能。

顯示統計資料

In [135]

import numpy
print (
   'Mean: ',numpy.mean(df['T']), '; 
   Standard Deviation: ',numpy.std(df['T']),'; 
   \nMaximum Temperature: ',max(df['T']),'; 
   Minimum Temperature: ',min(df['T'])
)

我們獲得了9357個觀測值在等間隔時間線上的統計資料，這些資料有助於我們理解資料。

現在我們將嘗試第一種樸素方法，將當前時刻的預測值設定為前一時刻的實際值，並計算其均方根誤差 (RMSE) 以量化該方法的效能。

顯示第一種樸素方法

In [136]

df['T']
df['T_t-1'] = df['T'].shift(1)

In [137]

df_naive = df[['T','T_t-1']][1:]

In [138]

from sklearn import metrics
from math import sqrt

true = df_naive['T']
prediction = df_naive['T_t-1']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 1: ', error)

樸素方法 1 的 RMSE：12.901140576492974

讓我們看看下一個樸素方法，其中當前時刻的預測值等於其之前時間段的平均值。我們也將計算此方法的RMSE。

顯示第二種樸素方法

In [139]

df['T_rm'] = df['T'].rolling(3).mean().shift(1)
df_naive = df[['T','T_rm']].dropna()

In [140]

true = df_naive['T']
prediction = df_naive['T_rm']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 2: ', error)

樸素方法 2 的 RMSE：14.957633272839242

在這裡，您可以嘗試不同的先前時間段數，也稱為“滯後”，這裡設定為3。在這個資料集中可以看出，隨著滯後數量的增加，誤差也會增加。如果滯後設定為1，它就與之前使用的樸素方法相同。

注意事項

您可以編寫一個非常簡單的函式來計算均方根誤差。這裡，我們使用了'sklearn'包中的均方誤差函式，然後取其平方根。
在pandas中，df['column_name']也可以寫成df.column_name，但是對於這個資料集，df.T與df['T']的作用不同，因為df.T是轉置資料框的函式。因此，只使用df['T']或考慮在使用其他語法之前重新命名此列。

時間序列 - 自迴歸

對於平穩時間序列，自迴歸模型將t時刻變數的值視為其前p個時間步長的值的線性函式。數學上可以寫成：

$$y_{t} = \:C+\:\phi_{1}y_{t-1}\:+\:\phi_{2}Y_{t-2}+...+\phi_{p}y_{t-p}+\epsilon_{t}$$

其中，‘p’是自迴歸趨勢引數

$\epsilon_{t}$是白噪聲，並且

$y_{t-1}, y_{t-2}\:\: ...y_{t-p}$表示變數在先前時間段的值。

p的值可以使用各種方法進行校準。找到合適的'p'值的一種方法是繪製自相關圖。

注意 - 在對資料進行任何分析之前，我們應該將資料按照8:2的比例分成訓練集和測試集，因為測試資料僅用於找出模型的準確性，並且假設在我們做出預測之後才能獲得測試資料。在時間序列的情況下，資料點的順序非常重要，因此在分割資料時應注意不要丟失順序。

自相關圖或相關圖顯示了變數與其自身在先前時間步長的關係。它利用皮爾遜相關係數，並顯示95%置信區間內的相關性。讓我們看看它在我們的資料“溫度”變數中的樣子。

顯示自相關圖

In [141]

split = len(df) - int(0.2*len(df))
train, test = df['T'][0:split], df['T'][split:]

In [142]

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(train, lags = 100)
plt.show()

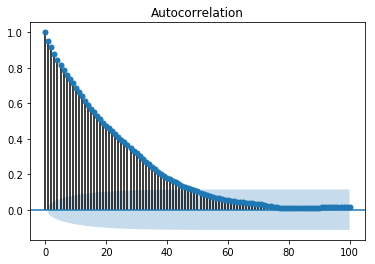
所有位於藍色陰影區域之外的滯後值都被認為具有相關性。

時間序列 - 移動平均

對於平穩時間序列，移動平均模型將t時刻變數的值視為其前q個時間步長的殘差誤差的線性函式。殘差誤差是透過將t時刻的值與之前值的移動平均值進行比較來計算的。

數學上可以寫成：

$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$

其中‘q’是移動平均趨勢引數

$\epsilon_{t}$是白噪聲，並且

$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$是先前時間段的誤差項。

可以使用各種方法校準'q'的值。找到合適的'q'值的一種方法是繪製偏自相關圖。

偏自相關圖顯示了變數與其自身在先前時間步長的關係，消除了間接相關性，這與顯示直接和間接相關性的自相關圖不同，讓我們看看它在我們的資料“溫度”變數中的樣子。

顯示偏自相關圖

In [143]

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(train, lags = 100)
plt.show()

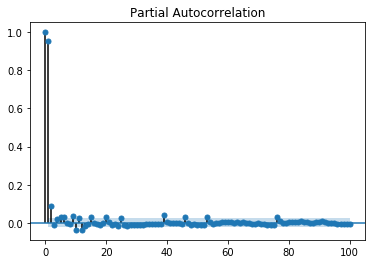
偏自相關圖的解讀方式與相關圖相同。

時間序列 - ARIMA

我們已經瞭解到，對於平穩時間序列，t時刻的變數是先前觀測值或殘差誤差的線性函式。因此，現在是時候將兩者結合起來，形成自迴歸移動平均 (ARMA) 模型了。

然而，有時時間序列不是平穩的，即序列的統計特性（如均值、方差）會隨時間變化。而我們迄今為止研究的統計模型都假設時間序列是平穩的，因此，我們可以加入一個對時間序列進行差分以使其平穩的預處理步驟。現在，重要的是我們要找出我們正在處理的時間序列是否平穩。

查詢時間序列平穩性的各種方法包括：觀察時間序列圖中的季節性或趨勢，檢查不同時間段的均值和方差差異，增廣迪基-福勒 (ADF) 檢驗，KPSS 檢驗，赫斯特指數等。

讓我們使用 ADF 檢驗看看我們資料集的“溫度”變數是否是平穩時間序列。

In [74]

from statsmodels.tsa.stattools import adfuller

result = adfuller(train)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value In result[4].items()
   print('\t%s: %.3f' % (key, value))

ADF 統計量：-10.406056

p 值：0.000000

臨界值

1%: -3.431

5%: -2.862

10%: -2.567

既然我們已經運行了 ADF 檢驗，讓我們解釋一下結果。首先，我們將 ADF 統計量與臨界值進行比較，較低的臨界值告訴我們該序列很可能是非平穩的。接下來，我們檢視 p 值。p 值大於 0.05 也表明時間序列是非平穩的。

或者，p 值小於或等於 0.05，或 ADF 統計量小於臨界值，表明時間序列是平穩的。

因此，我們正在處理的時間序列已經是平穩的了。對於平穩時間序列，我們將'd'引數設定為0。

我們也可以使用赫斯特指數來確認時間序列的平穩性。

In [75]

import hurst

H, c,data = hurst.compute_Hc(train)
print("H = {:.4f}, c = {:.4f}".format(H,c))

H = 0.1660，c = 5.0740

H<0.5 表示反永續性行為，H>0.5 表示永續性行為或趨勢序列。H=0.5 表示隨機遊走/布朗運動。H<0.5 的值證實了我們的序列是平穩的。

對於非平穩時間序列，我們將'd'引數設定為1。此外，自迴歸趨勢引數'p'和移動平均趨勢引數'q'是在平穩時間序列上計算的，即透過對時間序列進行差分後繪製自相關圖和偏自相關圖來計算。

ARIMA 模型由三個引數 (p,d,q) 構成，現在我們已經清楚了，所以讓我們對我們的時間序列進行建模並預測未來的溫度值。

In [156]

from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(train.values, order=(5, 0, 2))
model_fit = model.fit(disp=False)

In [157]

predictions = model_fit.predict(len(test))
test_ = pandas.DataFrame(test)
test_['predictions'] = predictions[0:1871]

In [158]

plt.plot(df['T'])
plt.plot(test_.predictions)
plt.show()

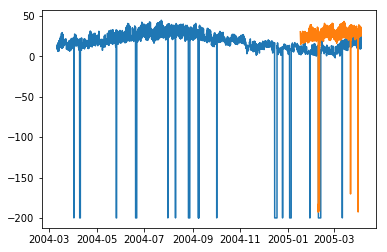
In [167]

error = sqrt(metrics.mean_squared_error(test.values,predictions[0:1871]))
print ('Test RMSE for ARIMA: ', error)

ARIMA 模型的測試 RMSE：43.21252940234892

時間序列 - ARIMA 的變體

在上一章中，我們已經瞭解了 ARIMA 模型的工作原理及其侷限性，即它無法處理季節性資料或多元時間序列，因此，引入了新的模型來包含這些特徵。

這裡簡要介紹一下這些新模型：

向量自迴歸 (VAR)

它是多元平穩時間序列的自迴歸模型的推廣版本。它由'p'引數構成。

向量移動平均 (VMA)

它是多元平穩時間序列的移動平均模型的推廣版本。它由'q'引數構成。

向量自迴歸移動平均 (VARMA)

它是 VAR 和 VMA 的組合，也是多元平穩時間序列的 ARMA 模型的推廣版本。它由'p'和'q'引數構成。就像 ARMA 可以透過將'q'引數設定為0來充當 AR 模型，透過將'p'引數設定為0來充當 MA 模型一樣，VARMA 也能夠透過將'q'引數設定為0來充當 VAR 模型，透過將'p'引數設定為0來充當 VMA 模型。

In [209]

df_multi = df[['T', 'C6H6(GT)']]
split = len(df) - int(0.2*len(df))
train_multi, test_multi = df_multi[0:split], df_multi[split:]

In [211]

from statsmodels.tsa.statespace.varmax import VARMAX

model = VARMAX(train_multi, order = (2,1))
model_fit = model.fit()
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, 
   due especially to identification issues. 
   EstimationWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171: 
   ValueWarning: No frequency information was provided, so inferred frequency H will be used. 
  % freq, ValueWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals 
  "Check mle_retvals", ConvergenceWarning)

In [213]

predictions_multi = model_fit.forecast( steps=len(test_multi))
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320: 
   FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated.  Use `pandas.date_range` instead.
   freq = base_index.freq)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues.
   EstimationWarning)

In [231]

plt.plot(train_multi['T'])
plt.plot(test_multi['T'])
plt.plot(predictions_multi.iloc[:,0:1], '--')
plt.show()

plt.plot(train_multi['C6H6(GT)'])
plt.plot(test_multi['C6H6(GT)'])
plt.plot(predictions_multi.iloc[:,1:2], '--')
plt.show()

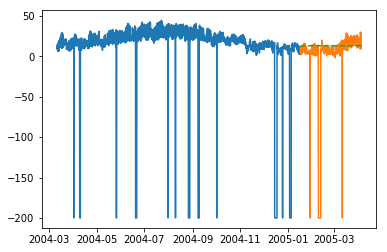
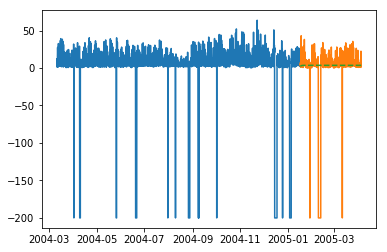
上述程式碼顯示瞭如何使用 VARMA 模型對多元時間序列進行建模，儘管該模型可能不適合我們的資料。

具有外生變數的 VARMA (VARMAX)

它是 VARMA 模型的擴充套件，其中使用稱為協變數的額外變數來模擬我們感興趣的主要變數。

季節性自迴歸積分移動平均 (SARIMA)

這是 ARIMA 模型的擴充套件，用於處理季節性資料。它將資料分為季節性和非季節性成分，並以類似的方式對它們進行建模。它由7個引數構成，非季節性部分 (p,d,q) 引數與 ARIMA 模型相同，季節性部分 (P,D,Q,m) 引數中'm'是季節週期數，P,D,Q與 ARIMA 模型的引數類似。這些引數可以使用網格搜尋或遺傳演算法進行校準。

具有外生變數的 SARIMA (SARIMAX)

這是 SARIMA 模型的擴充套件，其中包含有助於我們對感興趣的變數進行建模的外生變數。

在將變數作為外生變數輸入之前，進行變數的相關性分析可能會有用。

In [251]

from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values

corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0

皮爾遜相關係數顯示了兩個變數之間的線性關係，為了解釋結果，我們首先檢視 p 值，如果它小於 0.05，則係數的值是顯著的，否則係數的值是不顯著的。對於顯著的 p 值，正的相關係數值表示正相關，負的值表示負相關。

因此，對於我們的資料，“溫度”和“C6H6”似乎具有高度的正相關性。因此，我們將

In [297]

from statsmodels.tsa.statespace.sarimax import SARIMAX

model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False)
model_fit = model.fit(disp = False)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
   "Check mle_retvals", ConvergenceWarning)

In [298]

y_ = test_multi['C6H6(GT)'].values
predicted = model_fit.predict(exog=y_)
test_multi_ = pandas.DataFrame(test)
test_multi_['predictions'] = predicted[0:1871]

In [299]

plt.plot(train_multi['T'])
plt.plot(test_multi_['T'])
plt.plot(test_multi_.predictions, '--')

Out[299]

[<matplotlib.lines.Line2D at 0x1eab0191c18>]

與單變數 ARIMA 建模相比，這裡的預測現在似乎有更大的變化。

不用說，SARIMAX 可以透過將相應的引數設定為非零值來用作 ARX、MAX、ARMAX 或 ARIMAX 模型。

分數自迴歸積分移動平均模型 (FARIMA)

有時，我們的序列可能不是平穩的，但使用引數‘d’取值為1進行差分可能會過度差分。因此，我們需要使用分數值對時間序列進行差分。

在資料科學領域，沒有一個最優模型，哪個模型適合你的資料很大程度上取決於你的資料集。瞭解各種模型使我們能夠選擇一個適用於我們資料的模型，並透過試驗該模型來獲得最佳結果。結果應該以圖表和誤差指標的形式呈現，有時即使是很小的誤差也可能是壞的，因此，繪製和視覺化結果至關重要。

在下一章中，我們將研究另一個統計模型：指數平滑。

時間序列 - 指數平滑

在本章中，我們將討論時間序列指數平滑涉及的技術。

簡單指數平滑

指數平滑是一種透過對一段時間內的資料賦予指數遞減的權重來平滑單變數時間序列的技術。

數學上，給定時間t的值，時間‘t+1’時變數的值 y_(t+1|t) 定義為：

$$y_{t+1|t}\:=\:\alpha y_{t}\:+\:\alpha\lgroup1 -\alpha\rgroup y_{t-1}\:+\alpha\lgroup1-\alpha\rgroup^{2}\:y_{t-2}\:+\:...+y_{1}$$

其中，$0\leq\alpha \leq1$ 是平滑引數，並且

$y_{1},....,y_{t}$ 是網路流量在時間1、2、3、……、t之前的數值。

這是一種對沒有明顯趨勢或季節性的時間序列進行建模的簡單方法。但是指數平滑也可以用於具有趨勢和季節性的時間序列。

三重指數平滑

三重指數平滑 (TES) 或 Holt-Winters 方法，將指數平滑應用三次——水平平滑 $l_{t}$、趨勢平滑 $b_{t}$ 和季節性平滑 $S_{t}$，其中 $\alpha$、$\beta^{*}$ 和 $\gamma$ 為平滑引數，‘m’為季節性頻率，即一年中的季節數。

根據季節性成分的性質，TES 有兩類：

Holt-Winters 加法模型——當季節性是加法性質時。
Holt-Winters 乘法模型——當季節性是乘法性質時。

對於非季節性時間序列，我們只有趨勢平滑和水平平滑，這被稱為 Holt 的線性趨勢法。

讓我們嘗試將三重指數平滑應用於我們的資料。

程式碼塊 [316]

from statsmodels.tsa.holtwinters import ExponentialSmoothing

model = ExponentialSmoothing(train.values, trend= )
model_fit = model.fit()

程式碼塊 [322]

predictions_ = model_fit.predict(len(test))

程式碼塊 [325]

plt.plot(test.values)
plt.plot(predictions_[1:1871])

輸出 [325]

[<matplotlib.lines.Line2D at 0x1eab00f1cf8>]

在這裡，我們已經使用訓練集訓練過一次模型，然後我們繼續進行預測。更現實的方法是在一個或多個時間步長後重新訓練模型。當我們從訓練資料（直到時間‘t’）中獲得時間‘t+1’的預測值時，下一個時間‘t+2’的預測可以使用直到時間‘t+1’的訓練資料進行，因為此時‘t+1’的實際值將已知。這種對一個或多個未來步驟進行預測然後重新訓練模型的方法稱為滾動預測或前滾驗證。

時間序列 - 前向驗證

在時間序列建模中，隨著時間的推移，預測變得越來越不準確，因此，隨著實際資料的可用性，使用實際資料重新訓練模型以進行進一步預測是一種更現實的方法。由於統計模型的訓練不耗時，因此前滾驗證是獲得最準確結果的首選解決方案。

讓我們對我們的資料應用一步前滾驗證，並將其與我們之前獲得的結果進行比較。

程式碼塊 [333]

prediction = []
data = train.values
for t In test.values:
   model = (ExponentialSmoothing(data).fit())
   y = model.predict()
   prediction.append(y[0])
   data = numpy.append(data, t)

程式碼塊 [335]

test_ = pandas.DataFrame(test)
test_['predictionswf'] = prediction

程式碼塊 [341]

plt.plot(test_['T'])
plt.plot(test_.predictionswf, '--')
plt.show()

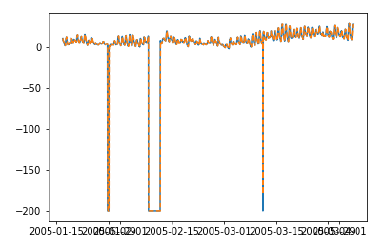
程式碼塊 [340]

error = sqrt(metrics.mean_squared_error(test.values,prediction))
print ('Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation: ', error)
Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation:  11.787532205759442

我們可以看到，我們的模型現在效能明顯更好。事實上，趨勢跟蹤得如此緊密，以至於在圖中預測值與實際值重疊。你也可以嘗試將前滾驗證應用於 ARIMA 模型。

時間序列 - Prophet 模型

2017年，Facebook 開源了 Prophet 模型，該模型能夠對具有強多重季節性（日級、周級、年級等）和趨勢的時間序列進行建模。它具有直觀的引數，即使不是專家級別的資料科學家也可以調整這些引數以獲得更好的預測結果。其核心是一個加性迴歸模型，可以檢測變化點以對時間序列進行建模。

Prophet 將時間序列分解成趨勢 $g_{t}$、季節性 $S_{t}$ 和節假日 $h_{t}$ 的組成部分。

$$y_{t}=g_{t}+s_{t}+h_{t}+\epsilon_{t}$$

其中，$\epsilon_{t}$ 是誤差項。

谷歌和推特分別在 R 中引入了類似的時間序列預測包，例如因果影響和異常檢測。

時間序列 - LSTM 模型

現在，我們已經熟悉了時間序列的統計建模，但是機器學習現在非常流行，因此熟悉一些機器學習模型也很重要。我們將從時間序列領域最流行的模型開始——長短期記憶模型。

LSTM 是一種迴圈神經網路。所以在我們學習 LSTM 之前，瞭解神經網路和迴圈神經網路是必要的。

神經網路

人工神經網路是由相互連線的神經元組成的分層結構，其靈感來自於生物神經網路。它不是一種演算法，而是各種演算法的組合，使我們能夠對資料進行復雜的操作。

迴圈神經網路

它是一種專門處理時間序列資料的神經網路。RNN 的神經元具有單元狀態/記憶，輸入根據這種內部狀態進行處理，這是透過神經網路中的迴圈實現的。RNN 中有重複的“tanh”層模組，允許它們保留資訊。然而，不能長期保留，這就是我們需要 LSTM 模型的原因。

LSTM

它是一種特殊的迴圈神經網路，能夠學習資料中的長期依賴關係。這是因為模型的重複模組包含四個相互作用的層。

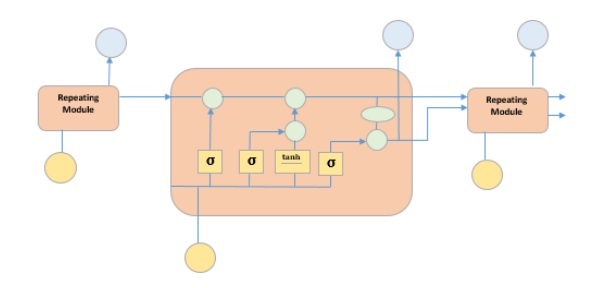
上圖描繪了黃框中的四個神經網路層，綠圈中的逐點運算子，黃圈中的輸入和藍圈中的單元狀態。LSTM 模組具有單元狀態和三個門，這使它們能夠選擇性地學習、遺忘或保留來自每個單元的資訊。LSTM 中的單元狀態透過只允許少量線性互動來幫助資訊在單元之間流動而不會被改變。每個單元都有一個輸入門、輸出門和一個遺忘門，它們可以向單元狀態新增或刪除資訊。遺忘門決定應該忘記來自先前單元狀態的哪些資訊，為此它使用 sigmoid 函式。輸入門使用“sigmoid”和“tanh”的逐點乘法運算分別控制資訊流向當前單元狀態。最後，輸出門決定應該將哪些資訊傳遞給下一個隱藏狀態。

現在我們已經瞭解了 LSTM 模型的內部工作原理，讓我們來實現它。為了理解 LSTM 的實現，我們將從一個簡單的例子開始——一條直線。讓我們看看 LSTM 是否能夠學習直線的規律並對其進行預測。

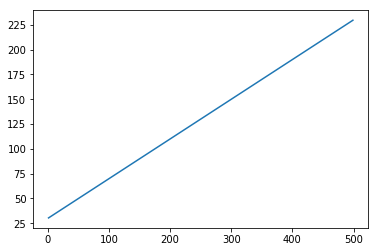
首先讓我們建立一個描繪直線的資料集。

程式碼塊 [402]

x = numpy.arange (1,500,1)
y = 0.4 * x + 30
plt.plot(x,y)

輸出 [402]

[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]

程式碼塊 [403]

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

現在資料已經建立並被分成訓練集和測試集。讓我們根據回溯期的值將時間序列資料轉換為監督學習資料的形式，這實際上是預測時間‘t’的值所看到的滯後數量。

因此，像這樣的時間序列：

time variable_x
t1  x1
t2  x2
 :   :
 :   :
T   xT

當回溯期為 1 時，將轉換為：

x1   x2
x2   x3
 :    :
 :    :
xT-1 xT

程式碼塊 [404]

def create_dataset(n_X, look_back):
   dataX, dataY = [], []
   for i in range(len(n_X)-look_back):
      a = n_X[i:(i+look_back), ]
      dataX.append(a)
      dataY.append(n_X[i + look_back, ])
   return numpy.array(dataX), numpy.array(dataY)

程式碼塊 [405]

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)

trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

現在我們將訓練我們的模型。

將少量訓練資料批次顯示給網路，當整個訓練資料以批次形式顯示給模型並計算誤差時的一次執行稱為一個 epoch。 epochs 需要執行直到誤差減少。

程式碼塊 []

from keras.models import Sequential
from keras.layers import LSTM, Dense

model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')

程式碼塊 [407]

model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)

現在讓我們看看我們的預測結果如何。

程式碼塊 [408]

plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

輸出 [408]

[<matplotlib.lines.Line2D at 0x1eac792f048>]

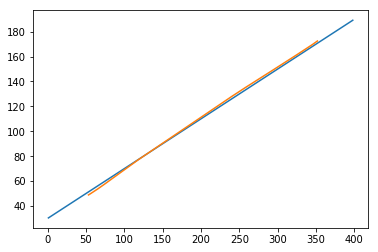
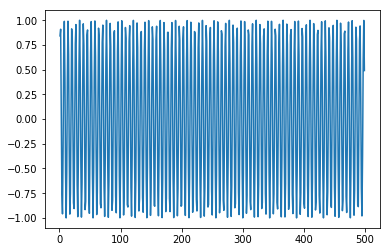
現在，我們應該嘗試以類似的方式對正弦或餘弦波進行建模。您可以執行下面給出的程式碼並修改模型引數以檢視結果如何變化。

程式碼塊 [409]

x = numpy.arange (1,500,1)
y = numpy.sin(x)
plt.plot(x,y)

輸出 [409]

[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]

程式碼塊 [410]

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

程式碼塊 [411]

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)
trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

程式碼塊 []

model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')

程式碼塊 [413]

model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)

程式碼塊 [415]

plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

輸出 [415]

[<matplotlib.lines.Line2D at 0x1eac7a1f550>]

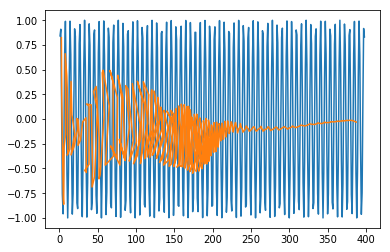
現在您可以開始處理任何資料集了。

時間序列 - 誤差指標

量化模型的效能以將其用作反饋和比較非常重要。在本教程中，我們使用了最流行的誤差指標之一：均方根誤差。還有其他各種可用的誤差指標。本章簡要討論了這些指標。

均方誤差

它是預測值和真實值之間差值的平方平均值。Sklearn 提供它作為函式。它具有與真實值和預測值的平方相同的單位，並且始終為正。

$$MSE = \frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}\:-y_{t}\rgroup^{2}$$

其中 $y'_{t}$ 是預測值，

$y_{t}$ 是實際值，並且

n 是測試集中值的總數。

從方程中可以清楚地看出，MSE 對較大的誤差或異常值懲罰更大。

均方根誤差

它是均方誤差的平方根。它也始終為正，並且在資料的範圍內。

$$RMSE = \sqrt{\frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}-y_{t}\rgroup ^2}$$

其中，$y'_{t}$ 是預測值

$y_{t}$ 是實際值，並且

n 是測試集中值的總數。

它是一次方的，因此與 MSE 相比更易於解釋。RMSE 對較大誤差的懲罰也更大。我們在教程中使用了 RMSE 指標。

平均絕對誤差

它是預測值和真實值之間絕對差值的平均值。它與預測值和真實值的單位相同，並且始終為正。

$$MAE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^{t=n} | y'{t}-y_{t}\lvert$$

其中，$y'_{t}$ 是預測值，

$y_{t}$ 是實際值，並且

n 是測試集中值的總數。

平均百分比誤差

它是預測值和真實值之間絕對差值的平均值百分比，除以真實值。

$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{y'_{t}-y_{t}}{y_{t}}*100\: \%$$

其中，$y'_{t}$ 是預測值，

$y_{t}$ 是實際值，n 是測試集中值的總數。

但是，使用此誤差的缺點是正誤差和負誤差可以相互抵消。因此，使用平均絕對百分比誤差。

平均絕對百分比誤差

它是預測值和真實值之間絕對差值的平均值百分比，除以真實值。

$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{|y'_{t}-y_{t}\lvert}{y_{t}}*100\: \%$$

其中 $y'_{t}$ 是預測值

$y_{t}$ 是實際值，並且

n 是測試集中值的總數。

時間序列 - 應用

在本教程中，我們討論了時間序列分析，這使我們瞭解到時間序列模型首先從現有的觀測中識別趨勢和季節性，然後根據這種趨勢和季節性預測值。這種分析在各個領域都很有用，例如：

財務分析——包括銷售預測、庫存分析、股票市場分析、價格估算。
天氣分析——包括溫度估算、氣候變化、季節性變化識別、天氣預報。
網路資料分析——包括網路使用預測、異常或入侵檢測、預測性維護。
醫療保健分析——包括人口普查預測、保險福利預測、病人監控。

時間序列 - 進一步研究

機器學習處理各種型別的問題。事實上，幾乎所有領域都有可能借助機器學習實現自動化或改進。下面列出了一些正在進行大量工作的此類問題。

時間序列資料

這是根據時間變化的資料，因此時間在其中起著至關重要的作用，我們在本教程中對此進行了廣泛的討論。

非時間序列資料

它是不依賴於時間的資料，大部分機器學習問題都集中在非時間序列資料上。為簡單起見，我們將對其進行進一步分類：

數值資料 − 與人類不同，計算機只理解數字，因此所有型別的資料最終都會被轉換為數值資料用於機器學習，例如，影像資料被轉換為 (r,b,g) 值，字元被轉換為 ASCII 碼或單詞被索引為數字，語音資料被轉換為包含數值資料的 mfcc 檔案。
影像資料 − 計算機視覺徹底改變了計算機的世界，它在醫學、衛星成像等領域有著廣泛的應用。
文字資料 − 自然語言處理 (NLP) 用於文字分類、釋義檢測和語言摘要。這就是讓谷歌和Facebook變得智慧的原因。
語音資料 − 語音處理涉及語音識別和情感理解。它在賦予計算機類人品質方面發揮著至關重要的作用。

列印頁面