時間序列 - ARIMA

我們已經瞭解到，對於平穩的時間序列，時間為 't' 的變數是先前觀測值或殘差誤差的線性函式。因此，現在是時候將兩者結合起來，形成一個自迴歸移動平均 (ARMA) 模型。

然而，有時時間序列不是平穩的，即序列的統計特性（如均值、方差）會隨時間變化。而我們迄今為止研究過的統計模型都假設時間序列是平穩的，因此，我們可以加入一個時間序列差分的前處理步驟來使其平穩。現在，我們需要弄清楚我們正在處理的時間序列是否平穩。

查詢時間序列平穩性的各種方法包括：檢視時間序列圖中的季節性或趨勢、檢查不同時間段的均值和方差差異、增強 Dickey-Fuller (ADF) 檢驗、KPSS 檢驗、Hurst 指數等。

讓我們使用 ADF 檢驗看看我們資料集中的“溫度”變數是否是平穩的時間序列。

In [74]

from statsmodels.tsa.stattools import adfuller

result = adfuller(train)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value In result[4].items()
   print('\t%s: %.3f' % (key, value))

ADF 統計量：-10.406056

p 值：0.000000

臨界值

1%: -3.431

5%: -2.862

10%: -2.567

現在我們已經運行了 ADF 檢驗，讓我們來解讀結果。首先，我們將 ADF 統計量與臨界值進行比較，較低的臨界值告訴我們該序列很可能是非平穩的。接下來，我們檢視 p 值。p 值大於 0.05 也表明時間序列是非平穩的。

或者，p 值小於或等於 0.05，或 ADF 統計量小於臨界值表明時間序列是平穩的。

因此，我們正在處理的時間序列已經是平穩的。對於平穩的時間序列，我們將 'd' 引數設定為 0。

我們也可以使用 Hurst 指數確認時間序列的平穩性。

In [75]

import hurst

H, c,data = hurst.compute_Hc(train)
print("H = {:.4f}, c = {:.4f}".format(H,c))

H = 0.1660，c = 5.0740

H<0.5 的值表示反永續性行為，H>0.5 表示永續性行為或趨勢序列。H=0.5 表示隨機遊走/布朗運動。H<0.5 的值證實了我們的序列是平穩的。

對於非平穩的時間序列，我們將 'd' 引數設定為 1。此外，自迴歸趨勢引數 'p' 和移動平均趨勢引數 'q' 的值是在平穩的時間序列上計算的，即透過在時間序列差分後繪製 ACP 和 PACP 來計算。

ARIMA 模型由 3 個引數 (p、d、q) 構成，現在對我們來說已經清楚了，所以讓我們對我們的時間序列進行建模並預測未來溫度值。

In [156]

from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(train.values, order=(5, 0, 2))
model_fit = model.fit(disp=False)

In [157]

predictions = model_fit.predict(len(test))
test_ = pandas.DataFrame(test)
test_['predictions'] = predictions[0:1871]

In [158]

plt.plot(df['T'])
plt.plot(test_.predictions)
plt.show()

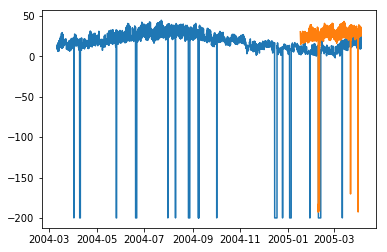
In [167]

error = sqrt(metrics.mean_squared_error(test.values,predictions[0:1871]))
print ('Test RMSE for ARIMA: ', error)

ARIMA 的測試 RMSE：43.21252940234892

列印頁面