時間序列 - 自迴歸

對於平穩時間序列，自迴歸模型將時間 't' 處的變數值視為其之前 'p' 個時間步長的值的線性函式。數學上可以寫成 -

$$y_{t} = \:C+\:\phi_{1}y_{t-1}\:+\:\phi_{2}Y_{t-2}+...+\phi_{p}y_{t-p}+\epsilon_{t}$$

其中，‘p’ 是自迴歸趨勢引數

$\epsilon_{t}$ 是白噪聲，並且

$y_{t-1}, y_{t-2}\:\: ...y_{t-p}$ 表示變數在先前時間段的值。

可以使用各種方法校準 p 的值。找到 'p' 的合適值的一種方法是繪製自相關圖。

注意 - 在對資料進行任何分析之前，我們應該將資料以 8:2 的比例分成訓練集和測試集，因為測試資料僅用於找出模型的準確性，並且假設是，在進行預測之前，我們無法獲得它。在時間序列的情況下，資料點的順序非常重要，因此在分割資料時應注意不要丟失順序。

自相關圖或相關圖顯示了變數與其自身在先前時間步長的關係。它利用皮爾遜相關係數，並在 95% 的置信區間內顯示相關性。讓我們看看它在我們資料的“溫度”變數中是什麼樣的。

顯示 ACP

在 [141]

split = len(df) - int(0.2*len(df))
train, test = df['T'][0:split], df['T'][split:]

在 [142]

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(train, lags = 100)
plt.show()

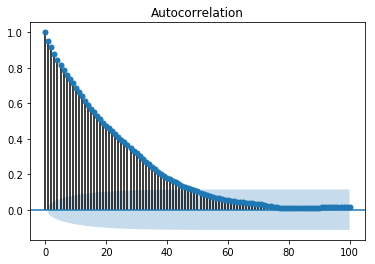
所有位於陰影藍色區域之外的滯後值都被認為具有相關性。