
時間序列 - LSTM 模型
現在,我們已經熟悉了時間序列上的統計建模,但是機器學習現在非常流行,因此熟悉一些機器學習模型也是必不可少的。我們將從時間序列領域最流行的模型開始——長短期記憶模型。
LSTM 是一種迴圈神經網路。所以在我們學習 LSTM 之前,必須先了解神經網路和迴圈神經網路。
神經網路
人工神經網路是由相互連線的神經元組成的分層結構,其靈感來自於生物神經網路。它不是一種演算法,而是各種演算法的組合,使我們能夠對資料進行復雜的運算。
迴圈神經網路
它是一類專門處理時間序列資料的神經網路。RNN 的神經元具有單元狀態/記憶,輸入根據這種內部狀態進行處理,這是透過神經網路中的迴圈實現的。RNN 中有重複的“tanh”層模組,使它們能夠保留資訊。然而,並不能長期保留,這就是為什麼我們需要 LSTM 模型。
LSTM
它是一種特殊的迴圈神經網路,能夠學習資料中的長期依賴關係。這是因為模型的迴圈模組包含四個相互作用的層。
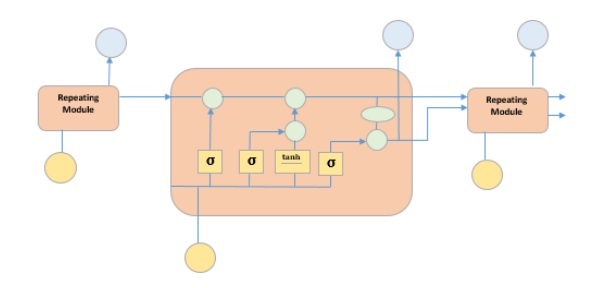
上圖描繪了四個用黃色方框表示的神經網路層,綠色圓圈表示逐點運算子,黃色圓圈表示輸入,藍色圓圈表示單元狀態。LSTM 模組具有單元狀態和三個門,這使它們能夠選擇性地學習、遺忘或保留來自每個單元的資訊。LSTM 中的單元狀態透過僅允許少量線性互動來幫助資訊在單元之間流動而不會被改變。每個單元都有一個輸入門、輸出門和一個遺忘門,可以向單元狀態新增或刪除資訊。遺忘門決定應忘記來自先前單元狀態的哪些資訊,為此它使用 sigmoid 函式。輸入門使用“sigmoid”和“tanh”的逐點乘法運算來控制資訊流向當前單元狀態。最後,輸出門決定應將哪些資訊傳遞到下一個隱藏狀態。
現在我們已經瞭解了 LSTM 模型的內部工作原理,讓我們來實現它。為了理解 LSTM 的實現,我們將從一個簡單的例子開始——一條直線。讓我們看看 LSTM 是否能夠學習直線的關係並進行預測。
首先,讓我們建立一個描述直線的資料集。
程式碼塊 [402]
x = numpy.arange (1,500,1) y = 0.4 * x + 30 plt.plot(x,y)
輸出 [402]
[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]
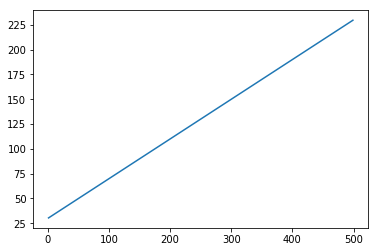
程式碼塊 [403]
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):] trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):] train = numpy.array(list(zip(trainx,trainy))) test = numpy.array(list(zip(trainx,trainy)))
現在資料已經建立並分成訓練集和測試集。讓我們根據回溯期的值將時間序列資料轉換為監督學習資料的形式,回溯期實質上是預測時間“t”處值的滯後數量。
因此,這樣的時間序列:
time variable_x t1 x1 t2 x2 : : : : T xT
當回溯期為 1 時,轉換為:
x1 x2 x2 x3 : : : : xT-1 xT
程式碼塊 [404]
def create_dataset(n_X, look_back):
dataX, dataY = [], []
for i in range(len(n_X)-look_back):
a = n_X[i:(i+look_back), ]
dataX.append(a)
dataY.append(n_X[i + look_back, ])
return numpy.array(dataX), numpy.array(dataY)
程式碼塊 [405]
look_back = 1 trainx,trainy = create_dataset(train, look_back) testx,testy = create_dataset(test, look_back) trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2)) testx = numpy.reshape(testx, (testx.shape[0], 1, 2))
現在我們將訓練我們的模型。
將少量訓練資料展示給網路,當整個訓練資料以批次的形式展示給模型並計算誤差時的一次執行稱為一個 epoch。epoch 需要執行到誤差減少為止。
程式碼塊 []
from keras.models import Sequential
from keras.layers import LSTM, Dense
model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')
程式碼塊 [407]
model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)
現在讓我們看看我們的預測結果。
程式碼塊 [408]
plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2]) plt.plot(predict[:,0:1], predict[:,1:2])
輸出 [408]
[<matplotlib.lines.Line2D at 0x1eac792f048>]
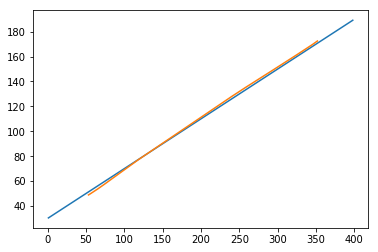
現在,我們應該嘗試以類似的方式對正弦波或餘弦波進行建模。您可以執行下面給出的程式碼並調整模型引數以檢視結果如何變化。
程式碼塊 [409]
x = numpy.arange (1,500,1) y = numpy.sin(x) plt.plot(x,y)
輸出 [409]
[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]
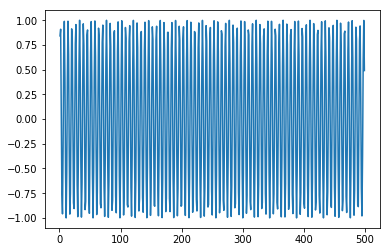
程式碼塊 [410]
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):] trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):] train = numpy.array(list(zip(trainx,trainy))) test = numpy.array(list(zip(trainx,trainy)))
程式碼塊 [411]
look_back = 1 trainx,trainy = create_dataset(train, look_back) testx,testy = create_dataset(test, look_back) trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2)) testx = numpy.reshape(testx, (testx.shape[0], 1, 2))
程式碼塊 []
model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')
程式碼塊 [413]
model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)
程式碼塊 [415]
plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2]) plt.plot(predict[:,0:1], predict[:,1:2])
輸出 [415]
[<matplotlib.lines.Line2D at 0x1eac7a1f550>]
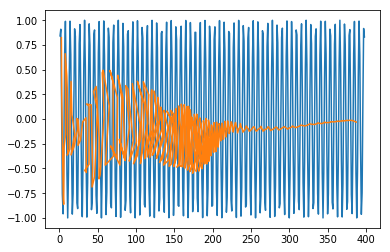
現在您可以開始處理任何資料集了。