時間序列 - 移動平均

對於平穩時間序列，移動平均模型將時間 't' 處的變數值視為前 'q' 個時間步長的殘差誤差的線性函式。透過比較時間 't' 處的值和之前值的移動平均值來計算殘差誤差。

在數學上可以寫成 -

$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$

其中'q' 是移動平均趨勢引數

$\epsilon_{t}$ 是白噪聲，並且

$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$ 是前一時期的誤差項。

可以使用多種方法來校準 'q' 的值。一種尋找合適的 'q' 值的方法是繪製偏自相關圖。

偏自相關圖顯示變數與其自身在早期時間步長處的關係，移除了間接相關性，這與自相關圖不同，自相關圖顯示直接相關性和間接相關性，讓我們看看對於我們資料的 'temperature' 變數它看起來如何。

顯示 PACP

In [143]

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(train, lags = 100)
plt.show()

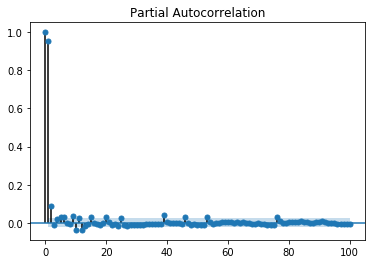
偏自相關與相關圖以相同的方式進行讀取。