雷達系統 - 快速指南

---

---

雷達系統 - 概述

雷達是一種基於電磁波的探測系統，它透過輻射電磁波並研究回波或反射波來工作。

雷達的全稱是無線電探測和測距。探測是指目標是否存在。目標可以是靜止的或移動的，即非靜止的。測距是指雷達和目標之間的距離。

雷達可用於地面、海上和太空的各種應用。雷達的應用列在下面。

• 控制空中交通
• 船舶安全
• 探測偏遠地區
• 軍事應用

在任何雷達應用中，基本原理都相同。現在讓我們討論雷達的原理。

雷達基本原理

雷達用於探測物體並確定其位置。我們可以從下圖瞭解雷達的基本原理。

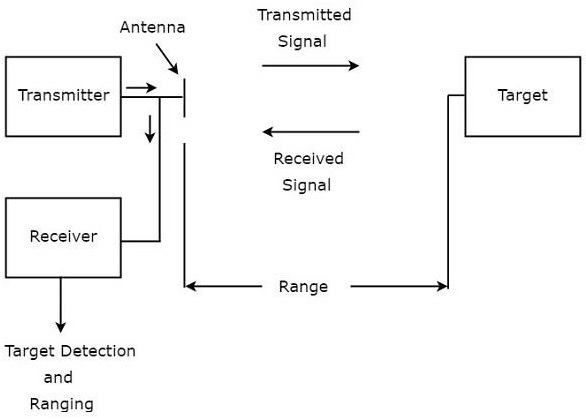
如圖所示，雷達主要由發射機和接收機組成。它使用相同的射頻天線進行訊號發射和接收。發射機的功能是將雷達訊號傳輸到目標方向。

目標將接收到的訊號反射到各個方向。反射回天線的訊號被接收機接收。

雷達系統術語

以下是本教程中一些有用的基本術語。

• 距離
• 脈衝重複頻率
• 最大無模糊距離
• 最小距離

現在，讓我們逐一討論這些基本術語。

距離

雷達與目標之間的距離稱為目標的距離或簡稱為距離 R。我們知道雷達向目標發射訊號，目標相應地以光速 C 向雷達傳送回波訊號。

設訊號從雷達傳播到目標再返回雷達所需的時間為“T”。雷達和目標之間的雙程距離將是 2R，因為雷達和目標之間的距離是 R。

現在，速度的公式如下。

$$速度= \frac{距離}{時間}$$

$$\Rightarrow 距離=速度\times 時間$$

$$\Rightarrow 2R=C\times T$$

$$R=\frac{CT}{2}\:\:\:\:\:公式\:1$$

透過在公式 1 中代入 C 和 T 的值，我們可以找到目標的距離。

脈衝重複頻率

雷達訊號應在每個時鐘脈衝處發射。兩個時鐘脈衝之間的持續時間應正確選擇，以便在下一個時鐘脈衝之前接收對應於當前時鐘脈衝的回波訊號。典型的雷達波形如下圖所示。

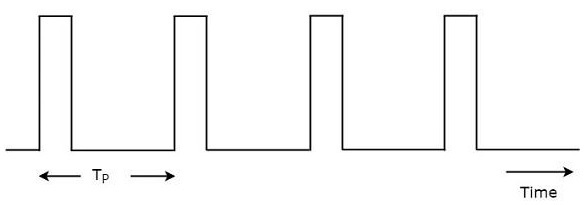
如圖所示，雷達發射週期性訊號。它具有一系列窄矩形脈衝。連續時鐘脈衝之間的時間間隔稱為脈衝重複時間，$T_P$。

脈衝重複時間的倒數稱為脈衝重複頻率，$f_P$。數學上，它可以表示為

$$f_P=\frac{1}{T_P}\:\:\:\:\:公式\:2$$

因此，脈衝重複頻率就是雷達發射訊號的頻率。

最大無模糊距離

我們知道雷達訊號應在每個時鐘脈衝處發射。如果我們選擇兩個時鐘脈衝之間的較短持續時間，則對應於當前時鐘脈衝的回波訊號將在下一個時鐘脈衝之後接收。由於此原因，目標的距離似乎小於實際距離。

因此，我們必須選擇兩個時鐘脈衝之間的持續時間，以便在下一個時鐘脈衝開始之前接收對應於當前時鐘脈衝的回波訊號。然後，我們將獲得目標的真實距離，它也稱為目標的最大無模糊距離或簡稱為最大無模糊距離。

在公式 1 中代入 $R=R_{un}$ 和 $T=T_P$。

$$R_{un}=\frac{CT_P}{2}\:\:\:\:\:公式\:3$$

從公式 2，我們將得到脈衝重複時間 $T_P$ 為脈衝重複頻率 $f_P$ 的倒數。數學上，它可以表示為

$$T_P=\frac{1}{f_P}\:\:\:\:\:公式\:4$$

將公式 4 代入公式 3。

$$R_{un}=\frac{C\left ( \frac{1}{f_P} \right )}{2}$$

$$R_{un}=\frac{C}{2f_P}\:\:\:\:\:公式\:5$$

我們可以使用公式 3 或公式 5 來計算目標的最大無模糊距離。

• 透過在公式 3 中代入 C 和 $T_P$ 的值，我們將得到目標的最大無模糊距離 $R_{un}$ 的值。

• 類似地，透過在公式 5 中代入 C 和 $f_P$ 的值，我們將得到目標的最大無模糊距離 $R_{un}$ 的值。

最小距離

當我們將訊號從雷達發射後回波訊號到達雷達所需的時間考慮為脈衝寬度時，我們將得到目標的最小距離。它也稱為目標的最短距離。

在公式 1 中代入 $R=R_{min}$ 和 $T=\tau$。

$$R_{min}=\frac{C\tau}{2}\:\:\:\:\:公式\:6$$

透過在公式 6 中代入 C 和 $\tau$ 的值，我們將得到目標的最小距離 $R_{min}$ 的值。

雷達系統 - 測距方程

雷達測距方程可用於從理論上瞭解目標的距離。在本章中，我們將討論雷達測距方程的標準形式，然後討論雷達測距方程的兩種修正形式。

我們將從雷達測距方程的標準形式得到雷達測距方程的這些修正形式。現在，讓我們討論雷達測距方程標準形式的推導。

雷達測距方程的推導

雷達測距方程的標準形式也稱為雷達測距方程的簡單形式。現在，讓我們推匯出雷達測距方程的標準形式。

我們知道功率密度就是功率與面積之比。因此，距離雷達 R 處的功率密度 $P_{di}$ 可以用數學表示為：

$$P_{di}=\frac{P_t}{4\pi R^2}\:\:\:\:\:公式\:1$$

其中，

$P_t$ 是雷達發射機發射的功率量

上述功率密度對於各向同性天線是有效的。通常，雷達使用定向天線。因此，定向天線引起的功率密度 $P_{dd}$ 將為：

$$P_{dd}=\frac{P_tG}{4\pi R^2}\:\:\:\:\:公式\:2$$

目標從接收到的輸入功率向不同方向輻射功率。反射回雷達的功率量取決於其橫截面。因此，回波訊號在雷達處的功率密度 $P_{de}$ 可以用數學表示為：

$$P_{de}=P_{dd}\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:公式\:3$$ 將公式 2 代入公式 3。

$$P_{de}=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:公式\:4$$

雷達接收的功率 $P_r$ 取決於接收天線的有效孔徑 $A_e$。

$$P_r=P_{de}A_e\:\:\:\:\:公式\:5$$

將公式 4 代入公式 5。

$$P_r=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )A_e$$

$$\Rightarrow P_r=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 R^4}$$

$$\Rightarrow R^4=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}$$

$$\Rightarrow R=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}\right ]^{1/4}\:\:\:\:\:公式\:6$$

雷達測距方程的標準形式

如果回波訊號的功率小於最小可檢測訊號的功率，則雷達無法檢測到目標，因為它超出了雷達範圍的最大限度。

因此，當接收到的回波訊號的功率等於最小可檢測訊號的功率時，可以說目標的距離為最大距離。透過在公式 6 中代入 $R=R_{Max}$ 和 $P_r=S_{min}$，我們將得到以下方程。

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:公式\:7$$

公式 7 表示雷達測距方程的標準形式。使用上述方程，我們可以找到目標的最大距離。

雷達測距方程的修正形式

我們知道定向天線的增益 G 和有效孔徑 $A_e$ 之間存在以下關係。

$$G=\frac{4\pi A_e}{\lambda^2}\:\:\:\:\:公式\:8$$

將公式 8 代入公式 7。

$$R_{Max}=\left [ \frac{P_t\sigma A_e}{\left ( 4\pi \right )^2S_{min}}\left ( \frac{4\pi A_e}{\lambda^2} \right ) \right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}\:\:\:\:\:公式\:9$$

公式 9 表示雷達測距方程的修正形式。使用上述方程，我們可以找到目標的最大距離。

我們將從公式 8 得到有效孔徑 $A_e$ 和定向天線的增益 G 之間的以下關係。

$$A_e=\frac{G\lambda^2}{4\pi}\:\:\:\:\:公式\:10$$

將公式 10 代入公式 7。

$$R_{Max}=\left [\frac{P_tG\sigma}{\left (4\pi\right )^2 S_{min}}(\frac{G\lambda^2}{4\pi})\right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG^2 \lambda^2 \sigma}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:公式\:11$$

公式 11 表示雷達測距方程的另一種修正形式。使用上述方程，我們可以找到目標的最大距離。

注意 - 基於給定的資料，我們可以使用以下三個方程之一來找到目標的最大距離：

• 公式 7
• 公式 9
• 公式 11

例題

在前一部分，我們得到了雷達距離方程的標準形式和修正形式。現在，讓我們用這些方程來解決幾個問題。

問題 1

計算以下規格的雷達最大探測距離：

• 雷達發射峰值功率，$P_t=250KW$
• 發射天線增益，$G=4000$
• 接收天線的有效孔徑，$A_e=4\:m^2$
• 目標的雷達截面，$\sigma=25\:m^2$
• 最小可檢測訊號功率，$S_{min}=10^{-12}W$

解答

為了計算給定規格下的雷達最大探測距離，我們可以使用雷達距離方程的以下標準形式。

$$R_{Max}=\left [\frac{P_tG \sigma A_e}{\left (4\pi \right )^2 S_{min}}\right ]^{1/4}$$

將所有給定的引數代入上述方程。

$$R_{Max}=\left [\frac{ \left ( 250\times 10^3 \right )\left ( 4000 \right )\left ( 25 \right )\left ( 4 \right )}{\left ( 4\pi \right )^2 \left ( 10^{-12} \right )} \right ]^{1/4}$$

$$\Rightarrow R_{Max}=158\:KM$$

因此，給定規格下的雷達最大探測距離為$158\:KM$。

問題 2

計算以下規格的雷達最大探測距離。

• 工作頻率，$f=10GHZ$
• 雷達發射峰值功率，$P_t=400KW$
• 接收天線的有效孔徑，$A_e=5\:m^2$
• 目標的雷達截面，$\sigma=30\:m^2$
• 最小可檢測訊號功率，$S_{min}=10^{-10}W$

解答

我們知道根據工作頻率f，工作波長$\lambda$的公式如下。

$$\lambda =\frac{C}{f}$$

將$C=3\times 10^8m/sec$和$f=10GHZ$代入上述方程。

$$\lambda =\frac{3\times 10^8}{10\times 10^9}$$

$$\Rightarrow \lambda=0.03m$$

所以，當工作頻率$f$為$10GHZ$時，工作波長$\lambda$等於$0.03m$。

為了計算給定規格下的雷達最大探測距離，我們可以使用雷達距離方程的以下修正形式。

$$R_{Max}=\left [\frac{P_t \sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}$$

將給定引數代入上述方程。

$$R_{Max}=\left [ \frac{\left ( 400\times 10^3 \right )\left ( 30 \right )\left ( 5^2 \right )}{4\pi\left ( 0.003 \right )^2\left ( 10 \right )^{-10}} \right ]^{1/4}$$

$$\Rightarrow R_{Max}=128KM$$

因此，給定規格下的雷達最大探測距離為$128\:KM$。

雷達系統 - 效能因素

影響雷達效能的因素被稱為雷達效能因素。本章，我們將討論這些因素。我們知道雷達距離方程的以下標準形式，它可用於計算給定規格下的雷達最大探測距離。

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

其中，

$P_t$是雷達發射的峰值功率

$G$是發射天線的增益

$\sigma$是目標的雷達截面

$A_e$是接收天線的有效孔徑

$S_{min}$是最小可檢測訊號的功率

從上述方程，我們可以得出結論，為了使雷達的探測距離最大化，應考慮以下條件。

• 雷達發射的峰值功率$P_t$應很高。
• 發射天線的增益$G$應很高。
• 目標的雷達截面$\sigma$應很高。
• 接收天線的有效孔徑$A_e$應很高。
• 最小可檢測訊號功率$S_{min}$應很低。

很難根據雷達距離方程的標準形式來預測目標的距離。這意味著雷達距離方程關於目標距離的精度較低。因為目標的雷達截面$\sigma$和最小可檢測訊號$S_{min}$具有統計特性。

最小可檢測訊號

如果回波訊號具有最小功率，雷達檢測到該訊號被稱為最小可檢測訊號。這意味著，如果訊號功率小於最小功率，雷達無法檢測到回波訊號。

通常，雷達除了接收噪聲外還會接收回波訊號。如果使用閾值來檢測接收訊號中目標的存在，則這種檢測稱為閾值檢測。

我們必須根據待檢測訊號的強度選擇合適的閾值。

• 當待檢測訊號強度高時，應選擇較高的閾值，以便消除其中存在的不需要的噪聲訊號。

• 類似地，當待檢測訊號強度低時，應選擇較低的閾值。

下圖說明了這個概念：

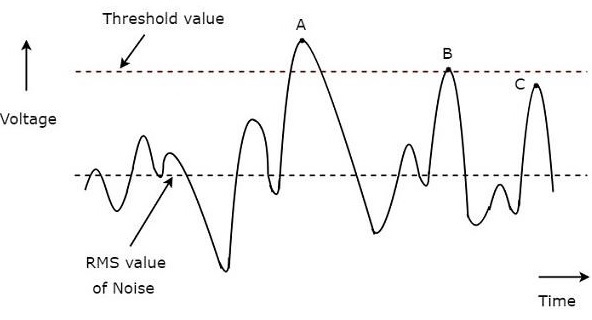
上圖顯示了雷達接收機的典型波形。x軸和y軸分別表示時間和電壓。圖中用虛線表示噪聲的有效值和閾值。

在上圖中，我們考慮了三個點A、B和C，用於識別有效檢測和漏檢。

• A點的訊號值大於閾值。因此，這是一個有效檢測。

• B點的訊號值等於閾值。因此，這是一個有效檢測。

• 即使C點的訊號值接近閾值，它也是一個漏檢。因為C點的訊號值小於閾值。

因此，A點和B點是有效檢測。而C點是漏檢。

接收機噪聲

如果接收機將噪聲分量引入到接收機接收的訊號中，則這種噪聲稱為接收機噪聲。接收機噪聲是不需要的分量；我們應該嘗試透過一些預防措施來消除它。

然而，存在一種被稱為熱噪聲的噪聲。它是由傳導電子的熱運動引起的。數學上，我們可以將接收機產生的熱噪聲功率$N_i$寫成：

$$N_i=KT_oB_n$$

其中，

$K$是玻爾茲曼常數，等於$1.38\times 10^{-23}J/deg$

$T_o$是絕對溫度，等於$290^0K$

$B_n$是接收機頻寬

品質因數

品質因數F不過是輸入信噪比$(SNR)_i$和輸出信噪比$(SNR)_o$的比值。數學上，它可以表示為：

$$F=\frac{(SNR)_i}{(SNR)_o}$$

$$\Rightarrow F=\frac{S_i/N_i}{S_o/N_o}$$

$$\Rightarrow F=\frac{N_oS_i}{N_iS_o}$$

$$\Rightarrow S_i=\frac{FN_iS_o}{N_o}$$

將$N_i=KT_oB_n$代入上述方程。

$$\Rightarrow S_i=FKT_oB_n\left ( \frac{S_o}{N_o}\right )$$

當輸出信噪比最小值時，輸入訊號功率將具有最小值。

$$\Rightarrow S_{min}=FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}$$

將上述$S_{min}$代入雷達距離方程的以下標準形式。

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}}\right ]^{1/4}$$

從上述方程，我們可以得出結論，為了使雷達的探測距離最大化，應考慮以下條件。

• 雷達發射的峰值功率$P_t$應很高。
• 發射天線的增益$G$應很高。
• 目標的雷達截面$\sigma$應很高。
• 接收天線的有效孔徑$A_e$應很高。
• 品質因數F應很低。
• 接收機頻寬$B_n$應很低。

雷達系統 - 雷達型別

本章將簡要討論不同型別的雷達。本章簡要介紹了雷達的型別。根據雷達可以使用哪種型別的訊號，雷達可以分為以下兩種型別。

• 脈衝雷達
• 連續波雷達

現在，讓我們逐一討論這兩種型別的雷達。

脈衝雷達

使用脈衝訊號工作的雷達稱為脈衝雷達。根據其檢測的目標型別，脈衝雷達可以分為以下兩種型別。

• 基本脈衝雷達
• 動目標指示雷達

現在讓我們簡要地討論這兩種雷達。

基本脈衝雷達

使用脈衝訊號檢測靜止目標的雷達稱為基本脈衝雷達或簡稱為脈衝雷達。它使用單個天線在雙工器的幫助下進行訊號的發射和接收。

天線將在每個時鐘脈衝發出脈衝訊號。兩個時鐘脈衝之間的時間間隔應選擇得當，以便在下一個時鐘脈衝之前接收當前時鐘脈衝對應的回波訊號。

動目標指示雷達

使用脈衝訊號檢測非靜止目標的雷達稱為動目標指示雷達或簡稱為MTI雷達。它使用單個天線在雙工器的幫助下進行訊號的發射和接收。

MTI雷達利用多普勒效應來區分非靜止目標和靜止物體。

連續波雷達

使用連續訊號或波工作的雷達稱為連續波雷達。它們使用多普勒效應來檢測非靜止目標。連續波雷達可以分為以下兩種型別。

• 非調製連續波雷達
• 調頻連續波雷達

現在，讓我們簡要地討論這兩種雷達。

非調製連續波雷達

使用連續訊號（波）檢測非靜止目標的雷達稱為非調製連續波雷達或簡稱為CW雷達。它也稱為CW多普勒雷達。

這種雷達需要兩個天線。這兩個天線中，一個天線用於發射訊號，另一個天線用於接收訊號。它只測量目標的速度，而不測量目標與雷達的距離。

調頻連續波雷達

如果CW多普勒雷達使用調頻，則該雷達稱為調頻連續波(FMCW)雷達或FMCW多普勒雷達。它也稱為連續波調頻雷達或CWFM雷達。

這種雷達需要兩個天線。其中一個天線用於發射訊號，另一個天線用於接收訊號。它不僅測量目標的速度，還測量目標與雷達的距離。

在我們接下來的章節中，我們將詳細討論所有這些雷達的操作。

雷達系統 - 脈衝雷達

使用脈衝訊號檢測靜止目標的雷達稱為基本脈衝雷達或簡稱為脈衝雷達。本章，我們將討論脈衝雷達的工作原理。

脈衝雷達的框圖

脈衝雷達使用單個天線在雙工器的幫助下進行訊號的發射和接收。以下是脈衝雷達的框圖：

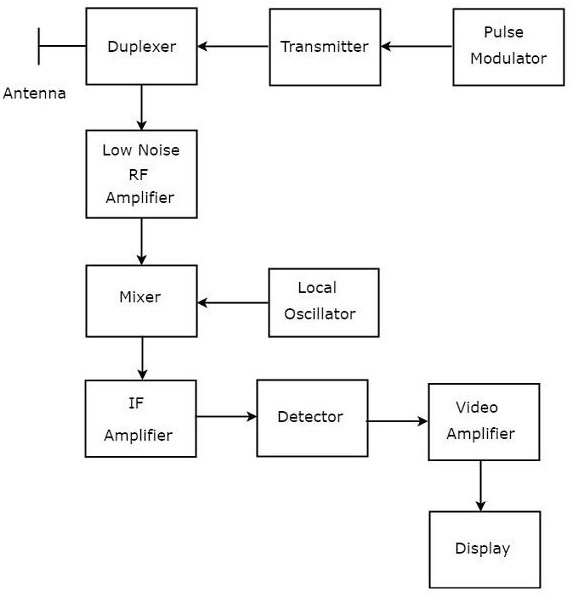
現在讓我們看看脈衝雷達每個模組的功能：

• 脈衝調製器 - 它產生脈衝調製訊號，並將其施加到發射機。

• 發射機 - 它發射脈衝調製訊號，這是一個重複脈衝序列。

• 雙工器 - 它是一個微波開關，可交替地將天線連線到發射部分和接收部分。當雙工器將天線連線到發射器時，天線發射脈衝調製訊號。類似地，當雙工器將天線連線到低噪聲射頻放大器時，天線接收到的訊號將被送入低噪聲射頻放大器。

• 低噪聲射頻放大器 - 它放大天線接收到的微弱射頻訊號。該放大器的輸出連線到混頻器。

• 區域性振盪器 - 它產生具有穩定頻率的訊號。區域性振盪器的輸出連線到混頻器。

• 混頻器 - 我們知道混頻器可以產生施加在其上的頻率的和與差。其中，頻率的差將是中頻 (IF) 型別。

• 中頻放大器 - 中頻放大器放大中頻 (IF) 訊號。圖中所示的中頻放大器只允許來自混頻器並放大從中頻，它提高了輸出端的信噪比。

• 檢波器 - 它解調從中頻放大器輸出獲得的訊號。

• 影片放大器 - 顧名思義，它放大從檢波器輸出獲得的影片訊號。

• 顯示器 - 通常，它在 CRT 螢幕上顯示放大的影片訊號。

本章討論了脈衝雷達的工作原理及其在探測靜止目標方面的用途。在接下來的章節中，我們將討論用於探測非靜止目標的雷達。

雷達系統 - 多普勒效應

本章我們將學習雷達系統中的多普勒效應。

如果目標不是靜止的，則從雷達發射並被雷達接收的訊號頻率將發生變化。這種效應稱為多普勒效應。

根據多普勒效應，我們將得到以下兩種可能的情況：

• 當目標朝向雷達方向移動時，接收訊號的頻率將增加。

• 當目標遠離雷達移動時，接收訊號的頻率將降低。

現在，讓我們推匯出多普勒頻率的公式。

多普勒頻率的推導

雷達與目標之間的距離就是目標的距離或簡稱為距離 R。因此，在雙向通訊路徑中，雷達與目標之間的總距離將為 2R，因為雷達向目標發射訊號，目標相應地向雷達傳送回波訊號。

如果 λ 是一個波長，則在雷達和目標之間的雙向通訊路徑中存在的波長數 N 將等於 2R/λ。

我們知道一個波長 λ 對應於 2π 弧度的角度偏移。因此，電磁波在雷達和目標之間的雙向通訊路徑中所做的總角度偏移將等於 4πR/λ 弧度。

以下是角頻率 ω 的數學公式：

$$\omega=2\pi f\:\:\:\:\:公式\:1$$

以下等式顯示了角頻率 ω 和相位角 φ 之間的數學關係：

$$\omega=\frac{d\phi }{dt}\:\:\:\:\:公式\:2$$

由於這兩個等式的左側項相同，因此使公式 1 和公式 2 的右側項相等。

$$2\pi f=\frac{d\phi }{dt}$$

$$\Rightarrow f =\frac{1}{2\pi}\frac{d\phi }{dt}\:\:\:\:\:公式\:3$$

代入，f=fd 和 φ=4πR/λ 到公式 3 中。

$$f_d =\frac{1}{2\pi}\frac{d}{dt}\left ( \frac{4\pi R}{\lambda} \right )$$

$$\Rightarrow f_d =\frac{1}{2\pi}\frac{4\pi}{\lambda}\frac{dR}{dt}$$

$$\Rightarrow f_d =\frac{2V_r}{\lambda}\:\:\:\:\:公式\:4$$

其中，

fd 是多普勒頻率

Vr 是相對速度

我們可以透過將 Vr 和 λ 的值代入公式 4 來找到多普勒頻率 fd 的值。

代入，λ=C/f 到公式 4 中。

$$f_d =\frac{2V_r}{C/f}$$

$$\Rightarrow f_d =\frac{2V_rf}{C}\:\:\:\:\:公式\:5$$

其中，

f 是發射訊號的頻率

C 是光速，等於 3×10^8m/sec

我們可以透過將 Vr、f 和 C 的值代入公式 5 來找到多普勒頻率 fd 的值。

注意 - 公式 4 和公式 5 都顯示了多普勒頻率 fd 的公式。我們可以根據給定的資料使用公式 4 或公式 5 來查詢多普勒頻率 fd。

例題

如果雷達以 5GHz 的頻率工作，則求以 100 公里/小時的速度移動的飛機的多普勒頻率。

解答

已知：

發射訊號的頻率，f=5GHz

飛機（目標）的速度，Vr=100 公里/小時

$$\Rightarrow V_r=\frac{100\times 10^3}{3600}m/sec$$

$$\Rightarrow V_r=27.78m/sec$$

我們已經將給定的飛機（目標）速度（以公里/小時為單位）轉換為等效的米/秒。

我們知道，光速 C=3×10^8m/sec

現在，以下是多普勒頻率公式：

$$f_d=\frac{2Vrf}{C}$$

代入上述等式中 Vr、f 和 C 的值。

$$\Rightarrow f_d=\frac{2\left ( 27.78 \right )\left ( 5\times 10^9 \right )}{3\times 10^8}$$

$$\Rightarrow f_d=926HZ$$

因此，對於給定的規格，多普勒頻率 fd 的值為 926Hz。

雷達系統 - 連續波雷達

基本雷達使用相同的天線進行訊號的發射和接收。當目標靜止（即不移動）和/或雷達可以使用脈衝訊號工作時，我們可以使用這種型別的雷達。

使用連續訊號（波）探測非靜止目標的雷達稱為連續波雷達或簡稱為CW 雷達。這種雷達需要兩個天線。其中一個天線用於發射訊號，另一個天線用於接收訊號。

CW 雷達的框圖

我們知道 CW 多普勒雷達包含兩個天線：發射天線和接收天線。下圖顯示了 CW 雷達的框圖：

CW 多普勒雷達的框圖包含一組模組，每個模組的功能如下所述。

• CW 發射器 - 它產生頻率為 fo 的模擬訊號。CW 發射器的輸出連線到發射天線和混頻器 I。

• 區域性振盪器 - 它產生頻率為 fl 的訊號。區域性振盪器的輸出連線到混頻器 I。

• 混頻器 I - 混頻器可以產生施加在其上的頻率的和與差。頻率為 fo 和 fl 的訊號施加到混頻器 I。因此，混頻器 I 將產生頻率為 fo+fl 或 fo−fl 的輸出。

• 邊帶濾波器 - 顧名思義，邊帶濾波器允許特定的邊帶頻率 - 上邊帶頻率或下邊帶頻率。上圖所示的邊帶濾波器僅產生上邊帶頻率，即 fo+fl。

• 混頻器 II - 混頻器可以產生施加在其上的頻率的和與差。頻率為 fo+fl 和 fo±fd 的訊號施加到混頻器 II。因此，混頻器 II 將產生頻率為 2fo+fl±fd 或 fl±fd 的輸出。

• 中頻放大器 - 中頻放大器放大中頻 (IF) 訊號。圖中所示的中頻放大器只允許中頻 fl±fd 並放大它。

• 檢波器 - 它檢測具有多普勒頻率 fd 的訊號。

• 多普勒放大器 - 顧名思義，多普勒放大器放大具有多普勒頻率 fd 的訊號。

• 指示器 - 它指示與相對速度相關的信以及目標是入站還是出站的資訊。

CW 多普勒雷達可以精確測量相對速度。因此，它們主要用於速度資訊比實際距離更重要的場合。

雷達系統 - 調頻連續波雷達

如果 CW 多普勒雷達使用頻率調製，則該雷達稱為 FMCW多普勒雷達或簡稱為FMCW 雷達。它也稱為連續波調頻雷達或 CWFM 雷達。它不僅測量目標的速度，還測量目標與雷達之間的距離。

FMCW 雷達的框圖

FMCW 雷達主要用作雷達高度計，以便在飛機著陸時測量精確高度。下圖顯示了 FMCW 雷達的框圖：

FMCW 雷達包含兩個天線：發射天線和接收天線，如圖所示。發射天線發射訊號，接收天線接收回波訊號。

FMCW 雷達的框圖與 CW 雷達的框圖類似。除了 CW 雷達框圖中存在的模組外，它還包含一些修改後的模組和一些其他模組。FMCW 雷達每個模組的功能如下所述。

• 調頻調製器 - 它產生具有可變頻率 fo(t) 的調頻 (FM) 訊號，並將其應用於調頻發射器。

• 調頻發射器 - 它藉助發射天線發射調頻訊號。調頻發射器的輸出也連線到混頻器 I。

• 區域性振盪器 - 通常，區域性振盪器用於產生射頻訊號。但是，在這裡它用於產生具有中頻 fIF 的訊號。區域性振盪器的輸出連線到混頻器 I 和平衡檢波器。

• 混頻器 I - 混頻器可以產生施加在其上的頻率的和與差。頻率為 fo(t) 和 fIF 的訊號施加到混頻器 I。因此，混頻器 I 將產生頻率為 fo(t)+fIF 或 fo(t)-fIF 的輸出。

• 邊帶濾波器 - 它只允許一個邊帶頻率，即上邊帶頻率或下邊帶頻率。圖中所示的邊帶濾波器只產生下邊帶頻率，即 fo(t)-fIF。

• 混頻器-II − 混頻器可以產生施加在其上的頻率的和與差。頻率為 $f_o\left (t \right )-f_{IF}$ 和 $f_o\left (t-T \right )$ 的訊號施加到混頻器-II。因此，混頻器-II 將產生頻率為 $f_o\left (t-T \right )+f_o\left (t \right )-f_{IF}$ 或 $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$ 的輸出。

• 中頻放大器 − 中頻放大器放大中頻 (IF) 訊號。圖中所示的中頻放大器放大頻率為 $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$ 的訊號。該放大訊號作為輸入施加到平衡檢波器。

• 平衡檢波器 − 它用於從施加的兩個輸入訊號（頻率為 $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$ 和 $f_{IF}$）產生頻率為 $f_o\left (t-T \right )-f_o\left (t \right )$ 的輸出訊號。平衡檢波器的輸出作為輸入施加到低頻放大器。

• 低頻放大器 − 它將平衡檢波器的輸出放大到所需電平。低頻放大器的輸出施加到開關頻率計數器和平均頻率計數器。

• 開關頻率計數器 − 它用於獲取多普勒速度的值。

• 平均頻率計數器 − 它用於獲取距離的值。

雷達系統 - MTI 雷達

如果雷達用於檢測移動目標，則雷達應僅接收由於該移動目標造成的回波訊號。該回波訊號是期望訊號。然而，在實際應用中，雷達除了接收由於該移動目標造成的回波訊號外，還接收由於靜止物體造成的回波訊號。

由於靜止物體（場所）如陸地和海洋造成的回波訊號稱為雜波，因為這些是不需要的訊號。因此，我們必須選擇雷達，使其僅考慮由於移動目標造成的回波訊號，而不考慮雜波。

為此目的，雷達利用多普勒效應的原理來區分非靜止目標與靜止物體。這種型別的雷達稱為移動目標指示雷達，或簡稱為MTI 雷達。

根據多普勒效應，如果目標朝向雷達方向移動，則接收訊號的頻率將增加。同樣，如果目標遠離雷達移動，則接收訊號的頻率將降低。

MTI 雷達的型別

我們可以根據所使用的發射機的型別將 MTI 雷達分為以下兩種型別。

• 採用功率放大器發射機的 MTI 雷達
• 採用功率振盪器發射機的 MTI 雷達

現在，讓我們逐一討論這兩種 MTI 雷達。

採用功率放大器發射機的 MTI 雷達

MTI 雷達使用單個天線在雙工器的幫助下進行訊號的發射和接收。採用功率放大器發射機的 MTI 雷達的框圖如下所示。（此處應插入框圖）

採用功率放大器發射機的 MTI 雷達中每個模組的功能如下所述。

• 脈衝調製器 − 它產生脈衝調製訊號，並將其施加到功率放大器。

• 功率放大器 − 它放大脈衝調製訊號的功率電平。

• 區域性振盪器 − 它產生具有穩定頻率 $f_l$ 的訊號。因此，它也稱為穩定區域性振盪器。區域性振盪器的輸出施加到混頻器-I 和混頻器-II。

• 相干振盪器 − 它產生具有中頻 $f_c$ 的訊號。該訊號用作參考訊號。相干振盪器的輸出施加到混頻器-I 和相位檢測器。

• 混頻器-I − 混頻器可以產生施加在其上的頻率的和或差。頻率為 $f_l$ 和 $f_c$ 的訊號施加到混頻器-I。此處，混頻器-I 用於產生頻率為 $f_l+f_c$ 的輸出。

• 雙工器 − 它是一個微波開關，根據需要將天線連線到發射部分或接收部分。當天線連線到功率放大器時，天線發射頻率為 $f_l+f_c$ 的訊號。同樣，當天線連線到混頻器-II 時，天線接收頻率為 $f_l+f_c\pm f_d$ 的訊號。

• 混頻器-II − 混頻器可以產生施加在其上的頻率的和或差。頻率為 $f_l+f_c\pm f_d$ 和 $f_l$ 的訊號施加到混頻器-II。此處，混頻器-II 用於產生頻率為 $f_c\pm f_d$ 的輸出。

• 中頻放大器 − 中頻放大器放大中頻 (IF) 訊號。圖中所示的中頻放大器放大頻率為 $f_c+f_d$ 的訊號。該放大訊號作為輸入施加到相位檢測器。

相位檢測器 − 它用於從施加的兩個輸入訊號（頻率為 $f_c+f_d$ 和 $f_c$）產生頻率為 $f_d$ 的輸出訊號。相位檢測器的輸出可以連線到延遲線抵消器。

採用功率振盪器發射機的 MTI 雷達

採用功率振盪器發射機的 MTI 雷達的框圖與採用功率放大器發射機的 MTI 雷達的框圖相似。接收部分對應的模組在兩個框圖中是相同的。而發射部分對應的模組在兩個框圖中可能不同。

採用功率振盪器發射機的 MTI 雷達的框圖如下所示。（此處應插入框圖）

如圖所示，MTI 雷達在雙工器的幫助下使用單個天線進行訊號的發射和接收。採用功率振盪器發射機的 MTI 雷達的工作原理如下所述。

• 磁控管振盪器的輸出和區域性振盪器的輸出施加到混頻器-I。這將進一步產生一個中頻訊號，其相位與發射訊號的相位直接相關。

• 混頻器-I 的輸出施加到相干振盪器。因此，相干振盪器輸出的相位將鎖定到中頻訊號的相位。這意味著相干振盪器輸出的相位也將與發射訊號的相位直接相關。

• 因此，相干振盪器的輸出可以用作參考訊號，用於使用相位檢測器將接收到的回波訊號與相應的發射訊號進行比較。

對於每個新發射的訊號，上述任務將重複執行。

雷達系統 - 延遲線抵消器

在本章中，我們將學習雷達系統中的延遲線抵消器。顧名思義，延遲線引入一定量的延遲。因此，延遲線主要用於延遲線抵消器中，以引入脈衝重複時間的延遲。

延遲線抵消器是一種濾波器，它消除從靜止目標接收到的回波訊號的直流分量。這意味著它允許從非靜止目標（即移動目標）接收到的回波訊號的交流分量。

延遲線抵消器的型別

可以根據其中存在的延遲線的數量將延遲線抵消器分為以下兩種型別。

• 單延遲線抵消器
• 雙延遲線抵消器

在我們接下來的章節中，我們將更詳細地討論這兩種延遲線抵消器。

單延遲線抵消器

延遲線和減法器的組合稱為延遲線抵消器。它也稱為單延遲線抵消器。具有單延遲線抵消器的 MTI 接收器的框圖如下所示。（此處應插入框圖）

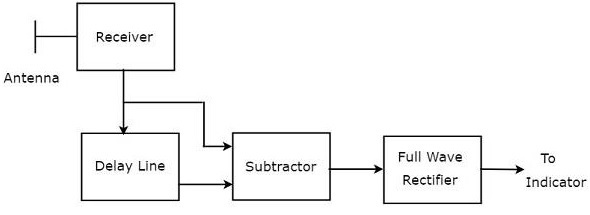
我們可以寫出多普勒效應後接收到的回波訊號的數學方程為：

$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:公式\:1$$

其中，

A 是影片訊號的幅度

fd 是多普勒頻率

$\phi_o$ 是相移，等於 $4\pi f_tR_o/C$

我們將透過在公式 1 中用 $t-T_P$ 代替 $t$ 來得到延遲線抵消器的輸出。

$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:公式\:2$$

其中，

$T_P$ 是脈衝重複時間

我們將透過從公式 1 中減去公式 2 來得到減法器的輸出。

$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2}\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$

$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\phi_0}{2} \right ]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:公式\:3$$

減法器的輸出作為輸入施加到全波整流器。因此，全波整流器的輸出看起來如下圖所示。它只不過是單延遲線抵消器的頻率響應。（此處應插入頻率響應圖）

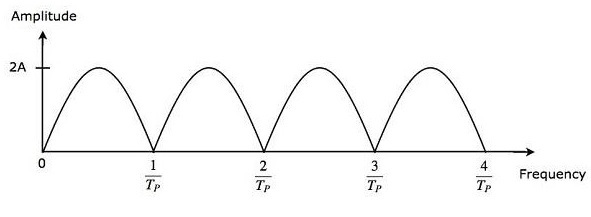
從公式 3，我們可以觀察到，當 $\pi f_dT_P$ 等於π 的整數倍時，單延遲線抵消器的頻率響應變為零。這意味著 $\pi f_dT_P$ 等於 $n\pi$。數學上，它可以寫成

$$\pi f_dT_P=n\pi$$

$$\Rightarrow f_dT_P=n$$

$$\Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:公式\:4$$

從公式 4，我們可以得出結論，當多普勒頻率 $f_d$ 等於脈衝重複時間 $T_P$ 倒數的整數倍時，單延遲線抵消器的頻率響應變為零。

我們知道脈衝重複時間和脈衝重複頻率之間的以下關係。

$$f_d=\frac{1}{T_P}$$

$$\Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:公式\:5$$

我們將透過在公式 4 中代入公式 5 來得到以下公式。

$$\Rightarrow f_d=nf_P\:\:\:\:\:公式\:6$$

從公式 6，我們可以得出結論，當多普勒頻率 $f_d$ 等於脈衝重複頻率 $f_P$ 的整數倍時，單延遲線抵消器的頻率響應變為零。

盲速

從我們目前學到的內容來看，當 n 等於零時，單延遲線抵消器消除從靜止目標接收到的回波訊號的直流分量。除此之外，當多普勒頻率 $f_d$ 等於脈衝重複頻率 $f_P$ 的整數（非零）倍時，它還消除從非靜止目標接收到的回波訊號的交流分量。

因此，單延遲線抵消器的頻率響應變為零的相對速度稱為盲速。數學上，我們可以將盲速 $v_n$ 的表示式寫為：

$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:公式\:7$$

$$\Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:公式\:8$$

其中，

$n$ 是整數，等於 1、2、3 等

$\lambda$ 是工作波長

例題

一個 MTI 雷達以 6GHz 的頻率和 1kHz 的脈衝重複頻率工作。求該雷達的第一、第二和第三盲速。

解答

已知：

MTI 雷達的工作頻率，$f=6GHZ$

脈衝重複頻率，$f_P=1KHZ$。

以下是根據工作頻率 f 計算工作波長 $\lambda$ 的公式。

$$\lambda=\frac{C}{f}$$

在上述公式中代入 $C=3\times10^8m/sec$ 和 $f=6GHZ$。

$$\lambda=\frac{3\times10^8}{6\times10^9}$$

$$\Rightarrow \lambda=0.05m$$

因此，當工作頻率 f 為 6GHz 時，工作波長 $\lambda$ 等於 0.05m。

我們知道盲速公式如下。

$$v_n=\frac{n\lambda f_p}{2}$$

將上述方程中的 $n$ 分別代入 1、2 和 3，我們將得到第一、第二和第三盲速的方程。

$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$

$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$

$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$

將 $\lambda$ 和 $f_P$ 的值代入第一盲速方程。

$$v_1=\frac{0.05\times 10^3}{2}$$

$$\Rightarrow v_1=25m/sec$$

因此，對於給定的引數，第一盲速 $v_1$ 等於 $25m/sec$。

透過將 $v_1$ 的值代入第二和第三盲速方程，我們將得到第二和第三盲速的值分別為 $50m/sec$ 和 $75m/sec$。

雙延遲線抵消器

我們知道，單個延遲線抵消器由延遲線和減法器組成。如果將兩個這樣的延遲線抵消器級聯在一起，則該組合稱為雙延遲線抵消器。雙延遲線抵消器的框圖如下所示。

設 $p\left ( t \right )$ 和 $q\left ( t \right )$ 分別為第一延遲線抵消器的輸入和輸出。我們將從第一延遲線抵消器得到以下數學關係。

$$q\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )\:\:\:\:\:公式\:9$$

第一延遲線抵消器的輸出作為第二延遲線抵消器的輸入。因此，$q\left ( t \right )$ 將成為第二延遲線抵消器的輸入。設 $r\left ( t \right )$ 為第二延遲線抵消器的輸出。我們將從第二延遲線抵消器得到以下數學關係。

$$r\left ( t \right )=q\left ( t \right )-q\left ( t-T_P \right )\:\:\:\:\:公式\:10$$

在公式 9 中將 $t$ 替換為 $t-T_P$。

$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-T_P-T_P \right )$$

$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-2T_P \right )\:\:\:\:\:公式\:11$$

將公式 9 和公式 11 代入公式 10。

$$r\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )-\left [ p\left ( t-T_P \right )-p\left ( t-2T_P \right ) \right ]$$

$$\Rightarrow r\left ( t \right )=p\left ( t \right )-2p\left ( t-T_P \right )+p\left ( t-2T_P \right )\:\:\:\:\:公式\:12$$

雙延遲線抵消器的優點是它可以廣泛地抑制雜波。兩個級聯的延遲線抵消器的輸出將等於單個延遲線抵消器輸出的平方。

因此，存在於MTI雷達接收機的雙延遲線抵消器輸出的幅度將等於 $4A^2\left ( \sin\left [ \pi f_dT_P \right ] \right )^2$。

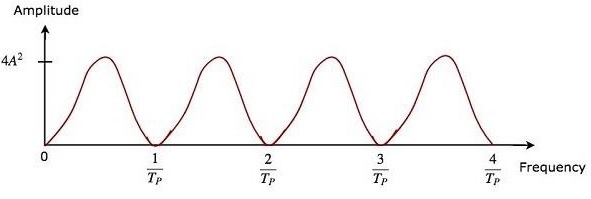
雙延遲線抵消器和兩個延遲線抵消器的級聯組合的頻率響應特性相同。時域延遲線抵消器的優點是它可以用於所有頻率範圍。

雷達系統 - 跟蹤雷達

用於跟蹤一個或多個目標軌跡的雷達稱為跟蹤雷達。通常，它會在開始跟蹤活動之前執行以下功能。

• 目標探測
• 目標距離
• 查詢仰角和方位角
• 查詢多普勒頻移

因此，跟蹤雷達透過跟蹤三個引數之一——距離、角度、多普勒頻移——來跟蹤目標。大多數跟蹤雷達使用角度跟蹤原理。現在，讓我們討論什麼是角度跟蹤。

角度跟蹤

雷達天線的窄波束進行角度跟蹤。雷達天線的軸線被認為是參考方向。如果目標方向和參考方向不相同，則將存在角度誤差，它不過是兩個方向之間的差值。

如果將角度誤差訊號施加到伺服控制系統，則它將使雷達天線的軸線向目標方向移動。當角度誤差為零時，雷達天線的軸線和目標方向將重合。跟蹤雷達中存在一個反饋機制，該機制一直工作到角度誤差變為零為止。

以下是角度跟蹤中使用的兩種技術。

• 順序波瓣
• 錐形掃描

現在，讓我們逐一討論這兩種技術。

順序波瓣

如果天線波束在兩個圖案之間交替切換以跟蹤目標，則稱為順序波瓣。它也稱為順序切換和波瓣切換。此技術用於查詢一個座標中的角度誤差。它提供了角度誤差的幅度和方向的詳細資訊。

下圖顯示了極座標系中順序波瓣的一個示例。

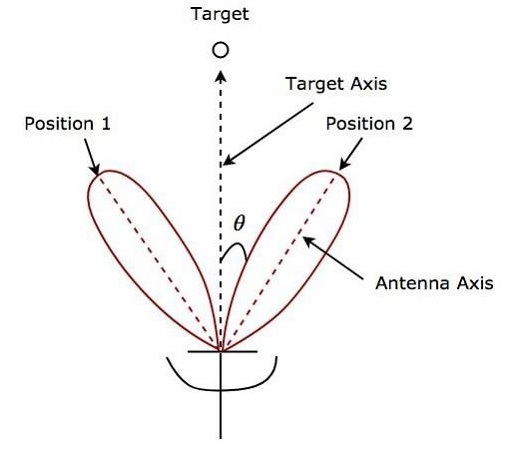
如圖所示，天線波束在位置 1 和位置 2 之間交替切換。上圖中指示了角度誤差 θ。順序波瓣以高精度給出目標的位置。這是順序波瓣的主要優點。

錐形掃描

如果天線波束連續旋轉以跟蹤目標，則稱為錐形掃描。錐形掃描調製用於查詢目標的位置。下圖顯示了錐形掃描的一個示例。

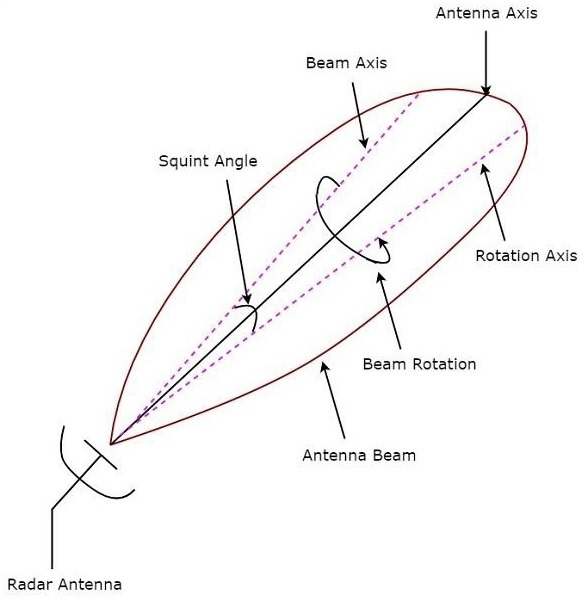
偏角是波束軸和旋轉軸之間的角度，它在上圖中顯示。從目標獲得的回波訊號以等於天線波束旋轉頻率的頻率進行調製。

目標方向與旋轉軸之間的角度決定了調製訊號的幅度。因此，必須從回波訊號中提取錐形掃描調製，然後將其施加到伺服控制系統，該系統將天線波束軸向目標方向移動。

雷達系統 - 天線引數

天線或天線是一種換能器，它將電能轉換成電磁波，反之亦然。

天線具有以下引數：

• 方向性
• 孔徑效率
• 天線效率
• 增益

現在，讓我們詳細討論這些引數：

方向性

根據標準定義，“被測天線最大輻射強度與輻射相同總功率的各向同性或參考天線的輻射強度的比值稱為方向性。”

雖然天線輻射功率，但其輻射方向的意義非常重大。正在研究的天線被稱為被測天線。它的輻射強度集中在特定方向，同時進行發射或接收。因此，據說天線在該特定方向上具有方向性。

• 天線在給定方向上的輻射強度與所有方向上的平均輻射強度的比值稱為方向性。

• 如果沒有指定該特定方向，則可以將觀察到最大強度的方向作為該天線的方向性。

• 非各向同性天線的方向性等於給定方向上的輻射強度與各向同性源的輻射強度的比值。

數學上，我們可以將方向性的表示式寫為：

$$方向性=\frac{U_{Max}\left (\theta,\phi\right )}{U_0}$$

其中，

$U_{Max}\left (\theta,\phi\right )$ 是被測天線最大輻射強度

$U_0$ 是各向同性天線的輻射強度。

孔徑效率

根據標準定義，“天線的孔徑效率是指有效輻射面積（或有效面積）與孔徑物理面積的比值。”

天線透過孔徑輻射功率。這種輻射應該有效，損失最小。還應考慮孔徑的物理面積，因為輻射的有效性取決於天線上物理孔徑的面積。

數學上，我們可以將孔徑效率 $\epsilon_A$ 的表示式寫為

$$\epsilon _A=\frac{A_{eff}}{A_p}$$

其中，

$A_{eff}$ 是有效面積

$A_P$ 是物理面積

天線效率

根據標準定義，“天線效率是指天線輻射功率與天線接收輸入功率的比值。”

任何天線的設計都是為了在給定輸入的情況下以最小的損耗輻射功率。天線的效率解釋了天線能夠多有效地傳遞其輸出，同時在傳輸線中損失最小。它也稱為天線的輻射效率因子。

數學上，我們可以將天線效率 $\eta_e$ 的表示式寫為：

$$\eta _e=\frac{P_{Rad}}{P_{in}}$$

其中，

$P_{Rad}$ 是輻射功率

$P_{in}$ 是天線的輸入功率

增益

根據標準定義，“天線的增益是指給定方向上的輻射強度與如果天線接收的功率被各向同性輻射所獲得的輻射強度的比值。”

簡而言之，天線的增益考慮了天線的方向性和有效效能。如果天線接收的功率被各向同性地輻射（即向所有方向輻射），則我們可以將獲得的輻射強度作為參考值。

• 術語天線增益描述了在峰值輻射方向上與各向同性源相比傳輸的功率。

• 增益通常以dB為單位測量。

• 與方向性不同，天線增益還考慮了發生的損耗，因此側重於效率。

數學上，我們可以將天線增益 $G$ 的表示式寫為：

$$G=\eta_eD$$

其中，

$\eta_e$ 是天線效率

$D$ 是天線的方向性

雷達系統 - 雷達天線

在本章中，讓我們學習在雷達通訊中很有用的天線。我們可以根據物理結構將雷達天線分為以下兩種型別。

• 拋物面反射器天線
• 透鏡天線

接下來的章節將詳細討論兩種型別的antenna。

拋物面反射器天線

拋物面反射器天線是微波天線。瞭解拋物面反射器的原理對於深入理解天線的工作原理至關重要。

工作原理

拋物線是指這樣一些點的軌跡：這些點到一個固定點（稱為焦點）的距離加上到一條直線（稱為準線）的距離是常數。

下圖顯示了拋物面反射器的幾何形狀。F點和V點分別是焦點（饋電點）和頂點。連線F和V的線是其對稱軸。$P_1Q_1, P_2Q_2$和$P_3Q_3$是反射光線。L線代表準線，反射點位於該線上（表示它們共線）。

如圖所示，F點和L線之間的距離相對於被聚焦的波是恆定的。反射波形成一個來自拋物面形狀的準直波陣面。焦距與孔徑尺寸之比（即$f/D$）被稱為“f/D比”。它是拋物面反射器的一個重要引數，其值範圍為0.25到0.50。

反射定律指出，入射角和反射角相等。該定律與拋物線一起使用有助於聚焦波束。拋物線的形狀用於反射波時，體現了拋物線的一些特性，這些特性有助於利用反射波構建天線。

拋物線的特性

以下是拋物線的不同特性：

• 所有從焦點發出的波都反射回拋物線軸。因此，到達孔徑的所有波都同相。

• 由於波是同相的，沿拋物線軸的輻射波束將強且集中。

基於這些特性，拋物面反射器有助於產生高方向性並具有更窄的波束寬度。

拋物面反射器的構造和工作原理

如果拋物面反射器天線用於發射訊號，則來自饋電器的訊號會從偶極子天線或喇叭天線發出，以將波聚焦到拋物面上。這意味著波從焦點發出並撞擊拋物面反射器。然後，該波如前所述被反射為準直波陣面，從而被髮射出去。

同一根天線用作接收器。當電磁波撞擊拋物面的形狀時，波被反射到饋電點。作為接收天線的饋電處的偶極子天線或喇叭天線接收此訊號，將其轉換為電訊號並將其轉發到接收電路。

拋物面的增益是孔徑比$D/\lambda$的函式。天線的有效輻射功率(ERP)是饋送到天線的輸入功率與其功率增益的乘積。

通常使用波導喇叭天線作為拋物面反射器天線的饋電輻射器。除了這種技術外，我們還有以下兩種型別的饋電方式提供給拋物面反射器天線。

• 卡塞格倫饋電
• 格里高利饋電

卡塞格倫饋電

在這種型別中，饋電器位於拋物面的頂點，與拋物面反射器不同。一個凸形反射器（充當雙曲線）放置在天線饋電器的對面。它也稱為次級雙曲線反射器或副反射器。它的位置使得它的一個焦點與拋物線的焦點重合。因此，波會反射兩次。

上圖顯示了卡塞格倫饋電的工作模型。

格里高利饋電

饋電型別中存在某些配置對，並且在保持天線尺寸不變的同時逐漸增加饋電波束寬度，稱為格里高利饋電。這裡，卡塞格倫的凸形雙曲線被一個凹形拋物面反射器所取代，該反射器的尺寸當然更小。

這些格里高利饋電型反射器可以透過以下四種方式使用：

• 使用焦點F1處的橢球副反射器的格里高利系統。

• 使用焦點F2處的橢球副反射器的格里高利系統。

• 使用雙曲線副反射器（凸）的卡塞格倫系統。

• 使用雙曲線副反射器（凹，但饋電器非常靠近它）的卡塞格倫系統。

在不同型別的反射器天線中，簡單的拋物面反射器和卡塞格倫饋電拋物面反射器是最常用的。

透鏡天線

透鏡天線使用曲面進行訊號的傳輸和接收。這些天線由玻璃製成，遵循透鏡的會聚和發散特性。透鏡天線的使用頻率範圍從1 GHz開始，但在3 GHz及以上頻率的使用更多。

需要了解透鏡的原理才能深入理解透鏡天線的工作原理。回想一下，普通的玻璃透鏡是基於折射原理工作的。

透鏡天線的構造和工作原理

如果假設在透鏡的焦點處存在一個光源，該光源距透鏡的焦距，則光線穿過透鏡後在平面波陣面上成為準直的或平行的光線。

當光線從透鏡的不同側面照射時，會發生兩種現象。它們如下：

• 穿過透鏡中心的光線比穿過透鏡邊緣的光線折射少。所有光線都平行於平面波陣面傳送。透鏡的這種現象稱為發散。

• 如果從右側向左側傳送光束，則相同的過程會反向進行。然後，光束髮生折射並在稱為焦點的點處相遇，該點距透鏡的焦距。這種現象稱為會聚。

下圖將幫助我們更好地理解這一現象。

光線圖表示從光源到透鏡的焦點和焦距。獲得的平行光線也稱為準直光線。

在上圖中，位於焦點處的光源（距透鏡的焦距）在平面波陣面上被準直。這種現象是可以反轉的，這意味著如果從左側傳送光線，則會在透鏡的右側會聚。

正是由於這種互易性，透鏡可以用作天線，因為相同的現象有助於利用相同的的天線進行傳輸和接收。

為了在較高頻率下實現聚焦特性，折射率應小於1。無論折射率是多少，透鏡的目的是使波形變直。基於此，開發了E平面和H平面透鏡，它們還可以延遲或加速波陣面。

雷達系統 - 匹配濾波器接收機

如果濾波器的輸出以最大化其頻率響應中輸出峰值功率與平均噪聲功率之比的方式產生，則該濾波器稱為匹配濾波器。

這是一個重要的標準，在設計任何雷達接收機時都會考慮。在本節中，我們將討論匹配濾波器的頻率響應函式和匹配濾波器的衝激響應。

匹配濾波器的頻率響應函式

匹配濾波器的頻率響應將與輸入訊號頻譜的共軛複數成正比。從數學上講，我們可以寫出匹配濾波器的頻率響應函式$H\left (f\right )$的表示式為：

$$H\left (f\right )=G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:公式\:1$$

其中，

$G_a$是匹配濾波器的最大增益

$S\left (f\right )$是輸入訊號$s\left (t\right )$的傅立葉變換

$S^\ast\left (f\right )$是$S\left (f\right )$的共軛複數

$t_1$是觀察到訊號最大值的時刻

一般情況下，$G_a$的值取為1。將$G_a=1$代入公式1，我們將得到以下公式：

$$H\left (f\right )=S^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:公式\:2$$

匹配濾波器的頻率響應函式$H\left (f\right )$具有$S^\ast\left (f\right )$的幅度和$e^{-j2\pi ft_1}$的相角，該相角隨頻率均勻變化。

匹配濾波器的衝激響應

在時域中，我們將透過對頻率響應函式$H(f)$進行逆傅立葉變換得到匹配濾波器接收機的輸出$h(t)$。

$$h\left (t\right )=\int_{-\infty }^{\infty }H\left (f\right )e^{-j2\pi ft_1}df\:\:\:\:\:公式\:3$$

將公式1代入公式3。

$$h\left (t\right )=\int_{-\infty }^{\infty }\lbrace G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\rbrace e^{j2\pi ft}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\ast\left (f\right )e^{-j2\pi f\left (t_1-t\right )}df\:\:\:\:\:公式\:4$$

我們知道以下關係。

$$S^\ast\left (f\right )=S\left (-f\right )\:\:\:\:\:公式\:5$$

將公式5代入公式4。

$$h\left (t\right )=\int_{-\infty }^{\infty }G_aS(-f)e^{-j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\left (f\right )e^{j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=G_as(t_1−t)\:\:\:\:\:公式\:6$$

一般情況下，$G_a$的值取為1。將$G_a=1$代入公式6，我們將得到以下公式：

$$h(t)=s\left (t_1-t\right )$$

上述公式證明了匹配濾波器的衝激響應是接收訊號關於時刻$t_1$的映象。下圖說明了這個概念。

上圖顯示了接收訊號$s\left (t\right )$和與訊號$s\left (t\right )$對應的匹配濾波器的衝激響應$h\left (t\right )$。

雷達系統 - 雷達顯示

用於以可視方式顯示資料的電子儀器稱為顯示器。因此，以可視方式顯示雷達目標資訊的電子儀器稱為雷達顯示器。它在螢幕上以可視方式顯示回波訊號資訊。

雷達顯示器的型別

在本節中，我們將學習不同型別的雷達顯示器。雷達顯示器可以分為以下型別。

A型顯示

這是一種二維雷達顯示器。水平和垂直座標分別表示目標的距離和回波幅度。在A型顯示中，發生偏轉調製。它更適合於手動跟蹤雷達。

B型顯示

這是一種二維雷達顯示器。水平和垂直座標分別表示目標的方位角和距離。在B型顯示中，發生強度調製。它更適合於軍用雷達。

C型顯示

這是一種二維雷達顯示器。水平和垂直座標分別表示方位角和仰角。在C型顯示中，發生強度調製。

D型顯示

如果由於目標的存在，電子束髮生偏轉或強度調製的光點出現在雷達顯示器上，則稱為亮點。當亮點垂直延伸以提供距離時，C型顯示變為D型顯示。

E型顯示

這是一種二維雷達顯示器。水平和垂直座標分別表示距離和仰角。在E型顯示中，發生強度調製。

F型顯示

如果雷達天線瞄準目標，則F型顯示將目標顯示為中心亮點。因此，亮點的水平和垂直位移分別表示水平和垂直瞄準誤差。

G型顯示

如果雷達天線瞄準目標，則G型顯示將目標顯示為橫向中心亮點。亮點的水平和垂直位移分別表示水平和垂直瞄準誤差。

H型顯示

這是B型顯示的改進版本，用於提供目標仰角資訊。它將目標顯示為兩個緊密間隔的亮點。這可以近似為一條短的亮線，該線的斜率將與仰角的正弦成正比。

I型顯示

如果雷達天線指向目標，則I-Scope顯示目標為一個圓圈。該圓圈的半徑與目標的距離成正比。如果雷達天線指向目標不準確，則I-Scope顯示目標為一段弧線而不是圓圈。該弧線的長度與指向誤差的大小成反比。

J-Scope

它是A-Scope的改進版本。它將目標顯示為從時間基線發出的徑向偏轉。

K-Scope

它是A-Scope的改進版本。如果雷達天線指向目標，則K-Scope顯示目標為一對高度相等的垂直偏轉。如果雷達天線指向目標不準確，則會產生指向誤差。因此，指向誤差的大小和方向取決於這兩個垂直偏轉之間的差異。

L-Scope

如果雷達天線指向目標，則L-Scope顯示目標為兩個幅度相等的水平脈衝。一個水平脈衝位於中心垂直時間基線的右側，另一個位於中心垂直時間基線的左側。

M-Scope

它是A-Scope的改進版本。必須沿基線移動一個可調的基座訊號，直到它與來自目標水平位置的訊號偏轉重合。透過這種方式，可以確定目標的距離。

N-Scope

它是K-Scope的改進版本。使用可調的基座訊號來測量距離。

O-Scope

它是A-Scope的改進版本。透過在A-Scope中加入一個可調的缺口來測量距離，我們可以得到O-Scope。

P-Scope

這是一種使用強度調製的雷達顯示器。它以平面圖的形式顯示回波訊號的資訊。距離和方位角以極座標顯示。因此，它被稱為平面位置指示器或PPI顯示器。

R-Scope

這是一種使用強度調製的雷達顯示器。水平和垂直座標分別代表目標的距離和高度。因此，它被稱為距離-高度指示器或RHI顯示器。

雷達系統 - 雙工器

在雙向通訊中，如果我們應該使用相同的 antenna 來收發訊號，那麼我們需要雙工器。雙工器是一種微波開關，它在訊號傳輸時將天線連線到發射機部分。因此，雷達在傳輸期間無法接收訊號。

類似地，它在訊號接收時將天線連線到接收機部分。雷達在接收期間無法傳輸訊號。透過這種方式，雙工器隔離了發射機和接收機部分。

雙工器的型別

在本節中，我們將學習不同型別的雙工器。我們可以將雙工器分為以下三種類型。

• 支路型雙工器
• 平衡雙工器
• 環行器作為雙工器

在我們接下來的章節中，我們將詳細討論雙工器的型別。

支路型雙工器

支路型雙工器由兩個開關組成——收發開關（TR開關）和抗收發開關（ATR開關）。下圖顯示了支路型雙工器的框圖：

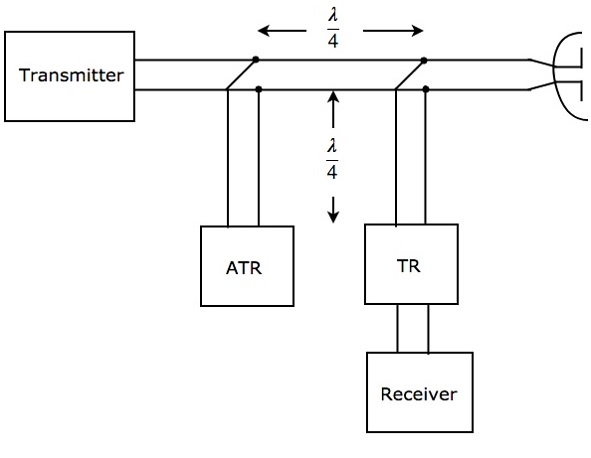
如圖所示，兩個開關TR和ATR與傳輸線相距λ/4，並且這兩個開關相距λ/4。支路型雙工器的工作原理如下。

• 在傳輸過程中，TR和ATR從傳輸線來看都像開路。因此，天線將透過傳輸線連線到發射機。

• 在接收過程中，ATR在傳輸線上看起來像短路。因此，天線將透過傳輸線連線到接收機。

支路型雙工器只適用於低成本雷達，因為它具有較低的功率處理能力。

平衡雙工器

我們知道，雙孔定向耦合器是一個四埠波導結，由一個主波導和一個次波導組成。有兩個小孔，這兩個波導將共用這兩個小孔。

平衡雙工器由兩個TR管組成。用於傳輸目的的平衡雙工器配置如下圖所示。

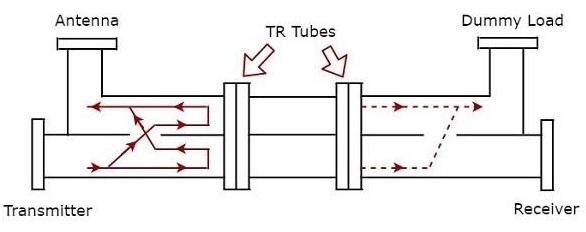
發射機產生的訊號必須到達天線，以便天線在傳輸期間傳輸該訊號。上圖中顯示的帶箭頭實線表示訊號如何從發射機到達天線。

上圖中顯示的帶箭頭虛線表示從雙TR管洩漏的訊號；這隻會到達匹配負載。因此，沒有訊號到達接收機。

用於接收目的的平衡雙工器配置如下圖所示。

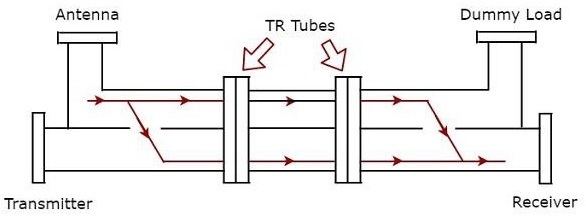
我們知道天線在接收期間接收訊號。天線接收到的訊號必須到達接收機。上圖中顯示的帶箭頭實線表示訊號如何從天線到達接收機。在這種情況下，雙TR管將訊號從波導的第一部分傳遞到波導的下一部分。

與支路型雙工器相比，平衡雙工器具有更高的功率處理能力和更高的頻寬。

環行器作為雙工器

我們知道環行器的功能是，如果我們將輸入應用於一個埠，它將在順時針方向相鄰的埠產生輸出。環行器的其餘埠沒有輸出。

因此，考慮一個四埠環行器，並將發射機、天線、接收機和匹配負載分別連線到埠1、埠2、埠3和埠4。現在，讓我們瞭解四埠環行器如何作為雙工器工作。

發射機產生的訊號必須到達天線，以便天線在傳輸期間傳輸該訊號。當發射機在埠1產生訊號時，將實現此目的。

天線接收到的訊號必須在接收期間到達接收機。當位於埠2的天線接收外部訊號時，將實現此目的。

下圖顯示了作為雙工器的環行器的框圖：

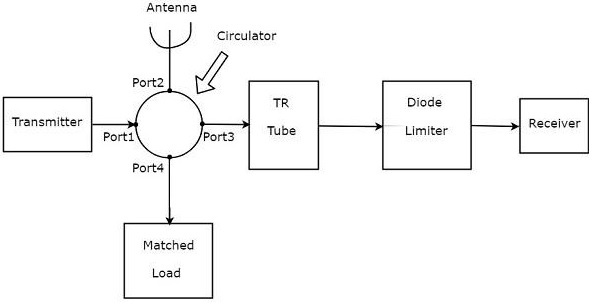
上圖由一個四埠環行器組成——發射機、天線和匹配負載分別連線到環行器的埠1、埠2和埠4，如本節開頭所述。

接收機沒有直接連線到埠3。相反，對應於無源TR限幅器的模組位於環行器的埠3和接收機之間。TR管和二極體限幅器是對應於無源TR限幅器的模組。

實際上，環行器本身充當雙工器。它不需要任何額外的模組。但是，它不會對接收機提供任何保護。因此，為了保護接收機，使用了對應於無源TR限幅器的模組。

雷達系統 - 相控陣天線

單個天線可以在特定方向輻射一定量的功率。顯然，當我們將多個天線組合在一起使用時，輻射功率會增加。天線組稱為天線陣列。

天線陣列是一個由輻射器和單元組成的輻射系統。每個輻射器都有其自身的感應場。這些單元放置得非常緊密，以至於每個單元都位於相鄰單元的感應場中。因此，它們產生的輻射影像是各個輻射影像的向量和。

天線單獨輻射，而在陣列中，所有單元的輻射相加，形成具有高增益、高方向性和更好效能且損耗最小的輻射波束。

如果輻射圖樣的形狀和方向取決於該陣列中每個天線的電流的相對相位和幅度，則稱天線陣列為相控陣天線陣列。

輻射圖樣

讓我們考慮“n”個各向同性輻射單元，當它們組合在一起時形成一個陣列。下圖將幫助您瞭解這一點。設相鄰單元之間的間距為“d”個單位。

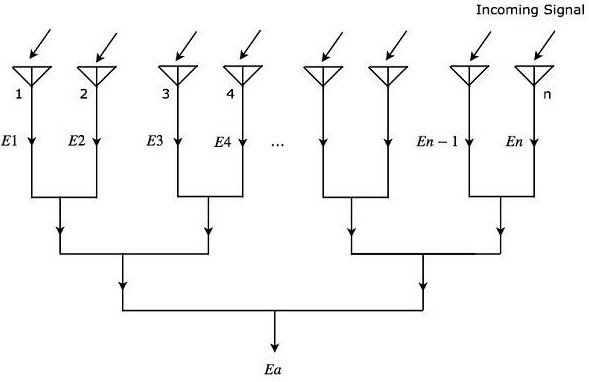
如圖所示，所有輻射單元都接收相同的入射訊號。因此，每個單元產生相同的輸出電壓sin(ωt)。但是，相鄰單元之間將存在相等的相位差Ψ。數學上，它可以寫成：

$$Ψ=\frac{2\pi d\sin\theta }{\lambda }\:\:\:\:\:公式\:1$$

其中，

θ是入射訊號入射到每個輻射單元的角度。

數學上，我們可以分別將“n”個輻射單元的輸出電壓表示式寫為

$$E_1=\sin\left [ \omega t \right]$$

$$E_2=\sin\left [\omega t+\Psi\right]$$

$$E_3=\sin\left [\omega t+2\Psi\right]$$

$$.$$

$$.$$

$$.$$

$$E_n=\sin\left [\omega t+\left (N-1\right )\Psi\right]$$

其中，

E₁、E₂、E₃……Eₙ分別是第一、第二、第三……n個輻射單元的輸出電壓。

ω是訊號的角頻率。

由於所有這些輻射單元都連線線上性陣列中，我們將透過將陣列中每個單元的輸出電壓相加來獲得陣列的總輸出電壓Ea。數學上，它可以表示為：

$$E_a=E_1+E_2+E_3+ …+E_n \:\:\:公式\:2$$

代入公式2中E₁、E₂、E₃……Eₙ的值。

$$E_a=\sin\left [ \omega t \right]+\sin\left [\omega t+\Psi\right ]+\sin\left [\omega t+2\Psi\right ]+\sin\left [\omega t+\left (n-1\right )\Psi\right]$$

$$\Rightarrow E_a=\sin\left [\omega t+\frac{(n-1)\Psi)}{2}\right ]\frac{\sin\left [\frac{n\Psi}{2}\right]}{\sin\left [\frac{\Psi}{2}\right ]}\:\:\:\:\:公式\:3$$

在公式3中，有兩個項。從第一項可以看出，總輸出電壓Ea是一個具有角頻率ω的正弦波。但是，它具有(n−1)Ψ/2的相移。公式3的第二項是幅度因子。

公式3的大小將為

$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\Psi}{2}\right ]}{\sin\left [\frac{\Psi}{2}\right]} \right |\:\:\:\:\:公式\:4$$

我們將透過將公式1代入公式4得到以下公式。

$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right]}{\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]} \right |\:\:\:\:\:公式\:5$$

公式5稱為場強圖樣。當公式5的分子為零時，場強圖樣將具有零值

$$\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right ]=0$$

$$\Rightarrow \frac{n\pi d\sin\theta}{\lambda}=\pm m\pi$$

$$\Rightarrow nd\sin\theta=\pm m\lambda$$

$$\Rightarrow \sin\theta=\pm \frac{m\lambda}{nd}$$

其中，

m是一個整數，等於1、2、3等等。

當公式5的分子和分母都等於零時，我們可以使用洛必達法則找到場強圖樣的最大值。我們可以觀察到，如果公式5的分母變為零，則公式5的分子也變為零。

現在，讓我們得到公式5的分母變為零的條件。

$$\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]=0$$

$$\Rightarrow \frac{\pi d\sin\theta}{\lambda}=\pm p\pi$$

$$\Rightarrow d\sin\theta=\pm p\lambda$$

$$\Rightarrow \sin\theta=\pm \frac{p\lambda}{d}$$

其中，

p是一個整數，等於0、1、2、3等等。

如果我們將p視為零，那麼我們將得到sinθ的值為零。對於這種情況，我們將得到對應於主瓣的場強圖樣的最大值。當我們考慮p的其他值時，我們將得到對應於旁瓣的場強圖樣的最大值。

相控陣的輻射方向可以透過改變每個天線上存在的電流的相對相位來控制。這是電子掃描相控陣的優勢。