
雷達系統 - 延遲線抵消器
本章將學習雷達系統中的延遲線抵消器。顧名思義,延遲線引入一定的延遲。因此,延遲線主要用於延遲線抵消器,以引入脈衝重複時間的延遲。
延遲線抵消器是一種濾波器,它消除來自靜止目標的回波訊號的直流分量。這意味著它允許來自非靜止目標(即移動目標)的回波訊號的交流分量透過。
延遲線抵消器的型別
根據延遲線數量的不同,延遲線抵消器可以分為以下兩種型別。
- 單延遲線抵消器
- 雙延遲線抵消器
在接下來的章節中,我們將更詳細地討論這兩種延遲線抵消器。
單延遲線抵消器
延遲線和減法器的組合稱為延遲線抵消器。它也稱為單延遲線抵消器。帶單延遲線抵消器的MTI接收機的框圖如下所示。(此處應插入圖片)
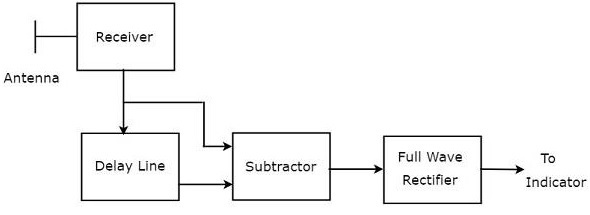
我們可以寫出多普勒效應後接收到的回波訊號的數學方程為:
$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:公式\:1$$
其中:
A 是影片訊號的幅度
$f_d$ 是多普勒頻率
$\phi_o$ 是相移,等於 $4\pi f_tR_o/C$
透過在公式1中用 $t-T_P$ 代替 $t$,我們將得到延遲線抵消器的輸出。
$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:公式\:2$$
其中:
$T_P$ 是脈衝重複時間
透過從公式1中減去公式2,我們將得到減法器的輸出。
$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$
$$ \Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2}\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$
$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\phi_0}{2} \right ]$$
$$ \Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:公式\:3$$
減法器的輸出作為輸入應用於全波整流器。因此,全波整流器的輸出如下所示。(此處應插入圖片)它只不過是單延遲線抵消器的頻率響應。
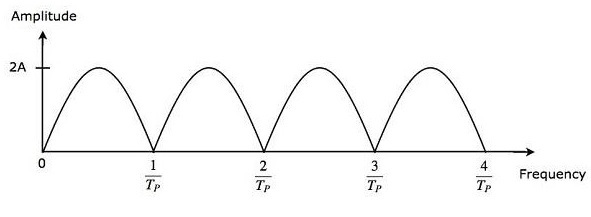
從公式3可以看出,當 $\pi f_dT_P$ 等於π 的整數倍時,單延遲線抵消器的頻率響應變為零。這意味著 $\pi f_dT_P$ 等於 $n\pi$。數學上,可以寫成:
$$ \pi f_dT_P=n\pi$$
$$ \Rightarrow f_dT_P=n$$
$$ \Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:公式\:4$$
從公式4可以得出結論,當多普勒頻率 $f_d$ 等於脈衝重複時間 $T_P$ 倒數的整數倍時,單延遲線抵消器的頻率響應變為零。
我們知道脈衝重複時間和脈衝重複頻率之間的以下關係。
$$f_d=\frac{1}{T_P}$$
$$ \Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:公式\:5$$
將公式5代入公式4,我們將得到以下公式。
$$ \Rightarrow f_d=nf_P\:\:\:\:\:公式\:6$$
從公式6可以得出結論,當多普勒頻率 $f_d$ 等於脈衝重複頻率 $f_P$ 的整數倍時,單延遲線抵消器的頻率響應變為零。
盲速
從我們目前所學,當 $n$ 等於零時,單延遲線抵消器消除來自靜止目標的回波訊號的直流分量。除此之外,當多普勒頻率 $f_d$ 等於脈衝重複頻率 $f_P$ 的整數(非零)倍時,它還會消除來自非靜止目標的回波訊號的交流分量。
因此,單延遲線抵消器的頻率響應變為零的相對速度稱為盲速。數學上,我們可以將盲速 $v_n$ 的表示式寫為:
$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:公式\:7$$
$$ \Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:公式\:8$$
其中:
$n$ 是整數,等於 1、2、3 等
$\lambda$ 是工作波長
例題
一臺MTI雷達工作頻率為$6GHZ$,脈衝重複頻率為$1KHZ$。求該雷達的一、二、三盲速。
解答
已知:
MTI雷達的工作頻率,$f=6GHZ$
脈衝重複頻率,$f_P=1KHZ$。
以下是根據工作頻率 f 計算工作波長 $\lambda$ 的公式。
$$ \lambda=\frac{C}{f}$$
在上述公式中代入 $C=3\times10^8m/sec$ 和 $f=6GHZ$。
$$ \lambda=\frac{3\times10^8}{6\times10^9}$$
$$ \Rightarrow \lambda=0.05m$$
因此,當工作頻率 f 為 $6GHZ$ 時,工作波長 $\lambda$ 等於 $0.05m$。
我們知道盲速公式如下:
$$v_n=\frac{n\lambda f_p}{2}$$
在上述公式中代入 $n$=1,2 & 3,我們將分別得到一、二、三盲速的以下公式。
$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$
$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$
$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$
在第一盲速公式中代入 $\lambda$ 和 $f_P$ 的值。
$$v_1=\frac{0.05\times 10^3}{2}$$
$$ \Rightarrow v_1=25m/sec$$
因此,對於給定的規格,第一盲速 $v_1$ 等於 $25m/sec$。
透過在第二和第三盲速公式中代入 𝑣1 的值,我們將分別得到第二和第三盲速的值為 $50m/sec$ 和 $75m/sec$。
雙延遲線抵消器
我們知道單延遲線抵消器由延遲線和減法器組成。如果將兩個這樣的延遲線抵消器級聯在一起,則該組合稱為雙延遲線抵消器。雙延遲線抵消器的框圖如下所示。(此處應插入圖片)

設 $p\left ( t \right )$ 和 $q\left ( t \right )$ 分別為第一個延遲線抵消器的輸入和輸出。我們將從第一個延遲線抵消器得到以下數學關係。
$$q\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )\:\:\:\:\:公式\:9$$
第一個延遲線抵消器的輸出作為輸入應用於第二個延遲線抵消器。因此,$q\left ( t \right )$ 將成為第二個延遲線抵消器的輸入。設 $r\left ( t \right )$ 為第二個延遲線抵消器的輸出。我們將從第二個延遲線抵消器得到以下數學關係。
$$r\left ( t \right )=q\left ( t \right )-q\left ( t-T_P \right )\:\:\:\:\:公式\:10$$
在公式9中將 $t$ 替換為 $t-T_P$。
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-T_P-T_P \right )$$
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-2T_P \right )\:\:\:\:\:公式\:11$$
在公式10中代入公式9和公式11。
$$r\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )-\left [ p\left ( t-T_P \right )-p\left ( t-2T_P \right ) \right ]$$
$$ \Rightarrow r\left ( t \right )=p\left ( t \right )-2p\left ( t-T_P \right )+p\left ( t-2T_P \right )\:\:\:\:\:公式\:12$$
雙延遲線抵消器的優點是它可以廣泛地抑制雜波。兩個級聯的延遲線抵消器的輸出將等於單個延遲線抵消器輸出的平方。
因此,存在於MTI雷達接收器中的雙延遲線抵消器的輸出幅度將等於 $4A^2\left ( \sin\left [ \pi f_dT_P \right ] \right )^2$。
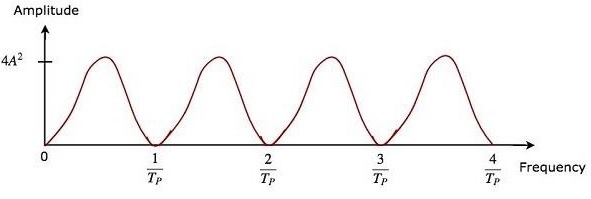
雙延遲線抵消器和兩個延遲線抵消器級聯組合的頻率響應特性相同。時域延遲線抵消器的優點是它可以在所有頻率範圍內工作。