雷達系統 - 概述

雷達是一種基於電磁波的探測系統，它透過輻射電磁波並研究回波或反射回的波來工作。

雷達的全稱是無線電探測和測距。探測是指目標是否存在。目標可以是靜止的或移動的，即非靜止的。測距是指雷達與目標之間的距離。

雷達可用於地面、海上和太空的各種應用。雷達的應用如下所示。

在任何雷達應用中，基本原理都保持不變。現在讓我們討論雷達的原理。

雷達的基本原理

雷達用於檢測物體並找到它們的位置。我們可以從下圖瞭解雷達的基本原理。

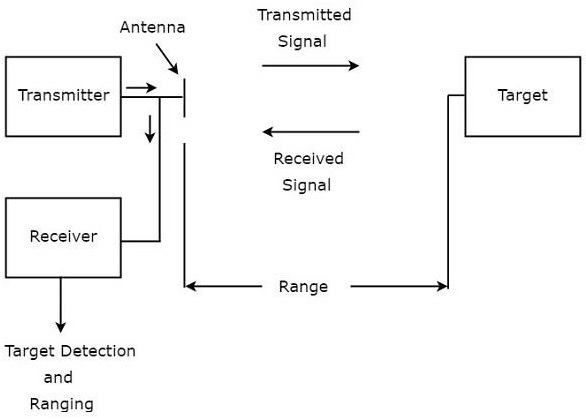
如圖所示，雷達主要由發射機和接收機組成。它使用相同的天線來發射和接收訊號。發射機的功能是將雷達訊號發射到目標所在的方向。

目標將接收到的訊號反射到各個方向。反射回天線的訊號被接收機接收。

以下是一些在本教程中很有用的基本術語。

現在，讓我們逐一討論這些基本術語。

雷達與目標之間的距離稱為目標的距離或簡稱為距離R。我們知道雷達向目標發射訊號，並且目標相應地以光速C向雷達傳送回波訊號。

設訊號從雷達傳播到目標再返回雷達所需的時間為'T'。雷達與目標之間的雙程距離將為2R，因為雷達與目標之間的距離為R。

現在，以下是速度的公式。

$$速度= \frac{距離}{時間}$$

$$\Rightarrow 距離=速度\times 時間$$

$$\Rightarrow 2R=C\times T$$

$$R=\frac{CT}{2}\:\:\:\:\:公式1$$

透過在公式1中代入C和T的值，我們可以找到目標的距離。

雷達訊號應在每個時鐘脈衝時發射。兩個時鐘脈衝之間的時間間隔應適當選擇，以便在下一個時鐘脈衝之前接收到對應於當前時鐘脈衝的回波訊號。下圖顯示了一個典型的雷達波形。

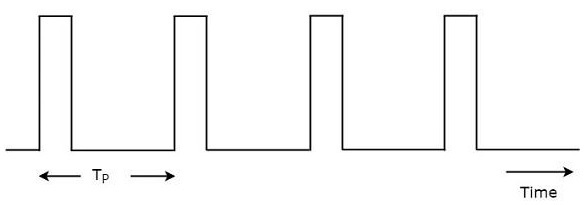
如圖所示，雷達發射週期性訊號。它具有一系列窄矩形脈衝。連續時鐘脈衝之間的時間間隔稱為脈衝重複時間，$T_P$。

脈衝重複時間的倒數稱為脈衝重複頻率，$f_P$。在數學上，它可以表示為

$$f_P=\frac{1}{T_P}\:\:\:\:\:公式2$$

因此，脈衝重複頻率只不過是雷達發射訊號的頻率。

我們知道雷達訊號應在每個時鐘脈衝時發射。如果我們選擇兩個時鐘脈衝之間較短的持續時間，則對應於當前時鐘脈衝的回波訊號將在下一個時鐘脈衝之後接收。由於此原因，目標的距離看起來比實際距離小。

因此，我們必須選擇兩個時鐘脈衝之間的時間間隔，以便在下一個時鐘脈衝開始之前接收對應於當前時鐘脈衝的回波訊號。然後，我們將獲得目標的真實距離，它也稱為目標的最大無模糊距離或簡稱為最大無模糊距離。

在公式1中代入$R=R_{un}$和$T=T_P$。

$$R_{un}=\frac{CT_P}{2}\:\:\:\:\:公式3$$

從公式2，我們將得到脈衝重複時間$T_P$作為脈衝重複頻率$f_P$的倒數。數學上，它可以表示為

$$T_P=\frac{1}{f_P}\:\:\:\:\:公式4$$

將公式4代入公式3。

$$R_{un}=\frac{C\left ( \frac{1}{f_P} \right )}{2}$$

$$R_{un}=\frac{C}{2f_P}\:\:\:\:\:公式5$$

我們可以使用公式3或公式5來計算目標的最大無模糊距離。

當我們將訊號從雷達發射後回波訊號在雷達處接收所需的時間考慮為脈衝寬度時，我們將獲得目標的最小距離。它也稱為目標的最短距離。

在公式1中代入$R=R_{min}$和$T=\tau$。

$$R_{min}=\frac{C\tau}{2}\:\:\:\:\:公式6$$

透過在公式6中代入C和$\tau$的值，我們將獲得目標的最小距離$R_{min}$的值。

列印頁面