
雷達系統 - 相控陣天線
單個天線可以在特定方向輻射一定量的功率。顯然,當我們將一組天線組合在一起使用時,輻射功率會增加。天線組稱為天線陣列。
天線陣列是一個由輻射器和元件組成的輻射系統。每個輻射器都有其自己的感應場。元件放置得非常靠近,以至於每個元件都位於相鄰元件的感應場中。因此,它們產生的輻射圖案將是各個輻射圖案的向量和。
天線單獨輻射,而在陣列中,所有元件的輻射相加形成輻射波束,該波束具有高增益、高方向性和更好的效能,並且損耗最小。
如果輻射圖案的形狀和方向取決於該陣列中每個天線的電流的相對相位和幅度,則稱天線陣列為相控天線陣列。
輻射方向圖
讓我們考慮“n”個各向同性輻射元件,當它們組合在一起時形成一個陣列。下圖將幫助您理解這一點。讓連續元件之間的間距為“d”個單位。
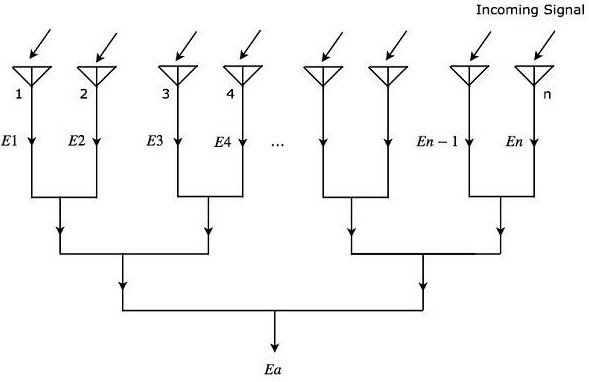
如圖所示,所有輻射元件都接收相同的入射訊號。因此,每個元件產生相等的輸出電壓 $sin \left ( \omega t \right)$。但是,相鄰元件之間將存在相等的相位差 $\Psi$。數學上,可以寫成 -
$$\Psi=\frac{2\pi d\sin\theta }{\lambda }\:\:\:\:\:公式\:1$$
其中,
$\theta$ 是入射訊號入射到每個輻射元件上的角度。
數學上,我們可以將“n”個輻射元件的輸出電壓表示式分別寫成
$$E_1=\sin\left [ \omega t \right]$$
$$E_2=\sin\left [\omega t+\Psi\right]$$
$$E_3=\sin\left [\omega t+2\Psi\right]$$
$$.$$
$$.$$
$$.$$
$$E_n=\sin\left [\omega t+\left (N-1\right )\Psi\right]$$
其中,
$E_1, E_2, E_3, …, E_n$ 分別是第一、第二、第三、…、第 n 個輻射元件的輸出電壓。
$\omega$ 是訊號的角頻率。
我們將透過新增陣列中每個元件的輸出電壓來獲得陣列的總輸出電壓 $E_a$,因為所有這些輻射元件都連線線上性陣列中。數學上,它可以表示為 -
$$E_a=E_1+E_2+E_3+ …+E_n \:\:\:公式\:2$$
代入公式 2 中 $E_1, E_2, E_3, …, E_n$ 的值。
$$E_a=\sin\left [ \omega t \right]+\sin\left [\omega t+\Psi\right ]+\sin\left [\omega t+2\Psi\right ]+\sin\left [\omega t+\left (n-1\right )\Psi\right]$$
$$\Rightarrow E_a=\sin\left [\omega t+\frac{(n-1)\Psi)}{2}\right ]\frac{\sin\left [\frac{n\Psi}{2}\right]}{\sin\left [\frac{\Psi}{2}\right ]}\:\:\:\:\:公式\:3$$
在公式 3 中,有兩個項。從第一項,我們可以觀察到總輸出電壓 $E_a$ 是一個具有角頻率 $\omega$ 的正弦波。但是,它具有 $\left (n−1\right )\Psi/2$ 的相移。公式 3 的第二項是幅度因子。
公式 3 的大小將為
$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\Psi}{2}\right ]}{\sin\left [\frac{\Psi}{2}\right]} \right |\:\:\:\:\:公式\:4$$
我們將透過將公式 1 代入公式 4 中得到以下公式。
$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right]}{\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]} \right |\:\:\:\:\:公式\:5$$
公式 5 稱為場強方向圖。當公式 5 的分子為零時,場強方向圖將具有零值
$$\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right ]=0$$
$$\Rightarrow \frac{n\pi d\sin\theta}{\lambda}=\pm m\pi$$
$$\Rightarrow nd\sin\theta=\pm m\lambda$$
$$\Rightarrow \sin\theta=\pm \frac{m\lambda}{nd}$$
其中,
$m$ 是一個整數,等於 1、2、3 等。
當公式 5 的分子和分母都等於零時,我們可以使用洛必達法則找到場強方向圖的最大值。我們可以觀察到,如果公式 5 的分母變為零,那麼公式 5 的分子也將變為零。
現在,讓我們得到公式 5 的分母變為零的條件。
$$\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]=0$$
$$\Rightarrow \frac{\pi d\sin\theta}{\lambda}=\pm p\pi$$
$$\Rightarrow d\sin\theta=\pm p\lambda$$
$$\Rightarrow \sin\theta=\pm \frac{p\lambda}{d}$$
其中,
$p$ 是一個整數,等於 0、1、2、3 等。
如果我們將 $p$ 視為零,那麼我們將得到 $\sin\theta$ 的值為零。對於這種情況,我們將得到對應於主瓣的場強方向圖的最大值。當我們考慮 $p$ 的其他值時,我們將得到對應於旁瓣的場強方向圖的最大值。
可以透過改變每個天線上存在的電流的相對相位來控制相控陣的輻射方向圖方向。這是電子掃描相控陣的優點。