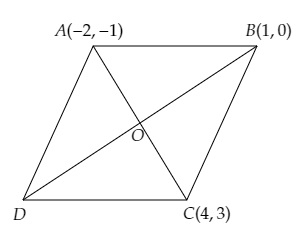
平行四邊形的三個連續頂點為(-2, -1)、(1, 0)和(4, 3)。求第四個頂點。

已知

平行四邊形的三個連續頂點為(-2, -1)、(1, 0)和(4, 3)。

要求

我們必須找到第四個頂點。

解答

設三個頂點的座標為A(-2, -1)、B(1, 0)和C(4, 3)。
設第四個頂點為D(x,y)，對角線AC和BD互相平分於點O。

這意味著，

O是AC的中點。

O的座標為(-2+4)/2, (-1+3)/2)

= (2/2, 2/2)

\( =(1,1) \)

O是BD的中點。

O的座標為((1+x)/2, (0+y)/2)

因此，

(1,1) = ((1+x)/2, y/2)

比較可得，

(1+x)/2 = 1

1+x = 1(2)

x = 2-1 = 1

類似地，

y/2 = 1

y = 1(2)

y = 2

因此，第四個頂點的座標為(1,2)。

Tutorialspoint

更新於：2022年10月10日

62 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習