梯子的底部距離牆壁6米,頂部到達離地面8米高的窗戶。如果移動梯子,使底部距離牆壁8米,那麼梯子的頂部會到達什麼高度?
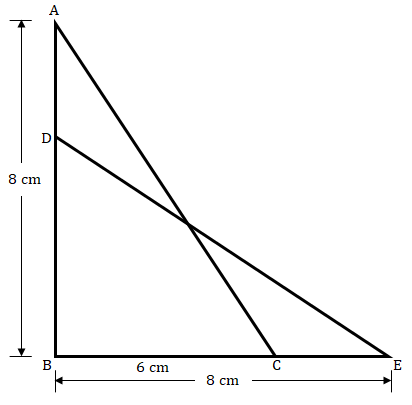
已知條件
梯子的底部距離牆壁6米,頂部到達離地面8米高的窗戶。
要求
我們需要求出當梯子移動後,底部距離牆壁8米時,頂部到達的高度。
解答
設梯子的長度為 $AC = DE = x\ 米$。
在直角三角形 $∆ABC$ 中,
根據勾股定理
$AC^2 = AB^2 + BC^2$
$x^2 = 8^2 + 6^2$
$x^2=64+36=100$
在直角三角形 $∆DBE$ 中,
根據勾股定理,
$DE^2 = DB^2 + BE^2$
$x^2 = DB^2 + 8^2$
$DB^2=x^2-64$
$DB^2 = 100 -64$ (因為 $x^2=100$)
$DB^2 = 36$
$DB = \sqrt{36}\ 米$
$DB = 6\ 米$
因此,梯子的頂部到達的高度為6米。

廣告

 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP