一根 25 米長的梯子靠在一面垂直的牆上，梯子的底部距離牆腳 7 米。如果梯子的頂部向下滑動 4 米，那麼梯子的底部會滑動多少距離？

已知

一根 25 米長的梯子靠在一面垂直的牆上，梯子的底部距離牆腳 7 米。

梯子的頂部向下滑動 4 米。

要求

我們需要找到梯子的底部滑動的距離。

解答

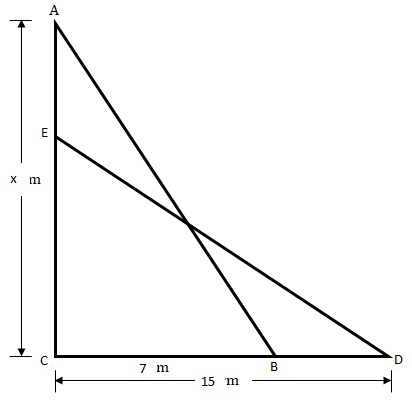
設梯子的長度為 $AB = DE = 25\ m$。

在 $\triangle ABC$ 中，

根據勾股定理

$AB^2 = AC^2 + BC^2$

$25^2 = 7^2 + x^2$

$x^2=625-49=576$

$x=\sqrt{576}=24$

在 $\triangle DEC$ 中，

根據勾股定理，

$DE^2 = DC^2 + CE^2$

$25^2 = DC^2 + (x-4)^2$

$DC^2=625-(24-4)^2$

$DC^2 = 625-400$   (因為 $20^2=400$)

$DC^2 = 225$

$DC = \sqrt{225}\ m$

$DC = 15\ m$

梯子底部滑動的距離為 $(15-7)\ m=8\ m$

因此，梯子的底部會滑動 $8\ m$。 

Tutorialspoint

更新時間： 2022年10月10日

107 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習