資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
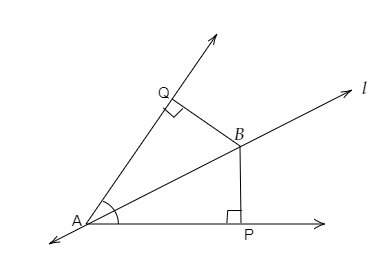
法律研究直線\( l \)是角\( A \)的角平分線，\( B \)是\( l \)上的任意一點。BP 和 BQ 是從 B 到角\( \angle A \)的兩邊的垂線。
(i) \( \triangle \mathrm{APB} \cong \triangle \mathrm{AQB} \)
(ii) \( \mathrm{BP}=\mathrm{BQ} \) 或 \( \mathrm{B} \)到角\( \mathrm{A} \)的兩邊的距離相等
已知
\( l \)是\( \angle A \)的角平分線，$B$是\( l \)上的一點。BP 和 BQ 是從 $B$ 到 $\angle A$ 兩邊的垂線。
要證明
\( \angle P A B=\angle Q A B \).......(i)
\( \angle \mathrm{APB}=\angle \mathrm{AQB}=90^{\circ} \)...........(ii)
在 \( \triangle \mathrm{APB} \) 和 \( \triangle \mathrm{AQB} \) 中，
$\angle P A B=\angle Q A B$
$\angle \mathrm{APB}=\angle \mathrm{AQB}$
$A B=A B$ (公共邊)
因此，根據 AAS 全等，
$\triangle \mathrm{APB} \cong \triangle \mathrm{AQB}$
這意味著，
$\mathrm{BP}=\mathrm{BQ}$ (CPCT)
證畢。
更新於: 2022年10月10日
61 次瀏覽
廣告