如圖所示，兩條直線\( \mathrm{AB} \& \mathrm{CD} \)相交於\( \mathrm{O} \)。如果\( \angle \mathrm{COT}=60^{\circ} \)，求\( \mathrm{a}, \mathrm{b}, \mathrm{c} \)。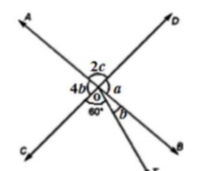"\n

已知

兩條直線\( \mathrm{AB} \& \mathrm{CD} \)相交於\( \mathrm{O} \)。

\( \angle \mathrm{COT}=60^{\circ} \)，
要求：

我們需要求出\( \mathrm{a}, \mathrm{b}, \mathrm{c} \)。

解答

我們知道，

對頂角相等。

一條直線上的角的和為$180^o$。

一個點周圍的角的和為$360^o$。
因此，

$a=4b$....(i)

$4b+60^o+b=180^o$

$\Rightarrow 5b=180^o-60^o$

$\Rightarrow 5b=120^o$

$\Rightarrow b=\frac{120^o}{5}$

$\Rightarrow b=24^o$

$a=4(24^o)$

$=96^o$

$4b+2c=180^o$

$4(24^o)+2c=180^o$

$96^o+2c=180^o$

$2c=180^o-96^o$

$2c=84^o$

$c=\frac{84^o}{2}$

$c=42^o$

因此，$\mathrm{a}=96^o, \mathrm{b}=24^o, \mathrm{c}=42^o$。

教程點

更新於: 2022年10月10日

1K+ 瀏覽量

開啟你的職業生涯

透過完成課程獲得認證

開始學習