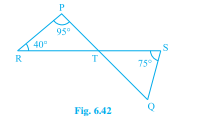
如圖 6.42 所示，如果直線\( \mathrm{PQ} \)和\( \mathrm{RS} \)相交於點\( \mathrm{T} \)，使得\( \angle \mathrm{PRT}=40^{\circ}, \angle \mathrm{RPT}=95^{\circ} \)且\( \angle \mathrm{TSQ}=75^{\circ} \)，求\( \angle \mathrm{SQT} \)。
"\n

已知

直線 $PQ$ 和 $RS$ 相交於點 $T$，使得 $\angle PRT=40^o, \angle RPT=95^o$ 且 $\angle TSQ=75^o$。

要求

求 $\angle SQT$。

解答

考慮 $\triangle PRT$。

我們知道，

三角形內角和始終為 $180^o$。

因此，

$\angle PRT+\angle RPT+\angle PTR=180^o$

將 $\angle PRT$ 和 $\angle RPT$ 的值代入上式，得到：

$95^o+40^o+\angle PTR=180^o$

$135^o+\angle PTR=180^o$

這意味著，

$\angle PTR=180^o-135^o$

$\angle PTR=45^o$

我們知道，

在三角形中，對頂角始終相等。

這意味著，

$\angle PTR=\angle STQ$

$\angle STQ=45^o$

由於三角形內角和始終為 $180^o$，我們得到：

$\angle TSQ+\angle PTR+\angle SQT=180^o$

代入數值，得到：

$75^o+45^o+\angle SQT=180^o$

$120^o+\angle SQT=180^o$

這意味著，

$\angle SQT=180^o-120^o$

$\angle SQT=60^o$

因此，$\angle SQT=60^o$。

教程點

更新時間： 2022 年 10 月 10 日

67 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習