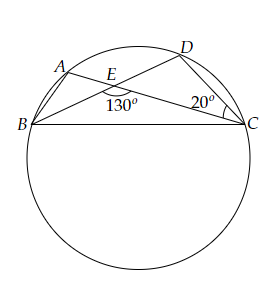
在下圖中，A、B、C和D是圓上的四個點。AC和BD相交於點E，使得∠BEC=130°且∠ECD=20°。求∠BAC。

已知

A、B、C和D是圓上的四個點。AC和BD相交於點E，使得∠BEC=130°且∠ECD=20°。
要求：

求∠BAC。

解答

我們知道：

圓周角相等。

這意味著：

∠BAC = ∠CDE

∠CEB = ∠CDE + ∠ECD (外角性質)

130° = ∠CDE + 20°

∠CDE = 130° - 20°

= 110°

因此：

∠BAC = ∠CDE = 110°

因此，∠BAC = 110°。

教程點

更新於：2022年10月10日

瀏覽量：35

開啟你的職業生涯

完成課程獲得認證

開始學習