資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學如圖 6.40，∠X = 62°，∠XYZ = 54°。如果 YO 和 ZO 分別是△XYZ 中∠XYZ 和∠XZY 的平分線，求∠OZY 和∠YOZ。
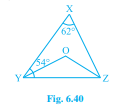
已知
∠X = 62°，∠XYZ = 54°。
YO 和 ZO 分別是△XYZ 中∠XYZ 和∠XZY 的平分線。
求解
我們需要求出∠OZY 和∠YOZ。
解答
我們知道三角形內角和始終為 180°。
這意味著：
∠X + ∠XYZ + ∠XZY = 180°
代入 X 和 Y 的值，我們得到：
62° + 54° + ∠XZY = 180°
這意味著：
116° + ∠XZY = 180°
∠XZY = 180° - 116°
∠XZY = 64°
我們知道：
YO 和 ZO 分別是△XYZ 中∠XYZ 和∠XZY 的平分線
因此我們得到：
∠OYZ = 1/2∠XYZ
∠OYZ = 54°/2
∠OYZ = 27°
同樣地，我們得到：
∠OZY = 1/2∠XZY
∠OZY = 64°/2
∠OZY = 32°
由於我們知道三角形內角和始終為 180°，我們得到：
∠OZY + ∠OYZ + ∠O = 180°
代入數值，我們得到：
32° + 27° + ∠O = 180°
59° + ∠O = 180°
∠O = 180° - 59°
∠O = 121°
因此，∠OZY = 32°，∠YOZ = 27°。(注意原文計算結果有誤，∠YOZ應為121°)
更新於：2022年10月10日
瀏覽量：38
廣告