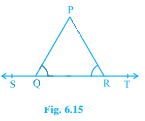
如圖6.15所示，∠PQR=∠PRQ，證明∠PQS=∠PRT

已知

∠PQR=∠PRQ。

要求

我們必須證明∠PQS=∠PRT。

解答

SQRT是一條直線。

我們知道：

線性對角的度數之和總是180°。

∠PQS+∠PQR=180° (因為它們是線性對)

∠PRT+∠PRQ=180° (因為它們是線性對)

因此：

∠PQR=180°-∠PQS …(i)

∠PRQ=180°-∠PRT …(ii)

因為：

∠PQR=∠PRQ

透過等式，我們得到：

180°-∠PQS=180°-∠PRT

這意味著：

∠PQS=∠PRT。

教程點

更新於：2022年10月10日

60次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習