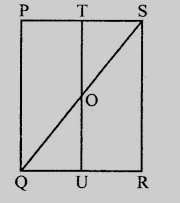
如圖所示，$PQRS$是一個正方形，$T$和$U$分別是$PS$和$QR$的中點。如果$PQ = 8\ cm$，求$\triangle OTS$的面積。
"\n

已知

$PQRS$是一個正方形，$T$和$U$分別是$PS$和$QR$的中點。

要求

如果$PQ = 8\ cm$，我們需要求$\triangle OTS$的面積。

解答

$T$和$U$分別是邊$PS$和$QR$的中點。

這意味著，

$TU \parallel PQ, TO \parallel PQ$

在$\triangle RQS$中，

$T$是$PS$的中點，且$TO \parallel PQ$

$O$是$SQ$的中點

$\mathrm{TO}=\frac{1}{2} \mathrm{PQ}$

$=\frac{1}{2} \times 8$

$=4 \mathrm{~cm}$

$\mathrm{TS}=\frac{1}{2} \times \mathrm{PS}$

$=\frac{1}{2} \times 8$

$=4 \mathrm{~cm}$

$\Delta \mathrm{OTS}$的面積$=\frac{1}{2} \mathrm{OT} \times \mathrm{TS}$

$=\frac{1}{2} \times 4 \times 4$

$=8 \mathrm{~cm}^{2}$

$\triangle OTS$的面積是$8\ cm^2$。

教程點

更新於: 2022年10月10日

39 次檢視

開啟你的職業生涯

透過完成課程獲得認證

開始學習