資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學如圖5所示，三角形PQR外接一個半徑為6釐米的圓，圓與QR相切於點T，QT和TR的長度分別為12釐米和9釐米。如果△PQR的面積為189平方釐米，求PQ和PR的長度。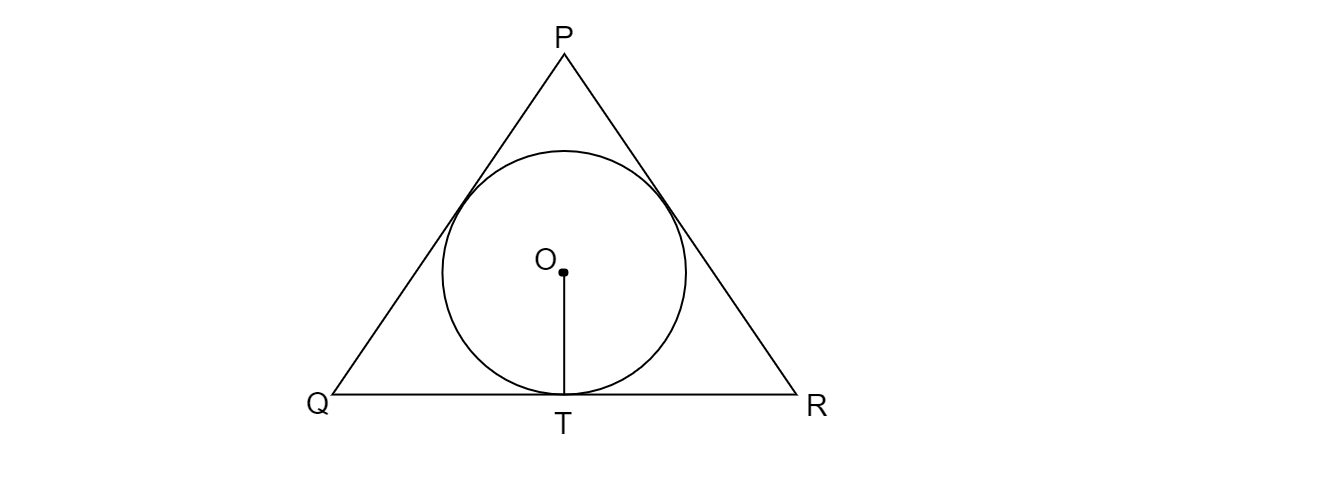
已知：一個以O為圓心，半徑為6釐米的圓，三角形PQR外接該圓，T為切點，且將QR分成QT=12釐米和TR=9釐米兩段。三角形的面積=189平方釐米。
求解：求PQ和PR的長度。
解
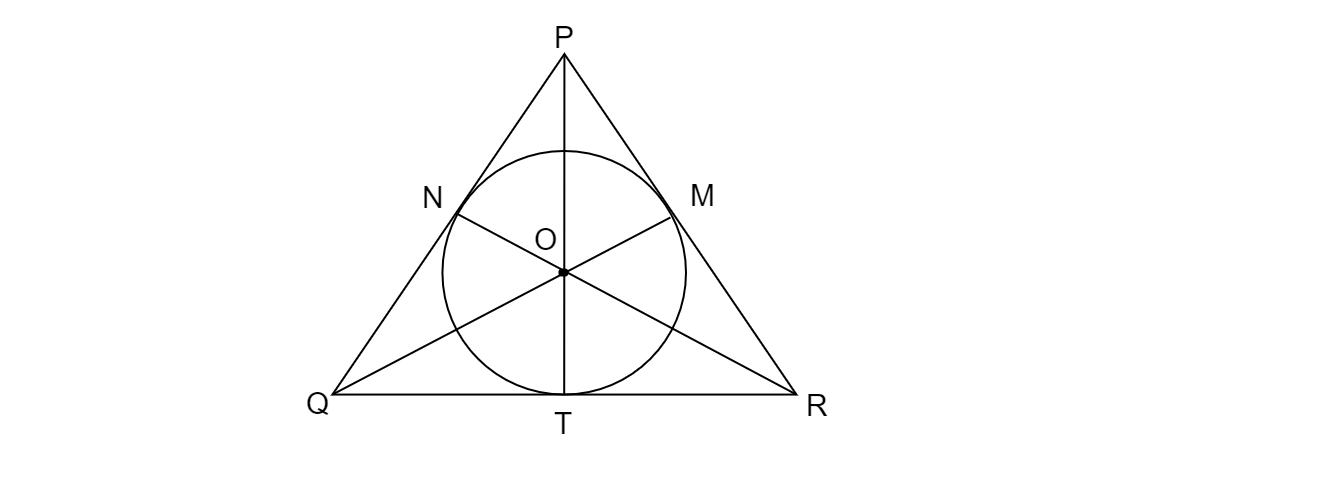
連線OP、OM、ON、OQ和OR。
PQ=PN+QN
PR=PM+MR
由於PQ和PR是圓的切線，所以PN=PM，QN=QT，MR=TR
已知三角形的面積=189平方釐米
三角形△PQR的底邊為：
QR=QT+TR=12+9=21釐米
我們知道三角形的面積公式為：
=½ × 底 × 高
189=½ × 21 × PT
⇒ PT=(189 × 2) / 21
=18釐米
我們知道PT=PO+OT
⇒ PO=PT-OT
=18-6 (因為OT是已知圓的半徑6釐米)
=12釐米
且ON=OT=OM=圓的半徑。
在三角形△PON中：
PN=√(OP² - ON²)
=√(12² - 6²)
=√(144-36)
=√108
=6√3
PQ=PN+QN=PN+QT=6√3+12≈22.40釐米
PR=PM+MR=PN+TR=6√3+9≈19.40釐米
因此，PQ和PR的長度分別約為22.40釐米和19.40釐米。
更新於：2022年10月10日
49次瀏覽
廣告