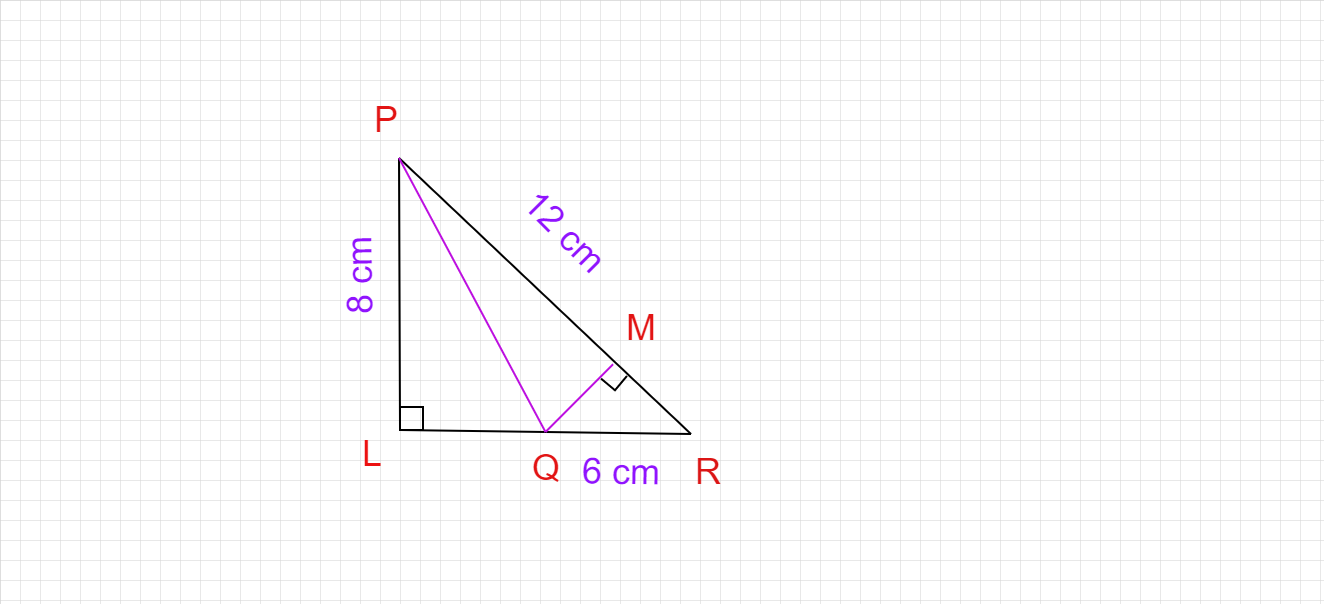
如圖所示，如果 $PR=12 cm, QR = 6 cm$ 且 $PL=8cm$，則求 $QM$。

"\n

已知

在給定圖形中，如果 $PR=12 cm, QR = 6 cm$ 且 $PL=8cm$。

要求

我們必須找到 $QM$ 的長度。

解

$\triangle PLR$ 是一個直角三角形。

根據勾股定理，

$PL^2+LR^2=PR^2$

$8^2+LR^2=12^2$

$64+LR^2=144$

$LR^2=144-64=80$

$LR=\sqrt{80}$

$LR=4\sqrt{5}$

$LR = LQ+QR$

$LQ=LR-QR$

$LQ=4\sqrt{5}-6$

我們知道三角形的面積是 $\frac{1}{2} \times b \times h$

所以，$\triangle PLR$ 的面積 = $\frac{1}{2} \times LR \times PL$

                                                 $ = \frac{1}{2} \times 4\sqrt{5}  \times 8$

                                                 $ = 16\sqrt{5} cm^2$.

$\triangle PLQ$ 的面積 = $\frac{1}{2} \times LQ \times PL$

                                                 $ = \frac{1}{2} \times (4\sqrt{5}-6) \times 8$

                                                 $= 4(4\sqrt{5}-6)$

                                                 $ = 16\sqrt{5} -24 cm^2$.

$\triangle PQR$ 的面積 =  $\frac{1}{2} \times PR \times QM$

這裡，$\triangle PQR$ 的面積 = $\triangle PLR$ 的面積 - $\triangle PLQ$ 的面積     

           $\triangle PQR$ 的面積 =  $16\sqrt{5} cm^2 - (16\sqrt{5} -24 )cm^2$

                                         $ = 16\sqrt{5} cm^2 - 16\sqrt{5} +24 cm^2$

              $\triangle PQR$ 的面積 =24 cm^2。

$\frac{1}{2} \times PR \times QM = 24$

$\frac{1}{2} \times 12 \times QM = 24$

$6 \times QM = 24 $

$QM = \frac{24}{6} = 4$

因此，$QM$ 的長度為 4 cm。

教程點

更新於: 2022年10月10日

62 次瀏覽

開啟您的 職業生涯

透過完成課程獲得認證

開始學習