在給定圖形中，$PQRS$ 是一個平行四邊形，其對角線 $PR$ 和 $SQ$ 相交於點 $O$。$OR=7.5\ cm$，$SQ$ 比 $PR$ 短 $5\ cm$，求 $OS$。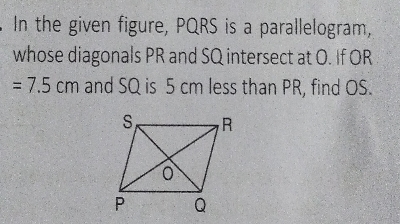"\n

已知：在給定圖形中，$PQRS$ 是一個平行四邊形，其對角線 $PR$ 和 $SQ$ 相交於點 $O$。$OR=7.5\ cm$，$SQ$ 比 $PR$ 短 $5\ cm$。

求解：求 $OS$。

解答

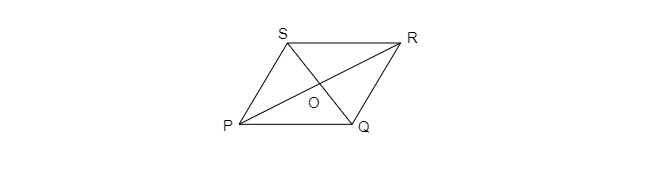
$\because$ 在平行四邊形中，對角線互相平分。

$OR=7.5$，則 $OP$ 也將等於 $7.5$。

因此，$PR=7.5+7.5=15\ cm$

由於 $SQ=PR-5$

$\Rightarrow SQ=15-5=10\ cm$

$\Rightarrow OQ=OS=\frac{SQ}{2}=5\ cm$

Tutorialspoint

更新於： 2022年10月10日

153 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

開始學習