如圖所示，點A、B、C和D是四個圓的圓心，每個圓的半徑為一個單位長度。如果從正方形ABCD內部隨機選擇一個點，那麼該點被選自陰影區域的機率是多少？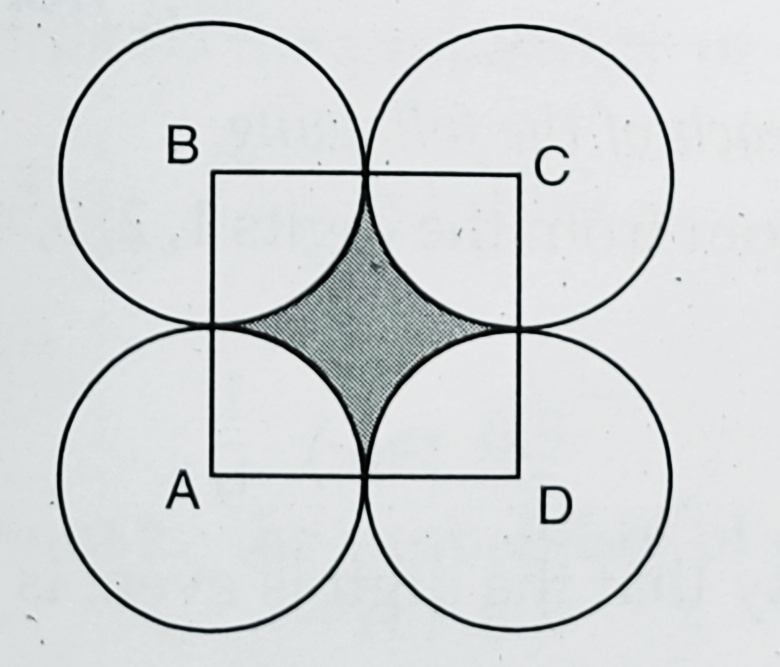

已知

如圖所示，點A、B、C和D是四個圓的圓心，每個圓的半徑為一個單位長度。

從正方形ABCD內部隨機選擇一個點。

要求

我們必須找到該點被選自陰影區域的機率。

解答

每個圓的半徑 = 1 個單位

這意味著：

正方形ABCD的邊長 = 1 + 1 = 2 個單位。

正方形的面積 = 2² = 4 平方單位。

正方形內A、B、C和D處的四個象限的面積 = 4 × (1/4)πr²

= π(1)²

= π 平方單位

這意味著：

陰影區域的面積 = 4 - π 平方單位

因此：

該點被選自陰影區域的機率 = 陰影區域的面積 / 正方形的面積

= (4 - π) / 4

= 1 - π/4

該點被選自陰影區域的機率是 1 - π/4。

Tutorialspoint

更新於：2022年10月10日

瀏覽量：151

開啟你的職業生涯

完成課程獲得認證

開始學習