資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學在下圖中，\( AB=36 \mathrm{~cm} \) ，\( M \) 是 \( AB \) 的中點。在 \( AB \)、\( AM \) 和 \( MB \) 上分別以其為直徑作半圓。以 \( C \) 為圓心的圓與這三個圓都相切。
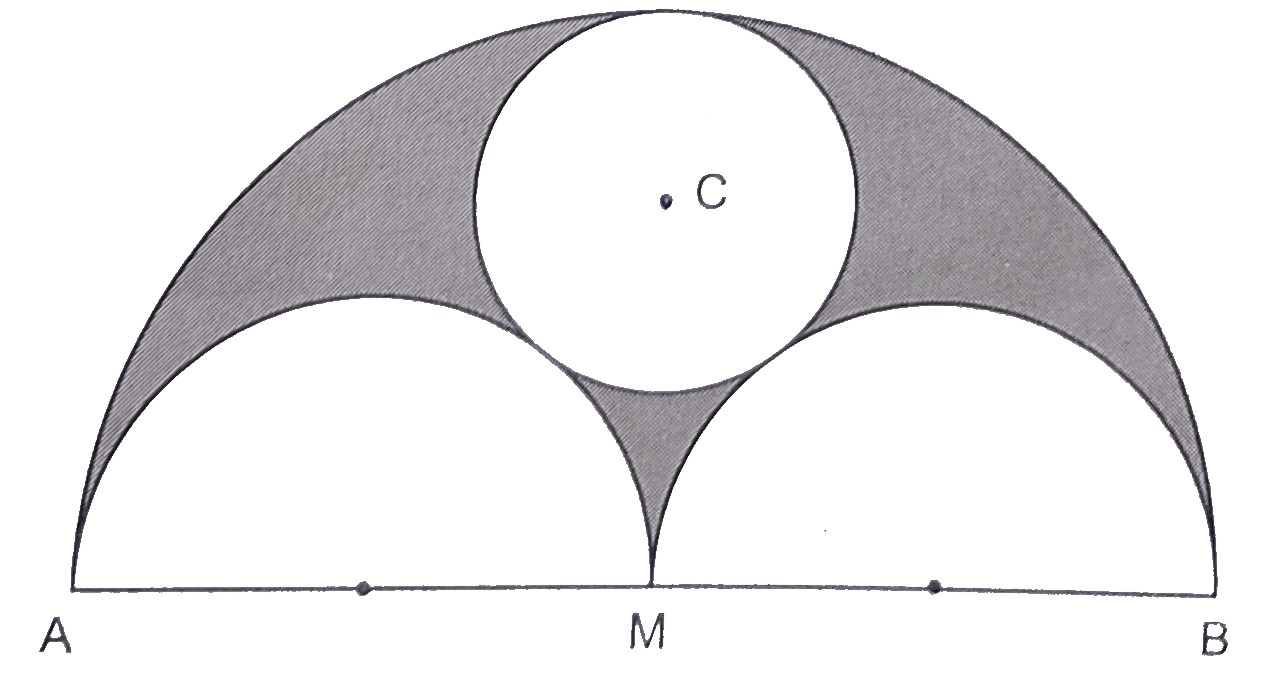
已知
\( AB=36 \mathrm{~cm} \) ，\( M \) 是 \( AB \) 的中點。
在 \( AB \)、\( AM \) 和 \( MB \) 上分別以其為直徑作半圓。
以 \( C \) 為圓心的圓與這三個圓都相切。
要求：
求陰影部分的面積。
解答
最大半圓的直徑 = 36 cm
這意味著：
半徑 \(R =\frac{36}{2}\)
\(= 18\ cm\)
每個較小半圓的直徑 = 18 cm
這意味著：
半徑 \(r_{1}=\frac{18}{2}\)
\(=9 \mathrm{~cm}\)
最小圓的直徑 \(=\frac{1}{3} \times 36\)
\(=12 \mathrm{~cm}\)
這意味著：
半徑 \(r_{2}=\frac{12}{2}\)
\(=6 \mathrm{~cm}\)
因此：
陰影部分的面積 = 最大半圓的面積 - (兩個較小半圓的面積 + 最小圓的面積)
\(=\frac{1}{2} \pi \mathrm{R}^{2}-(2 \times \frac{1}{2} \pi r_{1}^{2}+\pi r_{2}^{2})\)
\(=\frac{1}{2} \pi \mathrm{R}^{2}-(\pi r_{1}^{2}+\pi r_{2}^{2})\)
\(=\frac{1}{2} \pi \mathrm{R}^{2}-\pi r_{1}^{2}-\pi r_{2}{ }^{2}\)
\(=\pi[\frac{1}{2} \mathrm{R}^{2}-r_{1}^{2}-r_{2}^{2}]\)
\(=\pi[\frac{1}{2}(18)^{2}-(9)^{2}-(6)^{2}]\)
\(=\pi[\frac{324}{2}-81-36]\)
\(=\pi(\frac{324}{2}-117)\)
\(=\pi(162-117)\)
\(=45 \pi \mathrm{cm}^{2}\)
陰影部分的面積是 \(45 \pi\ cm^2\)。
45 次瀏覽
