資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
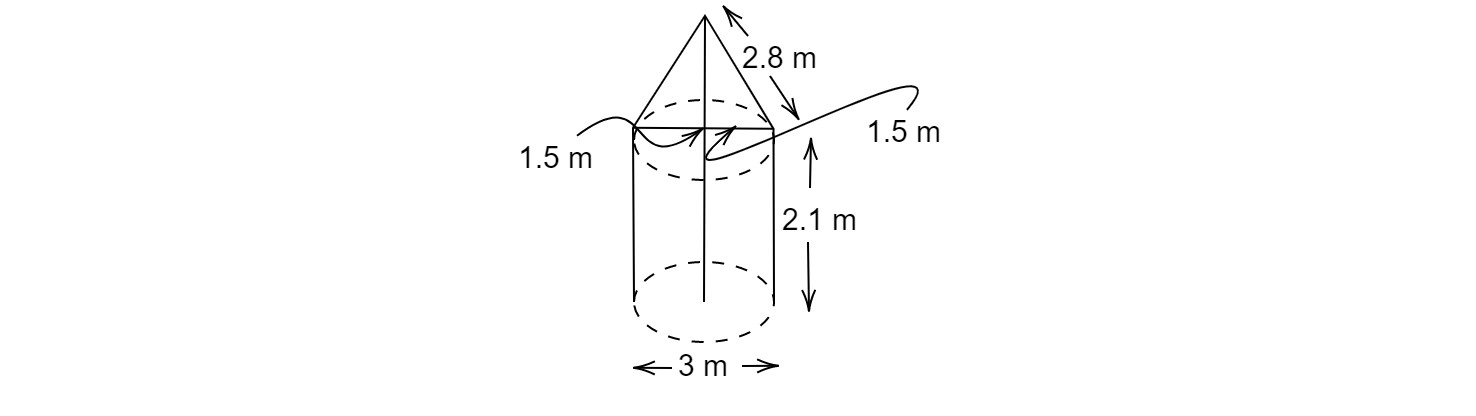
法律研究如圖所示，一個帳篷呈圓柱體形，頂部為圓錐形，且圓柱體和圓錐體的直徑相同。如果圓柱體部分的高度和直徑分別為 2.1 米和 3 米，圓錐體部分的斜高為 2.8 米，求製作該帳篷所需的帆布成本，已知帆布的價格為每平方米 500 盧比。
"\n
已知：一個帳篷呈圓柱體形，頂部為圓錐形，且圓柱體和圓錐體的直徑相同。如果圓柱體部分的高度和直徑分別為 $2.1\ m$ 和 $3\ m$，圓錐體部分的斜高為 $2.8\ m$。
求解：求製作該帳篷所需的帆布成本，已知帆布的價格為每平方米 500 盧比。
解答
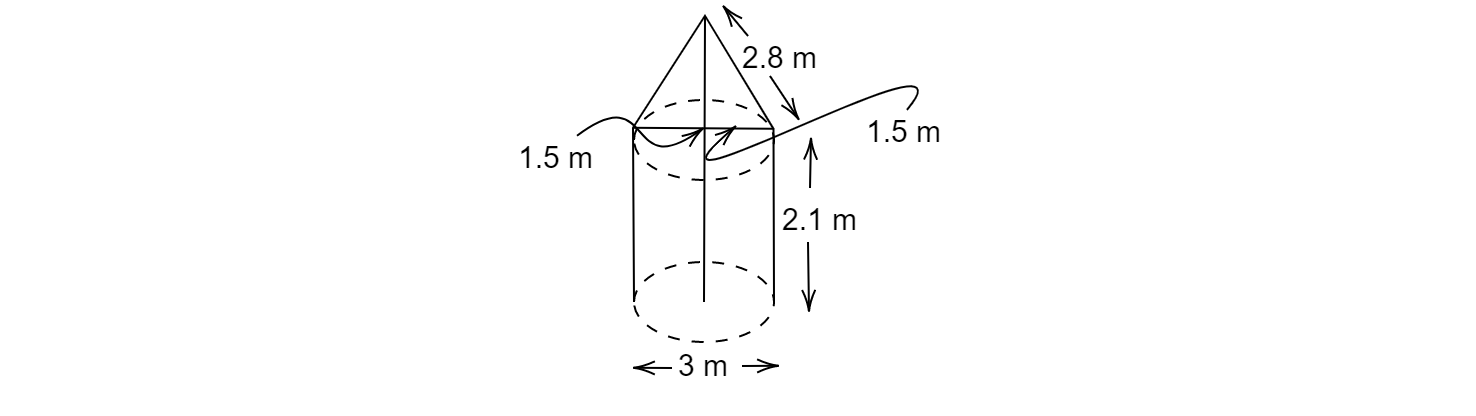
對於圓錐體部分，我們有
$r=1.5\ m$ 和 $l=2.8\ m$
$\therefore \ S_{1}=$圓錐體部分的側面積
$\therefore \ S_{1} \ =\ \pi rl$
$=\pi \times \ 1.5\ \times \ 2.8$
$=\ 4.2\pi \ m^{2}$
對於圓柱體部分，我們有
$r =1.5\ m$ 和 $h= 2.1\ m$
$\therefore \ S_{2} =$圓柱體部分的側面積
$\therefore \ S_{2} \ =\ 2\pi rh$
$=2 \times \pi \ \times \ 1.5\ \times \ 2.1$
$=6.3\pi \ m^{2}$
製作帳篷所需的帆布面積 $S_{1}+S_{2}=4.2\pi+6.3\pi=10.5\pi\ cm^{2}$
$=10.5\times \frac{22}{7}$
$33\ m^{2}$
帆布的總成本，每平方米 500 盧比 $=Rs.( 500\times33)=Rs.\ 16500$
更新於： 2022 年 10 月 10 日
89 次瀏覽
廣告