如果以三角形的兩條邊為直徑作圓，證明這兩個圓的交點位於第三條邊上。

已知

以三角形的兩條邊為直徑作圓。

要求

我們必須證明這兩個圓的交點位於第三條邊上。

解答

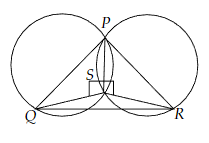
讓我們畫一個三角形$PQR$，以及兩個分別以$PQ$和$PR$為直徑的圓。

我們知道：

半圓中的圓周角都等於90度。

這意味著：

$\angle PSQ = \angle PSR = 90^o$

$\angle PSQ+\angle PSR = 180^o$

因此：

$\angle BDC$是一條直線。

所以，我們可以說$S$位於直線$QR$上。

證畢。

Tutorialspoint

更新於：2022年10月10日

139 次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習