利用基本比例定理（B.P.T.），證明過三角形一邊中點且平行於另一邊的直線平分第三邊。

待辦事項

我們必須證明過三角形一邊中點且平行於另一邊的直線平分第三邊。

解答

我們知道：

如果一條直線將三角形的兩邊按比例分割，那麼這條直線平行於第三邊。

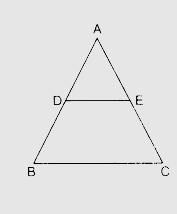
在△ABC中，D為AB的中點，且DE∥BC

在△ABC中，DE∥BC，

這意味著：

AD/DB = AE/EC .........(i)

AD = DB

這意味著：

AD/AD = AE/EC

1 = AE/EC

AE = EC

因此，DE平分AC

證畢。

教程點

更新於：2022年10月10日

97 次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習